Октаэдрическая симметрия

Эта статья включает в себя список общих ссылок , но он остается в основном непроверенным, поскольку в нем отсутствуют соответствующие встроенные ссылки . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Май 2013 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Группы точек в трех измерениях

Инволюционная симметрия C s , (*) [] =	Циклическая симметрия C nv , (* nn) [n] =	Диэдральная симметрия D nh , (* n22) [n, 2] =
Группа полиэдров , [n, 3], (* n32)
Тетраэдрическая симметрия T d , (* 332) [3,3] =	Октаэдрическая симметрия O h , (* 432) [4,3] =	Икосаэдрическая симметрия I h , (* 532) [5,3] =

График цикла
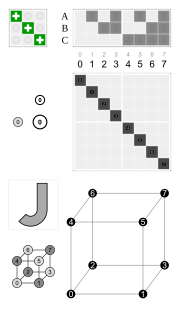
Четыре шестиугольных цикла имеют общую инверсию (черный узел наверху). Шестиугольники симметричны, поэтому, например, 3 и 4 находятся в одном цикле.

Правильный октаэдр имеет 24 симметрии вращения (или сохраняющие ориентацию) и 48 симметрий в целом. К ним относятся преобразования, сочетающие отражение и вращение. Куб имеет тот же набор симметрий, так как многогранник , который является двойным к октаэдру.

Группа сохраняющих ориентацию симметрий - это S ₄ , симметрическая группа или группа перестановок четырех объектов, поскольку существует ровно одна такая симметрия для каждой перестановки четырех пар противоположных граней октаэдра.

Подробности [ править ]

Киральная и полная (или ахиральная ) октаэдрическая симметрия - это дискретные точечные симметрии (или, что эквивалентно, симметрии на сфере ) с наибольшими группами симметрии, совместимыми с трансляционной симметрией . Они являются одними из кристаллографических точечных групп в кубической кристаллической системе .

Примеры
${\ displaystyle (0,0) = 0}$	${\ displaystyle (3,0) = 7}$	${\ displaystyle (0,3) = 3}$	${\ Displaystyle (7,1) = 1 '}$	${\ displaystyle (4,5) = 9 '}$
${\ displaystyle (7,0) = 0 '}$	${\ displaystyle (4,0) = 7 '}$	${\ Displaystyle (7,3) = 3 '}$	${\ Displaystyle (0,1) = 1}$	${\ Displaystyle (3,5) = 9}$
Полный список можно найти в статье Викиверситета .

Поскольку группа гипероктаэдра размерности 3, полная группа октаэдра является сплетением , и естественный способ идентифицировать ее элементы - это пары с и . Но поскольку это также прямое произведение , можно просто идентифицировать элементы тетраэдрической подгруппы T _d как и их инверсии как .${\ Displaystyle S_ {2} \ wr S_ {3} \ simeq S_ {2} ^ {3} \ rtimes S_ {3}}$
${\ Displaystyle (м, п)}$${\ displaystyle m \ in [0,2 ^ {3})}$${\ displaystyle n \ in [0,3!)}$
${\displaystyle S_{4}\times S_{2}}$${\displaystyle a\in [0,4!)}$${\displaystyle a'}$

Так, например, идентичность представлена ​​как, а инверсия - как . представлен как и как .${\displaystyle (0,0)}$${\displaystyle 0}$${\displaystyle (7,0)}$${\displaystyle 0'}$
${\displaystyle (3,1)}$${\displaystyle 6}$${\displaystyle (4,1)}$${\displaystyle 6'}$

Rotoreflection представляет собой сочетание вращения и отражения.

Иллюстрация вращающихся отражений
применяется при повороте на 120 ° ${\displaystyle 4}$ дает вращательное отражение 60 ° .${\displaystyle 8'}$ ${\displaystyle 7'\circ 4=8'}$
Отражение ${\displaystyle 7'}$ применяется при повороте на 90 ° ${\displaystyle 22'}$ дает вращательное отражение 90 ° .${\displaystyle 17}$ ${\displaystyle 7'\circ 22'=17}$

Хиральная октаэдрическая симметрия [ править ]

O , 432 или [4,3] ⁺ порядка 24, является хиральной октаэдрической симметрией или вращательной октаэдрической симметрией . Эта группа похожа на хиральную тетраэдрическую симметрию T , но оси C ₂ теперь являются осями C ₄ , и, кроме того, имеется 6 осей C ₂ , проходящих через средние точки ребер куба. T _d и O изоморфны как абстрактные группы: они обе соответствуют S ₄ , симметричной группе на 4 объектах. T _d - объединение Tи набор, полученный путем объединения каждого элемента O \ T с инверсией. O - группа вращения куба и правильного октаэдра .

Полная октаэдрическая симметрия [ править ]

O _h , * 432 , [4,3] или m3m порядка 48 - ахиральная октаэдрическая симметрия или полная октаэдрическая симметрия . Эта группа имеет те же оси вращения, что и O , но с зеркальными плоскостями, включающими обе зеркальные плоскости T _d и T _h . Эта группа изоморфна S ₄ . C ₂ , и является полной группой симметрии куба и октаэдра . Это группа гипероктаэдра при n = 3. См. Также изометрии куба .

С осями 4-го порядка в качестве координатных осей фундаментальная область O _h задается как 0 ≤ x ≤ y ≤ z . Объект с этой симметрией характеризуется частью объекта в фундаментальной области, например, куб задается как z = 1, а октаэдр - как x + y + z = 1 (или соответствующие неравенства, чтобы получить твердое тело вместо поверхности). ax + by + cz = 1 дает многогранник с 48 гранями, например додекаэдр дисьякиса.

Грани 8 на 8 объединяются в большие грани для a = b = 0 (куб) и 6 на 6 для a = b = c (октаэдр).

9 зеркальных линий полной октаэдрической симметрии можно разделить на две подгруппы 3 и 6 (нарисованные фиолетовым и красным), представляющие две ортогональные подсимметрии: D 2h и T d . Симметрию D _2h можно удвоить до D _4h , восстановив 2 зеркала из одной из трех ориентаций.

Октаэдрическая симметрия и отражающие подгруппы
Ортографическая проекция Стереографическая проекция 4-кратный 3-кратный 2-кратный О ч , [4,3],, полная октаэдрическая симметрия (3 + 6 зеркал) T d , [3,3] = [1 + , 4,3], знак равно , тетраэдрическая подгруппа (6 зеркал) C 3v , [3],, двугранная подгруппа (3 зеркала)	Ортографическая проекция Стереографическая проекция 4-кратный 3-кратный 2-кратный D 4h , [4,2], диэдральная подгруппа (1 + 2 + 2 зеркала) D 2h , [2,2] = [4,3 *], = диэдральная подгруппа (1 + 1 + 1 зеркала) C 4v , [4],, двугранная подгруппа (2 + 2 зеркала)

Матрицы вращения [ править ]

Возьмите набор всех матриц перестановок 3x3 и присвойте знак + или знак - каждой из трех единиц. Всего имеется 6 перестановок x 8 комбинаций знаков = 48 матриц, дающих полную группу октаэдра. Имеется ровно 24 матрицы с определителем = +1, и это матрицы вращения киральной октаэдрической группы. Остальные 24 матрицы соответствуют отражению или инверсии.

Для октаэдрической симметрии необходимы три отражающих матрицы генератора, которые представляют три зеркала диаграммы Кокстера-Дынкина . Продукт отражений производят 3 вращающихся генератора.

[4,3],

	Размышления			Вращения
Имя	R 0	R 1	R 2	R 0 R 1	R 1 R 2	R 0 R 2
Группа
Заказ	2	2	2	4	3	2
Матрица	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&1&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\0&0&1\\1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&-1\\\end{smallmatrix}}\right]}$

Подгруппы полной октаэдрической симметрии [ править ]

Schoe.	Coxeter		Сфера.	HM	Структура	Цикл.	Заказ	Индекс
О ч	[4,3]		* 432	м 3 м	S 4 × S 2		48	1
Т д	[3,3]		* 332	4 3 мес.	S 4		24	2
Д 4ч	[2,4]		* 224	4 / ммм	Dih 1 × Dih 4		16	3
Д 2ч	[2,2]		* 222	М-м-м	Dih 1 3 = Dih 1 × Dih 2		8	6
C 4v	[4]		* 44	4мм	Dih 4		8	6
C 3v	[3]		* 33	3м	Dih 3 = S 3		6	8
C 2v	[2]		* 22	мм2	Dih 2		4	12
C s = C 1v	[]		*	2 или м	Dih 1		2	24
Т ч	[ 3+ , 4]		3 * 2	м 3	А 4 × S 2		24	2
C 4ч	[ 4+ , 2]		4 *	4 / м	Z 4 × Dih 1		8	6
D 3d	[ 2+ , 6]		2 * 3	3 мес.	Dih 6 = Z 2 × Dih 3		12	4
D 2d	[ 2+ , 4]		2 * 2	4 2 мес.	Dih 4		8	6
C 2h = D 1d	[2 + , 2]		2 *	2 / м	Z 2 × Dih 1		4	12
S 6	[2 + , 6 + ]		3 ×	3	Z 6 = Z 2 × Z 3		6	8
S 4	[ 2+ , 4+ ]		2 ×	4	Z 4		4	12
S 2	[ 2+ , 2+ ]		×	1	S 2		2	24
О	[4,3] +		432	432	S 4		24	2
Т	[3,3] +		332	23	А 4		12	4
D 4	[2,4] +		224	422	Dih 4		8	6
D 3	[2,3] +		223	322	Dih 3 = S 3		6	8
D 2	[2,2] +		222	222	Dih 2 = Z 2 2		4	12
C 4	[4] +		44	4	Z 4		4	12
C 3	[3] +		33	3	Z 3 = A 3		3	16
C 2	[2] +		22	2	Z 2		2	24
C 1	[] +		11	1	Z 1		1	48

Изометрии куба [ править ]

Куб имеет 48 изометрий (элементов симметрии), образующих группу симметрии O _h , изоморфную S 4  ×  C ₂ . Их можно разделить на следующие категории:

• O (тождество и 23 собственных вращения) со следующими классами сопряженности (в скобках указаны перестановки диагоналей тела и представление единичного кватерниона ):
  • личность (личность; 1)
  • вращение вокруг оси от центра грани к центру противоположной грани на угол 90 °: 3 оси, по 2 на каждую ось, вместе 6 ((1 2 3 4) и т.д .; ((1 ±  i  ) / √ 2 и т. Д.)
  • то же самое на угол 180 °: 3 оси, по 1 на ось, вместе 3 ((1 2) (3 4) и т.д .; i , j , k )
  • вращение вокруг оси от центра кромки до центра противоположной кромки на угол 180 °: 6 осей, по 1 на каждую ось, вместе 6 ((1 2) и т.д .; (( i  ±  j  ) / √ 2 и др.)
  • вращение вокруг диагонали тела на угол 120 °: 4 оси, по 2 на каждую ось, вместе 8 ((1 2 3) и т.д .; (1 ±  i  ±  j  ±  k ) / 2)
• То же самое с инверсией ( x отображается в - x ) (также 24 изометрии). Обратите внимание, что поворот на угол 180 ° вокруг оси в сочетании с инверсией - это просто отражение в перпендикулярной плоскости. Комбинация инверсии и вращения вокруг диагонали тела на угол 120 ° представляет собой вращение вокруг диагонали тела на угол 60 ° в сочетании с отражением в перпендикулярной плоскости (само вращение не отображает куб сам на себя; пересечение плоскости отражения с кубом представляет собой правильный шестиугольник ).

Изометрию куба можно определить по-разному:

• гранями три заданные смежные грани (скажем, 1, 2 и 3 на кубике) отображаются в
• по изображению куба с несимметричной маркировкой на одной грани: грань с маркировкой, нормальная или зеркальная, и ориентация
• перестановкой четырех диагоналей тела (возможна каждая из 24 перестановок) в сочетании с переключателем для инверсии куба, или нет

Для кубиков с цветом или маркировкой (например, у кубиков ) группа симметрии является подгруппой O _h .

Примеры:

• C _{4 v} , [4], (* 422): если одна грань имеет другой цвет (или две противоположные грани имеют цвета, отличные друг от друга и от других четырех), куб имеет 8 изометрий, как квадрат в 2D. .
• D _{2 h} , [2,2], (* 222): если противоположные грани имеют одинаковые цвета, разные для каждого набора из двух, куб имеет 8 изометрий, как кубоид .
• D _{4 h} , [4,2], (* 422): если две противоположные грани одного цвета, а все остальные грани одного другого цвета, куб имеет 16 изометрий, как квадратная призма (квадратная коробка).
• C _{2 v} , [2], (* 22):
  • если две смежные грани одного цвета, а все остальные грани одного другого цвета, куб имеет 4 изометрии.
  • если три грани, две из которых противоположны друг другу, имеют один цвет, а три других - другого цвета, куб имеет 4 изометрии.
  • если две противоположные грани имеют один и тот же цвет, а две другие противоположные грани тоже, а последние две имеют разные цвета, куб имеет 4 изометрии, как лист чистой бумаги с формой с зеркальной симметрией.
• C _s , [], (*):
  • если две смежные грани имеют цвета, отличные друг от друга, а четыре других имеют третий цвет, куб имеет 2 изометрии.
  • если две противоположные грани имеют один и тот же цвет, а все остальные грани имеют разные цвета, куб имеет 2 изометрии, как асимметричный лист чистой бумаги.
• C _{3 v} , [3], (* 33): если три грани, ни одна из которых не противоположна друг другу, имеют один цвет, а три другие - другого цвета, куб имеет 6 изометрий.

Для некоторых более крупных подгрупп куб с этой группой в качестве группы симметрии невозможно с простой окраской целых граней. На лицах нужно нарисовать какой-то узор.

Примеры:

• D _{2 d} , [2 ⁺ , 4], (2 * 2): если на одной грани есть отрезок прямой, разделяющий грань на два равных прямоугольника, а на противоположной - такой же в перпендикулярном направлении, куб имеет 8 изометрий; существует плоскость симметрии и 2-кратная ось симметрии вращения с осью под углом 45 ° к этой плоскости, и, как следствие, существует также другая плоскость симметрии, перпендикулярная первой, и другая ось 2-кратной симметрии вращения перпендикулярно первому.
• T _h , [3 ⁺ , 4], (3 * 2): если каждая грань имеет отрезок линии, разделяющий грань на два равных прямоугольника, так что отрезки смежных граней не пересекаются на краю, куб имеет 24 изометрии: четные перестановки диагоналей тела и то же самое в сочетании с инверсией ( x отображается в - x ).
• T _d , [3,3], (* 332): если куб состоит из восьми меньших кубов, четырех белых и четырех черных, соединенных поочередно во всех трех стандартных направлениях, куб снова имеет 24 изометрии: на этот раз четные перестановки диагоналей тела и инверсии других собственных вращений.
• T , [3,3] ⁺ , (332): если каждая грань имеет одинаковый узор с 2-кратной симметрией вращения, скажем, буквой S, так что на всех краях вершина одной S пересекает сторону другой S, куб имеет 12 изометрий: четные перестановки диагоналей тела.

Полная симметрия куба, O _h , [4,3], (* 432), сохраняется тогда и только тогда, когда все грани имеют одинаковый узор, такой, что сохраняется полная симметрия квадрата , а для квадрата симметрия группа, Dih 4 , [4], порядка 8.

Полная симметрия куба относительно собственных вращений, O , [4,3] ⁺ , (432), сохраняется тогда и только тогда, когда все грани имеют одинаковый образец с 4-кратной симметрией вращения , C ₄ , [4] ⁺ .

Октаэдрическая симметрия поверхности Больца [ править ]

В теории римановой поверхности поверхность Больца , иногда называемая кривой Больца, получается как разветвленное двойное покрытие сферы Римана с местом ветвления в множестве вершин правильного вписанного октаэдра. Его группа автоморфизмов включает гиперэллиптическую инволюцию, переворачивающую два листа покрытия. Фактор по подгруппе порядка 2, порожденной гиперэллиптической инволюцией, дает в точности группу симметрий октаэдра. Среди многих замечательных свойств поверхности Больца - тот факт, что она максимизирует систолу среди всех гиперболических поверхностей рода 2.

Твердые тела с октаэдрической киральной симметрией [ править ]

Твердые тела с полной октаэдрической симметрией [ править ]

См. Также [ править ]

• Тетраэдрическая симметрия
• Икосаэдрическая симметрия
• Бинарная октаэдрическая группа
• Гипероктаэдрическая группа
• Учебные материалы, связанные с октаэдрической группой в Викиверситете

Ссылки [ править ]

• Питер Р. Кромвель, Многогранники (1997), стр. 295
• Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, ISBN  978-1-56881-220-5
• Калейдоскопы: Избранные сочинения HSM Coxeter , отредактированные Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1] 
• Н. В. Джонсон : геометрии и преобразования , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , 11.5 Сферические группы Кокстера 

Внешние ссылки [ править ]

• Вайсштейн, Эрик В. «Октаэдрическая группа» . MathWorld .
• Groupprops: прямое произведение S4 и Z2