Лестница парадокс (или амбар-полюсный парадокс ) является мысленным экспериментом в специальной теории относительности . Он включает в себя лестницу, параллельную земле, движущуюся горизонтально с релятивистской скоростью (близкой к скорости света) и, следовательно, испытывающую сокращение длины Лоренца . Представьте себе, что лестница проходит через открытые переднюю и заднюю двери гаража или сарая, длина которой меньше его остальной длины., поэтому, если бы лестница не двигалась, она не могла бы поместиться внутрь. Для неподвижного наблюдателя из-за сжатия движущаяся лестница может полностью помещаться внутри здания, когда она проходит. С другой стороны, с точки зрения наблюдателя, движущегося по лестнице, лестница не будет сокращена, и это здание будет сокращено Лоренцом до еще меньшей длины. Следовательно, лестница не сможет поместиться внутри здания, когда она будет проходить. Это создает очевидное несоответствие между реальностями обоих наблюдателей.
Этот кажущийся парадокс является результатом ошибочного предположения об абсолютной одновременности. Считается, что лестница вписывается в гараж, если можно сделать так, чтобы оба ее конца одновременно находились внутри гаража. Парадокс разрешается, если принять во внимание, что в теории относительности одновременность относится к каждому наблюдателю, что дает ответ на вопрос, подходит ли лестница внутри гаража, также относительно каждого из них.
Парадокс [ править ]
Самый простой вариант проблемы связан с гаражом с открытыми передней и задней дверью и лестницей, которая в состоянии покоя относительно гаража слишком длинна, чтобы поместиться внутрь. Теперь мы перемещаем лестницу с большой горизонтальной скоростью через стационарный гараж. Из-за своей высокой скорости лестница подвергается релятивистскому эффекту сокращения длины и становится значительно короче. В результате, проходя через гараж, лестница какое-то время полностью удерживается внутри него. При желании мы могли бы одновременно закрыть обе двери на короткое время, чтобы продемонстрировать, что лестница подходит.
Пока это согласуется. Кажущийся парадокс возникает, когда мы рассматриваем симметрию ситуации. Поскольку наблюдатель, движущийся по лестнице, движется с постоянной скоростью в инерциальной системе отсчета гаража, этот наблюдатель также находится в инерциальной системе отсчета, где, согласно принципу относительности , действуют те же законы физики. С этой точки зрения лестница теперь неподвижна, а гараж движется с большой скоростью. Следовательно, это гараж, который сокращен по длине, и теперь мы делаем вывод, что он слишком мал, чтобы когда-либо полностью вмещать лестницу, когда она проходила: лестница не подходит, и мы не можем закрыть обе двери с обеих сторон лестницы. не задев его. Это кажущееся противоречие и есть парадокс.
Разрешение [ править ]
Решение очевидного парадокса заключается в относительности одновременности.: то, что один наблюдатель (например, с гаражом) считает двумя одновременными событиями, на самом деле может не быть одновременным для другого наблюдателя (например, с лестницей). Когда мы говорим, что лестница «вписывается» в гараж, мы имеем в виду именно то, что в определенное время как задняя часть лестницы, так и позиция передней части лестницы находились внутри гаража; Другими словами, передняя и задняя часть лестницы находились внутри гаража одновременно. Поскольку одновременность относительна, два наблюдателя расходятся во мнениях относительно того, подходит ли лестница. Для наблюдателя с гаражом задний конец лестницы находился в гараже одновременно с передним концом лестницы, и поэтому лестница подходила; но для наблюдателя с лестницей эти два события не были одновременными, и лестница не подходила.
Ясный способ увидеть это - рассмотреть двери, которые в раме гаража закрываются на то короткое время, когда лестница полностью находится внутри. Теперь посмотрим на эти события в рамках лестницы. Первое событие - это передняя часть лестницы, ведущая к выходу из гаража. Дверь закрывается, а затем снова открывается, пропуская переднюю часть лестницы. Позже задняя часть лестницы проходит через входную дверь, которая закрывается, а затем открывается. Мы видим, что, поскольку одновременность относительна, две двери не нужно было закрывать одновременно, и лестнице не нужно было помещаться внутри гаража.
Ситуация может быть дополнительно проиллюстрирована диаграммой Минковского ниже. Схема находится в остальной раме гаража. Вертикальная голубая полоса показывает гараж в пространстве-времени, а светло-красная полоса показывает лестницу в пространстве-времени. Оси x и t - это оси пространства гаража и времени соответственно, а x ′ и t ′ - оси пространства лестницы и времени соответственно.
В кадре гаража лестница в любой конкретный момент времени представлена горизонтальным набором точек, параллельных оси x, в красной полосе. Одним из примеров является полужирный синий сегмент линии, который находится внутри синей полосы, представляющей гараж, и представляет собой лестницу в то время, когда она полностью находится внутри гаража. Однако в рамках лестницы наборы одновременных событий лежат на линиях, параллельных оси x '; поэтому лестница в любой конкретный момент времени представлена поперечным сечением такой линии с красной полосой. Одним из таких примеров является жирный красный отрезок линии. Мы видим, что такие отрезки никогда не лежат полностью внутри синей полосы; то есть лестница никогда не лежит полностью внутри гаража.

Закрытие лестницы в гараже [ править ]
В более сложной версии парадокса мы можем физически заблокировать лестницу, когда она полностью окажется внутри гаража. Это можно сделать, например, если не открывать выходную дверь снова после того, как мы ее закроем. В рамках гаража мы предполагаем, что выходная дверь неподвижна, и поэтому, когда лестница ударяется о нее, мы говорим, что она мгновенно останавливается. [1] [2] К этому времени входная дверь тоже закрылась, и лестница застряла внутри гаража. Поскольку его относительная скорость теперь равна нулю, длина не сокращена, и теперь он длиннее, чем гараж; он должен будет согнуться, сломаться или взорваться.
Опять же, загадка возникает из-за рассмотрения ситуации с рамы лестницы. В приведенном выше анализе лестница в собственном каркасе всегда была длиннее гаража. Так как же нам удалось закрыть двери и запереть его внутри?
Здесь стоит отметить общую особенность теории относительности: мы пришли к выводу, рассматривая каркас гаража, что мы действительно запираем лестницу внутри гаража. Следовательно, это должно быть верно для любого кадра - лестница не может защелкнуться в одном кадре, но не в другом. Таким образом, по раме лестницы мы знаем, что должно быть какое-то объяснение того, как лестница оказалась в ловушке; мы должны просто найти объяснение.
Объяснение заключается в том, что хотя все части лестницы одновременно замедляются до нуля в раме гаража, поскольку одновременность относительна, соответствующие замедления в раме лестницы не одновременны. Вместо этого каждая часть лестницы последовательно замедляется [1] [3] спереди назад, пока, наконец, не замедлится задняя часть лестницы, и к этому времени она уже будет в гараже.
Поскольку сокращение длины и замедление времени контролируются преобразованиями Лоренца , лестничный парадокс можно рассматривать как физический коррелят парадокса близнецов., в котором один из близнецов покидает Землю, какое-то время путешествует со скоростью и возвращается на Землю немного моложе, чем привязанный к Земле близнец. Как и в случае с лестницей, застрявшей внутри сарая, если ни одна из систем отсчета не является привилегированной - каждый движется только относительно другого - как может быть, что это путешествующий близнец, а не неподвижный, который младше (точно так же, как он лестница, а не сарай, который короче)? В обоих случаях именно ускорение-замедление различает явления: именно двойник, а не земля (или лестница, а не сарай), подвергается силе замедления, возвращаясь во временное (или физическое, в случае лестница-сарай) инерционная рама.

Парадокс лестницы и передача силы [ править ]
Что делать, если задняя дверь (дверь, из которой выходит лестница) закрыта навсегда и не открывается? Предположим, что дверь настолько прочная, что лестница не пробьет ее при столкновении, поэтому она должна остановиться. Затем, как в сценарии, описанном выше, в системе отсчета гаража наступает момент, когда лестница полностью находится внутри гаража (т. Е. Задняя часть лестницы находится внутри входной двери), прежде чем она сталкивается с дверью. задняя дверь и останавливается. Однако, исходя из системы координат лестницы, лестница слишком велика, чтобы поместиться в гараже, поэтому к тому времени, когда она сталкивается с задней дверью и останавливается, задняя часть лестницы все еще не достигает входной двери. Это кажется парадоксом. Вопрос в том, пересекает ли задняя часть лестницы входную дверь или нет?
Сложность возникает в основном из-за предположения, что лестница является жесткой (т. Е. Сохраняет ту же форму). В повседневной жизни лестницы кажутся жесткими. Но для того, чтобы быть полностью жестким, необходимо, чтобы он мог передавать силу с бесконечной скоростью (то есть, когда вы толкаете один конец, другой конец должен немедленно реагировать, иначе лестница деформируется). Это противоречит специальной теории относительности, которая утверждает, что информация может перемещаться не быстрее скорости света (что слишком быстро для нас, чтобы заметить в реальной жизни, но имеет значение в лестничном сценарии). Таким образом, объекты не могут быть абсолютно жесткими согласно специальной теории относительности.
В этом случае к тому времени, когда передняя часть лестницы сталкивается с задней дверью, задняя часть лестницы еще не знает об этом, поэтому продолжает движение вперед (и лестница «сжимается»). Как в раме гаража, так и в инерциальной раме лестницы задний конец продолжает двигаться во время столкновения, по крайней мере, до точки, где задняя часть лестницы входит в световой конус столкновения (т. Е. точка, в которой сила, движущаяся назад со скоростью света от точки столкновения, достигнет ее). На этом этапе лестница фактически короче, чем исходная сокращенная длина, поэтому задняя часть находится внутри гаража. Расчеты в обеих системах отсчета покажут, что это так.
Что происходит после того, как сила достигает задней части лестницы («зеленая» зона на диаграмме), не уточняется. В зависимости от физики лестница могла сломаться; или, если бы он был достаточно эластичным, он мог бы изгибаться и снова расширяться до своей первоначальной длины. На достаточно высоких скоростях любой реалистичный материал взорвался бы в плазму.
Человек падает на решетку [ править ]
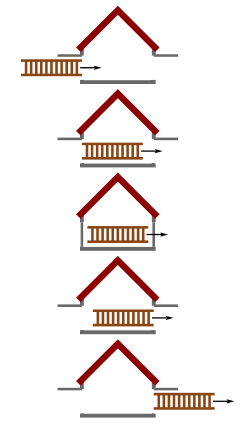
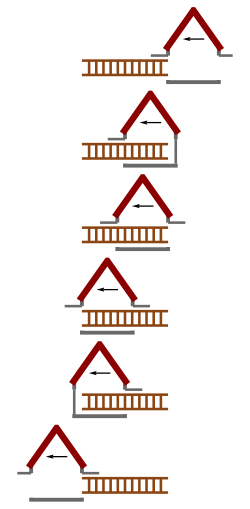
Эта ранняя версия парадокса была первоначально предложена и разрешена Вольфгангом Риндлером [1] и предполагала, что быстро идущий человек, представленный жезлом, упал в решетку. [4] Предполагается, что стержень полностью находится над решеткой в системе отсчета решетки до того, как одновременно начнется ускорение вниз, приложенное к каждой точке стержня.
С точки зрения решетки стержень сокращается по длине и входит в решетку. Однако, с точки зрения стержня, решетка испытывает сокращение длины, из-за чего кажется, что стержень слишком длинный, чтобы упасть.
Ускорение стержня вниз, которое является одновременным в системе отсчета решетки, не является одновременным в системе отсчета стержня. В системе отсчета стержня передняя часть стержня сначала ускоряется вниз (показано в ячейке 3 на чертеже), и с течением времени все больше и больше стержня подвергается ускорению вниз, пока, наконец, не задняя часть стержня. стержень ускоряется вниз. Это приводит к изгибу стержня в системе отсчета стержня. Так как этот изгиб происходит в системе покоя стержня, это истинное физическое искажение стержня, который будет вызывать стрессы происходят в стержне.
Чтобы это нежесткое поведение стержня стало очевидным, и сам стержень, и решетка должны иметь такой масштаб, чтобы можно было измерить время перемещения.
Парадокс бара и кольца [ править ]
Проблема, очень похожая, но более простая, чем парадокс стержня и решетки, включающая только инерциальные системы отсчета, - это парадокс «стержня и кольца» (Ferraro 2007). Парадокс стержня и решетки сложен: он включает в себя неинерциальные системы отсчета, поскольку в один момент человек идет горизонтально, а через мгновение он падает вниз; и это связано с физической деформацией человека (или сегментированного стержня), поскольку стержень изогнут в одной системе отсчета и прямой в другой. Эти аспекты проблемы вносят осложнения, связанные с жесткостью стержня, которая имеет тенденцию затемнять реальную природу «парадокса». Парадокс «стержня и кольца» лишен этих сложностей: стержень, длина которого немного превышает диаметр кольца, движется вверх и вправо, а его длинная ось горизонтальна,в то время как кольцо неподвижно, и плоскость кольца также горизонтальна. Если движение штанги таково, что центр штанги в какой-то момент времени совпадает с центром кольца, то штанга будет сжиматься по Лоренцеву из-за поступательного компонента ее движения, и она пройдет через звенеть. Парадокс возникает, когда проблема рассматривается в остальной части бара. Кольцо теперь движется вниз и влево и будет сжато по Лоренцу по своей горизонтальной длине, в то время как штанга не будет сокращена вообще. Как штанга проходит через кольцо?и он пройдет через кольцо. Парадокс возникает, когда проблема рассматривается в остальной части бара. Кольцо теперь движется вниз и влево и будет сжато по Лоренцу по своей горизонтальной длине, в то время как штанга не будет сокращена вообще. Как штанга проходит через кольцо?и он пройдет через кольцо. Парадокс возникает, когда проблема рассматривается в остальной части бара. Кольцо теперь движется вниз и влево и будет сжато по Лоренцу по своей горизонтальной длине, в то время как штанга не будет сокращена вообще. Как штанга проходит через кольцо?
Разрешение парадокса снова заключается в относительности одновременности (Ferraro 2007). Длина физического объекта определяется как расстояние между двумя одновременными событиями, происходящими на каждом конце тела, и, поскольку одновременность относительна, эта длина относительна. Эта изменчивость длины и есть сокращение Лоренца. Точно так же физический угол определяется как угол, образованный тремя одновременнымисобытий, и этот угол тоже будет относительной величиной. В приведенном выше парадокс, хотя стержень и плоскость кольца параллельны в системе покоя кольца, они не параллельны в системе покоя стержня. Несжатый стержень проходит через лоренц-сжатое кольцо, поскольку плоскость кольца поворачивается относительно стержня на величину, достаточную для того, чтобы стержень прошел сквозь него.
С математической точки зрения преобразование Лоренца можно разделить на произведение пространственного вращения и «собственное» преобразование Лоренца, которое не включает пространственного вращения. Математическое разрешение парадокса стержня и кольца основано на том факте, что произведение двух собственных преобразований Лоренца (горизонтального и вертикального) может дать преобразование Лоренца, которое не является правильным (диагональным), а скорее включает компонент пространственного вращения.
См. Также [ править ]
- Парадокс космического корабля Белла
- Парадокс Эренфеста
- Физический парадокс
- Относительность одновременности
- Парадокс Supplee
- Парадокс близнецов
Примечания [ править ]
- ^ a b c Риндлер, Вольфганг (1961). «Парадокс сокращения длины». Американский журнал физики . 29 (6): 365–366. Bibcode : 1961AmJPh..29..365R . DOI : 10.1119 / 1.1937789 .
- ^ Риндлер описывает стержень, который испытывает одновременное ускорение
- ^ Риндлер описывает стержень, подвергающийся последовательному ускорению.
- ^ Эдвин Ф. Тейлор; Джон Арчибальд Уиллер (1992). Физика пространства-времени: Введение в специальную теорию относительности . Нью-Йорк: WH Freeman. С. 116 . ISBN 0-7167-2327-1.
Ссылки [ править ]
- Уэллс, Уиллард Х. (1961). «Парадокс длины в теории относительности». Американский журнал физики . 29 (12): 858. Bibcode : 1961AmJPh..29..858W . DOI : 10.1119 / 1.1937641 .
- Шоу, Р. (1962). «Парадокс сокращения длины». Американский журнал физики . 30 (1): 72. Bibcode : 1962AmJPh..30 ... 72S . DOI : 10.1119 / 1.1941907 .
- Мартинс, Роберто Де А. (1978). «Парадокс длины в теории относительности». Американский журнал физики . 46 (6): 667–670. Bibcode : 1978AmJPh..46..667M . DOI : 10.1119 / 1.11227 .
- Састри, ГП (1987). «Неужели сокращение длины действительно парадоксально?». Американский журнал физики . 55 (10): 943–946. Bibcode : 1987AmJPh..55..943S . DOI : 10.1119 / 1.14911 .
- Грён, Ойвинд; Йоханнесен, Стейнар (1993). «Компьютерное моделирование парадокса сокращения длины Риндлера». Европейский журнал физики . 14 (3): 97–100. Bibcode : 1993EJPh ... 14 ... 97g . DOI : 10.1088 / 0143-0807 / 14/3/001 .
- ван Линтель, Харальд; Грубер, Кристиан (2005). «Переосмысление парадокса стержня и отверстия» . Европейский журнал физики . 26 (1): 19–23. Bibcode : 2005EJPh ... 26 ... 19V . DOI : 10.1088 / 0143-0807 / 26/1/003 . S2CID 121888743 .
- Айер, Чандру; Прабху, GM (2008). «Реверс во временном порядке интерактивных событий: столкновение наклонных стержней». Европейский журнал физики . 27 (4): 819–824. arXiv : 0809.1721 . Bibcode : 2006EJPh ... 27..819I . DOI : 10.1088 / 0143-0807 / 27/4/013 . S2CID 117711286 .
- Пирс, Эван (2007). «Парадокс замка и ключа и пределы жесткости в специальной теории относительности». Американский журнал физики . 75 (7): 610–614. Bibcode : 2007AmJPh..75..610P . DOI : 10.1119 / 1.2711827 .
- Айер, Чандру; Прабху, GM (2008). «Разные наблюдения по посадке стержня в паз». Американский журнал физики . 74 (11): 998–1001. arXiv : 0809.1740 . Bibcode : 2006AmJPh..74..998I . DOI : 10,1119 / 1,2346686 . S2CID 55801261 .
- МакГлинн, Энда; ван Кампен, Пол (2008). «Заметка о связи электрического тока, магнитных полей, зарядов и полюса в парадоксе сарая в специальной теории относительности». Европейский журнал физики . 29 (6): N63 – N67. Bibcode : 2008EJPh ... 29 ... 63M . DOI : 10.1088 / 0143-0807 / 29/6 / N03 .
Дальнейшее чтение [ править ]
- Эдвин Ф. Тейлор и Джон Арчибальд Уиллер, Физика пространства-времени (2-е изд) (Фриман, Нью-Йорк, 1992)
- - обсуждает различные очевидные парадоксы СТО и их решения.
- Риндлер, Вольфганг (2001). Относительность: специальная, общая и космологическая . Издательство Оксфордского университета. ISBN 0-19-850836-0.
- Ферраро, Рафаэль (2007). Пространство-время Эйнштейна: введение в специальную и общую теорию относительности . Springer . ISBN 978-0-387-69946-2.
Внешние ссылки [ править ]
| Викискладе есть медиафайлы по теме парадокса лестницы . |
- Анимация специальной теории относительности от Джона де Пиллиса. Этот интерактивный анимированный парадокс поезда и туннеля является аналогом парадокса полюса (поезда) и сарая (туннеля).