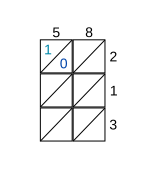Решеточное умножение , также известное как итальянский метод , китайский метод , китайская решетка , умножение гелозии , [1] умножение решет , шабах , диагональные или венецианские квадраты , - это метод умножения, который использует решетку для умножения двух многозначных чисел. Математически он идентичен более часто используемому алгоритму длинного умножения , но разбивает процесс на более мелкие этапы, которые некоторым практикам легче использовать. [2]
Этот метод возник еще в средние века и веками использовался во многих различных культурах. Его по-прежнему преподают в определенных учебных программах. [3] [4]
Метод [ править ]
Составлена сетка, и каждая ячейка разбита по диагонали. Два множителя вычисляемого продукта записываются вдоль верхней и правой стороны решетки, соответственно, с одной цифрой в столбце сверху для первого множимого (число, записываемым слева направо) и одной цифрой в строке вниз. правая часть второго множимого (число, записанное сверху вниз). Затем каждая ячейка решетки заполняется произведением ее цифры столбца и строки.
В качестве примера рассмотрим умножение 58 на 213. После записи множителей по бокам рассмотрите каждую ячейку, начиная с верхней левой ячейки. В этом случае цифра столбца равна 5, а цифра строки - 2. Запишите их произведение, 10, в ячейку, указав цифру 1 над диагональю и цифру 0 под диагональю (см. Рисунок для шага 1).
Если в простом продукте отсутствует цифра в разряде десятков, просто замените разряды десятков цифрой 0. [2]
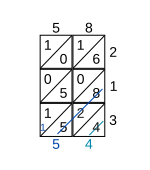
После того, как все ячейки будут заполнены таким образом, цифры на каждой диагонали суммируются, работая от нижней правой диагонали к верхней левой. Каждая диагональная сумма записывается там, где заканчивается диагональ. Если сумма содержит более одной цифры, значение разряда десятков переносится на следующую диагональ (см. Шаг 2).
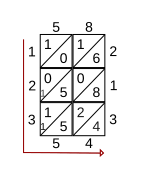
Цифры заполняются слева и снизу сетки, и ответ - числа, считанные снизу (слева) и поперек (снизу). В показанном примере результат умножения 58 на 213 составляет 12354.
Умножение десятичных дробей [ править ]
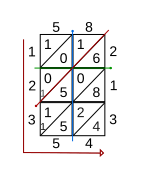
Метод решетки также может использоваться для умножения десятичных дробей . Например, умножение 5,8 на 2,13 происходит так же, как умножение 58 на 213, как описано в предыдущем разделе. Чтобы найти положение десятичной точки в окончательном ответе, можно провести вертикальную линию от десятичной точки в 5.8 и горизонтальную линию от десятичной точки в 2.13. (См. Рисунок для шага 4.) Диагональ сетки, проходящая через пересечение этих двух линий, затем определяет положение десятичной точки в результате. [2] В показанном примере результат умножения 5,8 и 2,13 равен 12,354.
История [ править ]
Решетчатое умножение исторически использовалось во многих различных культурах. Неизвестно, где он впервые возник и развивался ли он независимо более чем в одном регионе мира. [5] Самое раннее зарегистрированное использование решеточного умножения: [6]
- в арабской математике был написан Ибн аль-Банна аль-Марракуши в его « Талхих амал аль-Хисаб» в Магрибе в конце 13 века.
- в европейской математике был написан неизвестным автором латинского трактата в Англии Tractatus de minutisphilusphicis et vulgaribus , c. 1300
- в китайской математике был У Цзин в его Jiuzhang suanfa bilei daquan , завершенном в 1450 году.
Математик и педагог Дэвид Юджин Смит утверждал, что решеточное умножение пришло в Италию с Ближнего Востока. [7] Это подкрепляется указанием на то , что арабский термин для метода, шабах , имеет то же значение, что и итальянский термин для метода, гелосия , а именно металлическая решетка или решетка (решетка) для окна.
Иногда ошибочно утверждается, что решеточное умножение было описано Мухаммадом ибн Муса аль-Хваризми (Багдад, ок. 825) или Фибоначчи в его Liber Abaci (Италия, 1202, 1228). [8] На самом деле, однако, ни один из этих двух авторов не нашел использования решеточного умножения. В главе 3 своего Liber Abaci , Фибоначчи делают описать связанный метод умножения на то , что он назвал Quadrilatero в Форме scacherii(«Прямоугольник в виде шахматной доски»). В этой технике квадратные ячейки не разделяются по диагонали; в каждую ячейку записывается только цифра младшего разряда, в то время как любую цифру более высокого порядка необходимо запомнить или записать в другом месте, а затем «перенести» для добавления в следующую ячейку. Это контрастирует с решетчатым умножением, отличительной особенностью которого является то, что каждая ячейка прямоугольника имеет собственное правильное место для цифры переноса; это также означает, что ячейки могут быть заполнены в любом желаемом порядке. Свец [9] сравнивает и противопоставляет умножение с помощью gelosia (решетки), scacherii (шахматной доски) и других табличных методов.
Другие известные исторические применения решеточного умножения включают: [6]
- «Мифтах аль-Хисаб » Джамшида аль-Каши (Самарканд, 1427 г.), в котором используются шестидесятеричные числа (основание 60), а сетка повернута на 45 градусов в сторону «ромба».
- Arte dell'Abbaco , анонимный текст , опубликованный в венецианском диалекте в 1478 году , часто называют Treviso арифметике , потому что она была напечатана в Тревизо, просто вдали от Венеции, Италия
- Лука Пачоли «s Summa де Арифметика (Венеция, 1494)
- индийский астроном комментарий Ganesa на Бхаскар II «s Lilavati (16 век).
Производные [ править ]
Выводы этого метода также появились в работах 16- го века « Умдет-уль-Хисаб » османско-боснийского эрудита Матракчи Насуха . [10] Треугольная версия метода умножения Матракчи Насуха показана в примере, показывающем 155 x 525 справа, и объяснена в примере, показывающем 236 x 175 на левом рисунке. [11]
Тот же принцип, описанный Матракчи Насухом, лег в основу более позднего развития счетных стержней, известных как кости Напьера (Шотландия, 1617 г.) и правителей Генайя-Лукаса (Франция, конец 1800-х гг.).
Ссылки [ править ]
- ^ Уильямс, Майкл Р. (1997). История вычислительной техники (2-е изд.). Лос-Аламитос, Калифорния: Пресса компьютерного общества IEEE. ISBN 0-8186-7739-2. OCLC 35723637 .
- ^ a b c Томас, Вики (2005). «Решеточное умножение» . Изучите NC . Педагогическая школа UNC . Проверено 4 июля 2014 года .
- ^ Боаг, Элизабет, «Решеточное умножение», Бюллетень BSHM: Журнал Британского общества истории математики 22: 3 (ноябрь 2007 г.), стр. 182.
- ^ Нуджент, Патриция М., «Умножение решеток в классе Preservice», Преподавание математики в средней школе 13: 2 (сентябрь 2007 г.), стр. 110–113.
- ^ Жан-Люк Шабер, изд., История алгоритмов: от гальки до микрочипа (Берлин: Springer, 1999), стр. 21.
- ^ a b Жан-Люк Шабер, редактор, История алгоритмов: от камешка до микрочипа (Берлин: Springer, 1999), стр. 21-26.
- ^ Смит, Дэвид Юджин, История математики , Vol. 2, «Специальные разделы элементарной математики» (Нью-Йорк: Довер, 1968).
- ↑ Оригинальная версия Liber Abaci 1202 годаутеряна. Версия 1228 года была позже опубликована на оригинальной латыни в Boncompagni, Baldassarre, Scritti di Leonardo Pisano , vol. 1 (Рим: Типография делле научная математика и физика, 1857 г.); английский перевод того же был опубликован Сиглером, Лоуренсом Э., Liber Abaci Фибоначчи: перевод на современный английский книги расчетов Леонардо Пизано (Нью-Йорк: Springer Verlag, 2002).
- ^ Swetz, Frank J., Капитализм и арифметика: Новая математика 15 - го века, в том числе полный текст Тревизо Арифметика 1478, переведенный Дэвид Юджин Смит (La Salle, IL: Open Court, 1987)., Стр 205 -209.
- ^ Корлу, МС, Burlbaw, Л.М., Capraro, Р.М., Корлу, М., & Хан, С. (2010). «Школа Османского дворца Эндерун и Человек с множеством талантов, Матракчи Насух». Журнал Корейского общества математического образования , серия D: Исследования в области математического образования. 14 (1), стр. 19-31.
- ^ https://tamu.academia.edu/SencerCorlu/Papers/471488/The_Ottoman_Palace_School_Enderun_and_the_Man_with_Multiple_Talents_Matrakci_Nasuh