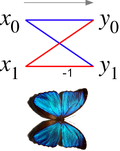Математические диаграммы , такие как диаграммы и графики , в основном предназначены для передачи математических взаимосвязей, например, сравнения во времени. [1]
Определенные типы математических диаграмм [ править ]
Диаграмма Аргана [ править ]
Комплексное число может быть визуально представлено в виде пары чисел , образующих вектор на диаграмме , называемом Арганд диаграммой , комплексная плоскость иногда называют плоскость Арганды , поскольку он используется в диаграммах Арган . Они названы в честь Жана-Робера Аргана (1768–1822), хотя впервые были описаны норвежско-датским землемером и математиком Каспаром Весселем (1745–1818). [2] Арганда диаграмма часто используется для построения позиций полюсов и нулей в виде функции в комплексной плоскости.
Концепция комплексной плоскости позволяет геометрическую интерпретацию комплексных чисел. При добавлении они складывают похожие векторы . Умножение двух комплексных чисел могут быть выражены наиболее легко в полярных координатах - величина , или модуль продукта является произведением двух абсолютных величин , или модулей, а угол или аргумент продукта является суммой двух углов, или аргументы. В частности, умножение на комплексное число по модулю 1 действует как поворот.
Диаграмма бабочки [ править ]
В контексте алгоритмов быстрого преобразования Фурье « бабочка» - это часть вычислений, которая объединяет результаты меньших дискретных преобразований Фурье (ДПФ) в большее ДПФ или наоборот (разбиение большего ДПФ на частичные преобразования). Название «бабочка» происходит от формы диаграммы потока данных в случае radix-2, как описано ниже. Такую же структуру можно найти в алгоритме Витерби , который используется для поиска наиболее вероятной последовательности скрытых состояний.
Диаграмма « бабочка» показывает диаграмму потока данных, соединяющую входы x (слева) с выходами y, которые зависят от них (справа) для шага «бабочка» алгоритма БПФ Кули – Тьюки с основанием 2 . Эта диаграмма похожа на бабочку, как на морфо-бабочке, показанной для сравнения), отсюда и название.
Коммутативная диаграмма [ править ]
В математике, и особенно в теории категорий , коммутативная диаграмма - это диаграмма объектов , также известных как вершины, и морфизмов , также известных как стрелки или ребра, так что при выборе двух объектов любой направленный путь через диаграмму приводит к одному и тому же результату. по составу.
Коммутативные диаграммы играют роль в теории категорий, которую уравнения играют в алгебре.
Диаграммы Хассе [ править ]
Диаграмма Хассы является простой картиной конечного частично упорядоченного множества , формируя рисунок частичного порядка в переходном сокращении . Конкретно, каждый элемент набора представляет собой вершину на странице и рисует линейный сегмент или кривую, идущую вверх от x к y, именно тогда, когда x < y и нет z, такого что x < z < y . В этом случае мы говорим, что y покрываетx или y является непосредственным преемником x. На диаграмме Хассе требуется, чтобы кривые были нарисованы так, чтобы каждая встречалась ровно с двумя вершинами: двумя своими конечными точками. Любая такая диаграмма (при условии, что вершины помечены) однозначно определяет частичный порядок, и любой частичный порядок имеет уникальную транзитивную редукцию, но есть много возможных размещений элементов на плоскости, что приводит к различным диаграммам Хассе для данного порядка, которые могут имеют очень разный внешний вид.
Диаграммы узлов [ править ]
В теории узлов полезный способ визуализировать узлы и управлять ими - это спроецировать узел на плоскость - представьте себе узел, отбрасывающий тень на стену. Небольшое отклонение в выборе проекции гарантирует, что она будет взаимно однозначной, за исключением двойных точек, называемых пересечениями , где «тень» узла пересекает себя один раз в поперечном направлении [3]
На каждом перекрестке мы должны указывать, какой участок «сверху», а какой «под», чтобы иметь возможность воссоздать исходный узел. Часто это делается путем создания разрыва пряди, идущей снизу. Если, следуя схеме, узел попеременно пересекает себя «сверху» и «снизу», то диаграмма представляет собой особенно хорошо изученный класс узлов, чередующихся узлов .
Диаграмма Венна [ править ]
Диаграмма Венна является представлением математических множеств: математическая схема , представляющая наборы в виде кружков, с их отношениями друг к другу выражается через их перекрывающиеся позиции, так что все возможные соотношения между множествами показаны. [4]
Диаграмма Венна построена из набора простых замкнутых кривых, нарисованных на плоскости. Принцип этих диаграмм состоит в том, что классы представлены регионами в таком отношении друг к другу, что все возможные логические отношения этих классов могут быть указаны на одной диаграмме. То есть диаграмма изначально оставляет место для любого возможного отношения классов, а фактическое или данное отношение затем может быть указано, указав, что некоторая конкретная область имеет значение NULL или не является нулевым. [5]
Диаграмма Вороного [ править ]
Диаграмма Вороного представляет собой особый вид разложения метрического пространства определяется расстояниями до заданного дискретного множества объектов в пространстве, например, с помощью дискретного множества точек. Эта диаграмма названа в честь Георгия Вороного , также называемая тесселяцией Вороного, разложением Вороного или тесселяцией Дирихле в честь Питера Густава Лежена Дирихле .
В простейшем случае нам дан набор точек S на плоскости, которые являются узлами Вороного. Каждый сайт s имеет ячейку Вороного V (s), состоящую из всех точек, более близких к s, чем к любому другому сайту. Сегменты диаграммы Вороного - это все точки на плоскости, которые равноудалены двум участкам. Узлы Вороного - это точки, равно удаленные от трех (или более) участков.
Диаграммы групп обоев [ править ]
Обои группа или плоская группа симметрии или плоскость кристаллографической группа представляет собой математическая классификация двумерный повторяющегося рисунка, на основе симметрий в шаблоне. Такие узоры часто встречаются в архитектуре и декоративном искусстве. Есть 17 возможных отдельных групп .
Группы обоев - это двумерные группы симметрии , промежуточные по сложности между более простыми фризовыми группами и трехмерными кристаллографическими группами , также называемыми пространственными группами . Группы обоев классифицируют узоры по их симметрии. Незначительные различия могут помещать похожие узоры в разные группы, в то время как узоры, которые сильно различаются по стилю, цвету, масштабу или ориентации, могут принадлежать к одной группе.
Диаграмма Юнга [ править ]
Диаграмма Юнга или Юнга , называемая также Феррерс диаграммой , является конечным набором коробка, или клеток, расположенным в левых выравнивании строк, причем строка размеров слабо снижается (каждая строка имеет такую же или меньшую длину , чем его предшественник).
Перечисление количества ящиков в каждой строке дает разделение положительного целого числа n - общего количества ящиков на диаграмме. Диаграмма Юнга имеет форму и несет ту же информацию, что и этот раздел. Указание количества ящиков в каждом столбце дает другой раздел, сопряженный или транспонированный раздел ; диаграмму Юнга этой формы можно получить, отразив исходную диаграмму вдоль ее главной диагонали.
Таблицы Юнга были введены Альфредом Янгом , математиком из Кембриджского университета , в 1900 году. Затем они были применены к изучению симметрических групп Георгом Фробениусом в 1903 году. Их теория получила дальнейшее развитие у многих математиков.
Другие математические диаграммы [ править ]
- Диаграмма Кремоны
- Диаграмма де Финетти
- Диаграмма Дынкина
- Элементарная схема
- Диаграмма Эйлера
- Звездчатая диаграмма
- Спираль Улама
- Диаграмма Ван Кампена
- Диаграмма Тейлора
См. Также [ править ]
- Теория категорий
- Логическая диаграмма
- Математический жаргон
- Математическая модель
- Математика как язык
- Математическая визуализация
- Статистическая модель
Ссылки [ править ]
- ^ Работа с диаграммами в LearningSpace.
- ^ Мемуар Вессель был представлен датской академии в 1797 году; Статья Аргана была опубликована в 1806 году
( Whittaker, Edmund Taylor; Watson, GN (1927). Курс современного анализа : введение в общую теорию бесконечных процессов и аналитических функций с учетом основных трансцендентных функций . Кембридж). University Press, стр. 9. ISBN. 978-0-521-58807-2.) - ^ Рольфсен, Дейл (1976). Узлы и ссылки . Опубликовать или погибнуть. ISBN 978-0-914098-16-4.
- ^ "Диаграмма Венна". Архивировано 01ноября 2009 г.в WebCite , Encarta World English Dictionary, North American Edition 2007. Архивировано 01.11.2009.
- ^ Кларенс Ирвинг Льюис (1918). Обзор символической логики . Частично переиздано Dover в 1960 г. с. 157.
Дальнейшее чтение [ править ]
- Баркер-Пламмер, Дэйв; Бейлин, Сидней К. (1997). «Роль диаграмм в математических доказательствах». Машинная графика и зрение . 6 (1): 25–56. 10.1.1.49.4712 . (Специальный выпуск о схематическом представлении и рассуждении).
- Баркер-Пламмер, Дэйв; Бейлин, Сидней К. (2001). «О практической семантике математических диаграмм». В Андерсоне, М. (ред.). Рассуждения с помощью схематических изображений . Springer Verlag . ISBN 978-1-85233-242-6. CiteSeerX : 10.1.1.30.9246 .
- Кидман, Г. (2002). «Точность математических диаграмм в учебных материалах». In Cockburn, A .; Нарди, Э. (ред.). Труды ПМЭ 26 . 3 . Университет Восточной Англии. С. 201–8.
- Кульпа, Зенон (2004). «О схематическом изображении математических знаний» . В Андреа Асперти; Банчерек, Гжегож; Трюбулец, Анджей (ред.). Управление математическими знаниями: третья международная конференция, MKM 2004, Беловежа, Польша, 19–21 сентября 2004 г .: Материалы . Springer. С. 191–204. ISBN 978-3-540-23029-8.
- Puphaiboon, K .; Вудкок, А .; Скривенер, С. (25 марта 2005 г.). «Методика построения математических диаграмм». In Bust, Philip D .; Маккейб, PT (ред.). Современная эргономика 2005 Труды Международной конференции по современной эргономике (CE2005) . Тейлор и Фрэнсис. ISBN 978-0-415-37448-4.
Внешние ссылки [ править ]
| Викискладе есть медиафайлы, связанные с математическими диаграммами . |
- «Диаграммы» . Стэнфордская энциклопедия философии . Осень 2008 г.
- Кульпа, Зенон . «Диаграмматика: искусство мышления с помощью диаграмм» . Архивировано из оригинального 25 апреля 2013 года .
- Одна из старейших сохранившихся диаграмм от Евклида Отто Нойгебауэра.
- Ломас, Деннис (1998). «Диаграммы в математическом образовании: философская оценка» . Философия образования общества. Архивировано из оригинала на 2011.