В теории категорий моноидальные функторы - это функторы между моноидальными категориями, сохраняющие моноидальную структуру. Более конкретно, моноидальный функтор между двумя моноидальными категориями состоит из функтора между категориями вместе с двумя отображениями когерентности - естественным преобразованием и морфизмом, которые сохраняют моноидальное умножение и единицу соответственно. Математики требуют, чтобы эти карты согласованности удовлетворяли дополнительным свойствам в зависимости от того, насколько строго они хотят сохранить моноидальную структуру; каждое из этих свойств приводит к несколько иному определению моноидальных функторов
- Карты когерентности нестрогих моноидальных функторов не обладают дополнительными свойствами; они не обязательно обратимы.
- Карты когерентности сильных моноидальных функторов обратимы.
- Карты когерентности строгих моноидальных функторов являются тождественными.
Хотя здесь мы проводим различие между этими разными определениями, авторы могут называть любой из этих просто моноидальных функторов .
Определение [ править ]
Позвольте и быть моноидальными категориями. Слабые моноидальный функтор из к (который также может быть просто называется моноидалъное функтор) состоит из функтора вместе с естественным преобразованием
между функторами и морфизмом
- ,
называются карты когерентности или структурные морфизмы , которые являются такими , что для каждых трех объектов , и из диаграмм
коммутирую в категории . Выше, различные естественные преобразования, обозначенные с помощью, являются частями моноидальной структуры на и .
Варианты [ править ]
- Двойственный к моноидальному функтору является комоноидальным функтором ; это моноидальный функтор, отображения когерентности которого обращены. Комоноидальные функторы также могут называться опмоноидальными, моноидальными функциями colax или моноидальными функторами oplax.
- Сильный моноидальный функтор является моноидальным функтор которого когерентность карты обратимы.
- Строгий моноидальный функтор является моноидальным функтор когерентности которых карта идентичность.
- Плетеный моноидальный функтор является моноидальным функтором между плетеной моноидальной категорией (с оплеткой обозначается ) таким образом, что следующая диаграмма коммутирует для каждой пары объектов , Б в :
- Симметричный моноидальный функтор является плетеным моноидальным функтором, области и область значений являются симметричными моноидальными категориями .
Примеры [ править ]
- Базовый функтор из категории абелевых групп в категорию множеств. В этом случае карта отправляет (a, b) в ; карта отправляется в 1.
- Если - (коммутативное) кольцо, то свободный функтор продолжается до сильно моноидального функтора (а также, если он коммутативен).
- Если - гомоморфизм коммутативных колец, то функтор ограничения моноидален, а функтор индукции сильно моноидален.
- Важным примером симметричного моноидального функтора является недавно разработанная математическая модель топологической квантовой теории поля . Пусть будет категория кобордизмы из п-1, п - мерных многообразий с тензорным произведением дается несвязным объединением и блоком пустого коллектора. Топологическая квантовая теория поля в размерности n - это симметричный моноидальный функтор
- Гомологии функтор моноидальный , как через карту .
Свойства [ править ]
- Если является моноидным объектом в , то является моноидным объектом в .
Моноидальные функторы и присоединения [ править ]
Предположим, что функтор сопряжен слева к моноидалу . Тогда имеет комоноидальную структуру, индуцированную , определяемую
и
- .
Если индуцированная структура на сильной, то единица и счетчик присоединения являются моноидальными естественными преобразованиями , а присоединение называется моноидальным присоединением ; наоборот, левый сопряженный к моноидальному присоединению всегда сильный моноидальный функтор.
Аналогично, правый сопряженный к комоноидальному функтору является моноидальным, а правый сопряженный к комоноидальному функтору является сильным моноидальным функтором.
См. Также [ править ]
Ссылки [ править ]
- Келли, Г. Макс (1974), "Доктринальное присоединение" , конспект лекций по математике , 420 , 257–280











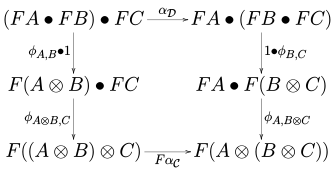





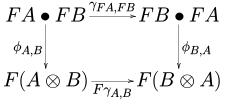














![{\ displaystyle (Ch (R {\ mathsf {-mod}}), \ otimes, R [0]) \ to (grR {\ mathsf {-mod}}, \ otimes, R [0])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b5b3f3ab1c1e64cb4bc1848cedd0ae03b5e833f)
![{\ displaystyle H _ {\ ast} (C_ {1}) \ otimes H _ {\ ast} (C_ {2}) \ to H _ {\ ast} (C_ {1} \ otimes C_ {2}), [x_ { 1}] \ otimes [x_ {2}] \ mapsto [x_ {1} \ otimes x_ {2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88c1233008efff53b6dd10c40d0c790e60440b6c)








