Принцип ортогональности

В статистике и обработке сигналов , то принцип ортогональности является необходимым и достаточным условием оптимальности оценки байесовской . В общих чертах принцип ортогональности гласит, что вектор ошибок оптимальной оценки (в смысле среднеквадратичной ошибки ) ортогонален любой возможной оценке. Принцип ортогональности чаще всего формулируется для линейных оценок, но возможны и более общие формулировки. Поскольку этот принцип является необходимым и достаточным условием оптимальности, его можно использовать для поиска оценки минимальной среднеквадратичной ошибки .

Принцип ортогональности для линейных оценщиков [ править ]

Принцип ортогональности чаще всего используется при линейной оценке. ^[1] В этом контексте пусть x будет неизвестным случайным вектором, который должен быть оценен на основе вектора наблюдения y . Хочется построить линейную оценку для некоторой матрицы H и вектора c . Тогда принцип ортогональности гласит, что оценщик достигает минимальной среднеквадратичной ошибки тогда и только тогда, когда${\ displaystyle {\ hat {x}} = Hy + c}$${\ displaystyle {\ hat {x}}}$

• ${\ displaystyle \ operatorname {E} \ {({\ hat {x}} - x) y ^ {T} \} = 0,}$ и
• ${\ displaystyle \ operatorname {E} \ {{\ hat {x}} - x \} = 0.}$

Если x и y имеют нулевое среднее значение, тогда достаточно потребовать первого условия.

Пример [ править ]

Предположим, что x - гауссовская случайная величина со средним m и дисперсией. Также предположим, что мы наблюдаем значение, где w - гауссовский шум, который не зависит от x и имеет среднее значение 0 и дисперсию. Мы хотим найти линейную оценку, минимизирующую MSE. Подставляя выражение в два требования принципа ортогональности, получаем${\ displaystyle \ sigma _ {x} ^ {2}.}$${\displaystyle y=x+w,}$${\displaystyle \sigma _{w}^{2}.}$${\displaystyle {\hat {x}}=hy+c}$${\displaystyle {\hat {x}}=hy+c}$

${\displaystyle 0=\operatorname {E} \{({\hat {x}}-x)y\}}$

${\displaystyle 0=\operatorname {E} \{(hx+hw+c-x)(x+w)\}}$

${\displaystyle 0=h(\sigma _{x}^{2}+\sigma _{w}^{2})+hm^{2}+cm-\sigma _{x}^{2}-m^{2}}$

и

${\displaystyle 0=\operatorname {E} \{{\hat {x}}-x\}}$

${\displaystyle 0=\operatorname {E} \{hx+hw+c-x\}}$

${\displaystyle 0=(h-1)m+c.}$

Решение этих двух линейных уравнений для h и c приводит к

${\displaystyle h={\frac {\sigma _{x}^{2}}{\sigma _{x}^{2}+\sigma _{w}^{2}}},\quad c={\frac {\sigma _{w}^{2}}{\sigma _{x}^{2}+\sigma _{w}^{2}}}m,}$

так что линейная оценка минимальной среднеквадратичной ошибки определяется выражением

${\displaystyle {\hat {x}}={\frac {\sigma _{x}^{2}}{\sigma _{x}^{2}+\sigma _{w}^{2}}}y+{\frac {\sigma _{w}^{2}}{\sigma _{x}^{2}+\sigma _{w}^{2}}}m.}$

Эту оценку можно интерпретировать как средневзвешенное значение между зашумленными измерениями y и предыдущим ожидаемым значением m . Если дисперсия шума мала по сравнению с дисперсией предшествующего (соответствующего высокому SNR ), то большая часть веса придается измерениям y , которые считаются более надежными, чем априорная информация. И наоборот, если дисперсия шума относительно выше, тогда оценка будет близка к m , поскольку измерения недостаточно надежны, чтобы перевесить априорную информацию.${\displaystyle \sigma _{w}^{2}}$${\displaystyle \sigma _{x}^{2}}$

Наконец, обратите внимание, что, поскольку переменные x и y вместе являются гауссовскими, оценка минимальной MSE является линейной. ^[2] Следовательно, в этом случае описанная выше оценка минимизирует MSE среди всех оценок, а не только линейных оценок.

Общая формулировка [ править ]

Позвольте быть гильбертовым пространством случайных величин со скалярным продуктом, определенным . Предположим , это замкнутое подпространство , представляющее пространство всех возможных оценок. Хочется найти вектор, который аппроксимирует вектор . Точнее, хотелось бы минимизировать среднеквадратичную ошибку (MSE) между и .${\displaystyle V}$${\displaystyle \langle x,y\rangle =\operatorname {E} \{x^{H}y\}}$${\displaystyle W}$${\displaystyle V}$${\displaystyle {\hat {x}}\in W}$${\displaystyle x\in V}$${\displaystyle \operatorname {E} \|x-{\hat {x}}\|^{2}}$${\displaystyle {\hat {x}}}$${\displaystyle x}$

В частном случае линейных оценок, описанных выше, пространство - это набор всех функций от и , а набор линейных оценок, т. Е. Линейных функций только от. Другие параметры, которые могут быть сформулированы таким образом, включают подпространство причинных линейных фильтров и подпространство всех (возможно, нелинейных) оценок.${\displaystyle V}$${\displaystyle x}$${\displaystyle y}$${\displaystyle W}$${\displaystyle y}$

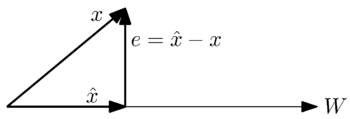
Геометрически мы можем увидеть эту проблему в следующем простом случае, когда - одномерное подпространство:${\displaystyle W}$

Мы хотим найти наиболее близкое приближение к вектору вектором в пространстве . Из геометрической интерпретации интуитивно понятно, что наилучшее приближение или наименьшая ошибка возникает, когда вектор ошибки ортогонален векторам в пространстве . ${\displaystyle x}$${\displaystyle {\hat {x}}}$${\displaystyle W}$${\displaystyle e}$${\displaystyle W}$

Точнее, общий принцип ортогональности утверждает следующее: для данного замкнутого подпространства оценок в гильбертовом пространстве и элемента в элементе достигается минимальная MSE среди всех элементов в том и только тогда, когда для всех${\displaystyle W}$${\displaystyle V}$${\displaystyle x}$${\displaystyle V}$${\displaystyle {\hat {x}}\in W}$${\displaystyle W}$${\displaystyle \operatorname {E} \{(x-{\hat {x}})y^{T}\}=0}$${\displaystyle y\in W.}$

Сформулированный таким образом, этот принцип является просто формулировкой проекционной теоремы Гильберта . Тем не менее, широкое использование этого результата в обработке сигналов привело к названию «принцип ортогональности».

Решение проблем минимизации ошибок [ править ]

Ниже приводится один из способов найти оценку минимальной среднеквадратичной ошибки с использованием принципа ортогональности.

Мы хотим иметь возможность аппроксимировать вектор с помощью ${\displaystyle x}$

${\displaystyle x={\hat {x}}+e\,}$

куда

${\displaystyle {\hat {x}}=\sum _{i}c_{i}p_{i}}$

представляет собой приближение как линейную комбинацию векторов в подпространстве, охватываемом Следовательно, мы хотим иметь возможность найти коэффициенты , чтобы мы могли записать наше приближение в известных терминах.${\displaystyle x}$${\displaystyle W}$${\displaystyle p_{1},p_{2},\ldots .}$${\displaystyle c_{i}}$

По теореме ортогональности, квадрат нормы вектора ошибки, , сводится к минимуму , когда для всех J ,${\displaystyle \left\Vert e\right\Vert ^{2}}$

${\displaystyle \left\langle x-\sum _{i}c_{i}p_{i},p_{j}\right\rangle =0.}$

Развивая это уравнение, получаем

${\displaystyle \left\langle x,p_{j}\right\rangle =\left\langle \sum _{i}c_{i}p_{i},p_{j}\right\rangle =\sum _{i}c_{i}\left\langle p_{i},p_{j}\right\rangle .}$

Если имеется конечное число векторов , можно записать это уравнение в матричной форме как${\displaystyle n}$${\displaystyle p_{i}}$

${\displaystyle {\begin{bmatrix}\left\langle x,p_{1}\right\rangle \\\left\langle x,p_{2}\right\rangle \\\vdots \\\left\langle x,p_{n}\right\rangle \end{bmatrix}}={\begin{bmatrix}\left\langle p_{1},p_{1}\right\rangle &\left\langle p_{2},p_{1}\right\rangle &\cdots &\left\langle p_{n},p_{1}\right\rangle \\\left\langle p_{1},p_{2}\right\rangle &\left\langle p_{2},p_{2}\right\rangle &\cdots &\left\langle p_{n},p_{2}\right\rangle \\\vdots &\vdots &\ddots &\vdots \\\left\langle p_{1},p_{n}\right\rangle &\left\langle p_{2},p_{n}\right\rangle &\cdots &\left\langle p_{n},p_{n}\right\rangle \end{bmatrix}}{\begin{bmatrix}c_{1}\\c_{2}\\\vdots \\c_{n}\end{bmatrix}}.}$

Предполагая , являются линейно независимыми , то Определитель Грама можно инвертировать с получением${\displaystyle p_{i}}$

${\displaystyle {\begin{bmatrix}c_{1}\\c_{2}\\\vdots \\c_{n}\end{bmatrix}}={\begin{bmatrix}\left\langle p_{1},p_{1}\right\rangle &\left\langle p_{2},p_{1}\right\rangle &\cdots &\left\langle p_{n},p_{1}\right\rangle \\\left\langle p_{1},p_{2}\right\rangle &\left\langle p_{2},p_{2}\right\rangle &\cdots &\left\langle p_{n},p_{2}\right\rangle \\\vdots &\vdots &\ddots &\vdots \\\left\langle p_{1},p_{n}\right\rangle &\left\langle p_{2},p_{n}\right\rangle &\cdots &\left\langle p_{n},p_{n}\right\rangle \end{bmatrix}}^{-1}{\begin{bmatrix}\left\langle x,p_{1}\right\rangle \\\left\langle x,p_{2}\right\rangle \\\vdots \\\left\langle x,p_{n}\right\rangle \end{bmatrix}},}$

таким образом обеспечивая выражение для коэффициентов оценки минимальной среднеквадратичной ошибки.${\displaystyle c_{i}}$

См. Также [ править ]

• Минимальная среднеквадратичная ошибка
• Теорема Гильберта о проекции

Заметки [ править ]

Ссылки [ править ]

• Кей, С.М. (1993). Основы статистической обработки сигналов: теория оценивания . Прентис Холл. ISBN 0-13-042268-1.
• Луна, Тодд К. (2000). Математические методы и алгоритмы обработки сигналов . Прентис-Холл. ISBN 0-201-36186-8.