Радикальная ось

Рис. 1. Иллюстрация радикальной оси (красная линия) двух заданных окружностей (сплошной черный). Для любой точки P (синяя) на радикальной оси может быть нарисован уникальный круг (пунктирный) с центром в этой точке и пересекающий обе заданные окружности под прямым углом, т. Е. Ортогонально, в точках, где касательные от P касаются круги. Точка P имеет одинаковую мощность по отношению к обеим заданным окружностям, поскольку касательные от точки P (синие линии) являются радиусами ортогональной окружности и, следовательно, имеют одинаковую длину.

В геометрии радикальная ось двух неконцентрических окружностей - это линия, образованная двумя окружностями, перпендикулярная линии, соединяющей центры окружностей. Если круги пересекаются, их радикальная ось - это линия, проходящая через их две точки пересечения, а если они касаются , это их линия касания. Для двух непересекающихся окружностей радикальная ось - это геометрическое место точек, в которых касательные, проведенные к обеим окружностям, имеют одинаковую длину.

Независимо от того, пересекаются ли две определяющие окружности, касаются ли они или не пересекаются, их радикальная ось является геометрическим местом точек, мощность которых по отношению к двум окружностям одинакова. По этой причине радикальную ось также называют линией питания или биссектрисой двух окружностей. Степень точки относительно круга - это квадрат евклидова расстояния от точки до центра круга за вычетом квадрата радиуса круга. Для точки вне круга ее мощность - положительное число, радиус другого круга с центром в котором пересекает ${\ displaystyle p}$ ${\ displaystyle C}$ ${\ displaystyle p}$ ${\ displaystyle C}$ под прямым углом. Следовательно, точки радикальной оси, которые находятся за пределами ее определяющих окружностей, являются центрами окружностей, которые пересекают обе определяющие окружности под прямым углом. ^[1]

В общем, любые две непересекающиеся неконцентрические окружности могут быть выровнены с окружностями системы биполярных координат . В этом случае радикальная ось - это просто ось этой системы координат. Каждая окружность на оси, проходящая через два фокуса системы координат, пересекает две окружности ортогонально. Коллекция максимальны окружности, все имеющие центры на данную линию и все пары , имеющие ту же самую радикальную ось, известны как карандаш из коаксиальных кругов . ${\ displaystyle y}$

Если две окружности пересекаются, радикальная ось - это секущая линия, соответствующая их общей хорде .

Рисунок 2: Радикальный центр (оранжевая точка) - это центр уникального круга (также оранжевого), который пересекает три заданных круга под прямым углом.

Радикальный центр трех кругов [ править ]

Рассмотрим три окружности A , B и C , никакие две из которых не являются концентрическими. Теорема радикальной оси утверждает, что три радикальные оси (для каждой пары окружностей) пересекаются в одной точке, называемой радикальным центром , или параллельны. ^[2] Говоря техническим языком, три радикальные оси параллельны (имеют общую точку); если они параллельны, они совпадают в бесконечности.

Простое доказательство состоит в следующем. ^[3] Радикальная ось окружностей A и B определяется как линия, вдоль которой касательные к этим окружностям равны по длине a = b . Точно так же касательные к окружностям B и C должны быть равны по длине на их радикальной оси. К транзитивности из равенства , все три касательных равны = Ь = с в точке пересечения г этих двух радикальных осей. Следовательно, радикальная ось для окружностей A и C должна проходить через одну и ту же точкуr , так как там a = c . Эта общая точка пересечения r является радикальным центром .

Это уникальный круг с центром в радикальном центре, который ортогонален всем трем окружностям. Это следует также из транзитивности, потому что каждая радикальная ось, являющаяся геометрическим местом центров окружностей, которые ортогонально разрезают каждую пару данных окружностей, требует, чтобы все три окружности имели равный радиус на пересечении всех трех осей.

Геометрическое построение [ править ]

Конструкция радикальной оси

Радикальную ось двух окружностей A и B можно построить, проведя линию через любые две точки на оси. Точку на оси можно найти, нарисовав круг C, который пересекает оба круга A и B в двух точках. Эти две линии , проходящие через каждую пару точек пересечения являются радикальные оси А и С , и из B и C . Эти две прямые пересекаются в точке J, которая является радикальным центром всех трех окружностей, как описано выше ; следовательно, эта точка также лежит на радикальной оси A и B. Повторяя этот процесс с другим таким кругом D обеспечивает вторую точку K . Радикальная ось линия , проходящая через оба J и K .

Рисунок 3: Линии, проходящие через соответствующие антигомологические точки, пересекаются на радикальной оси двух данных окружностей (зеленой и синей с центрами в точках C и D соответственно). Точки P и Q являются antihomologous, так же как S и T . Эти четыре точки лежат на окружности, которая пересекает две заданные окружности.

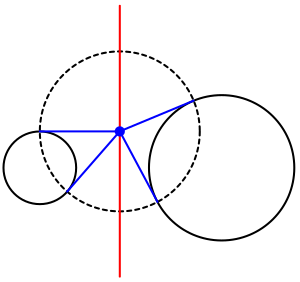
Частный случай этого подхода, показанный на рисунке 3, осуществляется с использованием антигомологических точек из внутреннего или внешнего центра подобия. Рассмотрим два луча , исходящие от внешнего центра гомотетическом E . Обозначим антигомологические пары точек пересечения этих лучей с двумя заданными окружностями как P и Q , а также S и T соответственно. Эти четыре точки лежат на общей окружности, которая пересекает две заданные окружности в двух точках каждая. ^[4] Следовательно, две прямые, соединяющие P и S , а также Q и Tпересекаются в радикальном центре трех окружностей, который лежит на радикальной оси данных окружностей. ^[5] Точно так же прямая, соединяющая две антигомологические точки на отдельных окружностях и их касательные, образуют равнобедренный треугольник, причем обе касательные имеют одинаковую длину. ^[6] Следовательно, такие касательные пересекаются на радикальной оси. ^[5]

Алгебраическое построение [ править ]

Рисунок 4: Алгебраическое определение радикальной оси. L - это расстояние от J до K , тогда как x ₁ и x ₂ - расстояния от K до B и от K до V соответственно. Переменные d ₁ и d ₂ представляют расстояния от J до B и от J до V , соответственно.

Ссылаясь на фиг.4, радикальная ось (красная) перпендикулярна синему отрезку прямой, соединяющему центры B и V двух данных окружностей, и пересекает этот отрезок в точке K между двумя окружностями. Поэтому достаточно , чтобы найти расстояние х ₁ или х ₂ от K до B или V , соответственно, где х ₁ + х ₂ равен D , расстояние между B и V .

Рассмотрим точку J на радикальной оси, и пусть ее расстояния до B и V обозначены как d ₁ и d ₂ соответственно. Поскольку J должен иметь одинаковую степень по отношению к обеим окружностям, отсюда следует, что

{\ displaystyle d_ {1} ^ {2} -r_ {1} ^ {2} = d_ {2} ^ {2} -r_ {2} ^ {2}}

где r ₁ и r ₂ - радиусы двух данных окружностей. По теореме Пифагора расстояния d ₁ и d ₂ могут быть выражены через x ₁ , x ₂ и L , расстояние от J до K

{\ displaystyle L ^ {2} + x_ {1} ^ {2} -r_ {1} ^ {2} = L ^ {2} + x_ {2} ^ {2} -r_ {2} ^ {2} }

При отмене L ² на обеих сторонах уравнения, то уравнение можно записать

{\ displaystyle x_ {1} ^ {2} -x_ {2} ^ {2} = r_ {1} ^ {2} -r_ {2} ^ {2}}

Разделив обе части на D = x ₁ + x _2, получим уравнение

x_{1}-x_{2}={\frac {r_{1}^{2}-r_{2}^{2}}{D}}

Добавление этого уравнения к x ₁ + x ₂ = D дает формулу для x ₁

2x_{1}=D+{\frac {r_{1}^{2}-r_{2}^{2}}{D}}

Вычитание того же уравнения дает соответствующую формулу для x ₂

2x_{2}=D-{\frac {r_{1}^{2}-r_{2}^{2}}{D}}

Детерминантный расчет [ править ]

Если окружности представить в трехлинейных координатах обычным образом, то их радикальный центр удобно задавать как некоторый определитель. В частности, пусть X = x : y : z обозначает переменную точку в плоскости треугольника ABC со сторонами a = | BC |, b = | CA |, c = | AB |, и изобразим круги следующим образом:

( dx + ey + fz ) ( ax + by + cz ) + g ( ayz + bzx + cxy ) = 0

( hx + iy + jz ) ( ax + by + cz ) + k ( ayz + bzx + cxy ) = 0

( lx + my + nz ) ( ax + by + cz ) + p ( ayz + bzx + cxy ) = 0

Тогда радикальный центр - это точка

\det {\begin{bmatrix}g&k&p\\e&i&m\\f&j&n\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\f&j&n\\d&h&l\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\d&h&l\\e&i&m\end{bmatrix}}.

Радикальная плоскость и гиперплоскость [ править ]

Радикальная плоскость два неконцентрических сфер в трех измерениях определяются аналогично: оно представляет собой геометрическое место точек , из которых касательные к двум сферам имеют одинаковую длину. ^[7] Тот факт, что это геометрическое место является плоскостью, следует из поворота в третьем измерении из того факта, что радикальная ось является прямой линией.

То же определение может быть применено к гиперсферам в евклидовом пространстве любой размерности, давая радикальную гиперплоскость двух неконцентрических гиперсфер.

Заметки [ править ]

↑ Джонсон (1960), стр. 31–32.
↑ Джонсон (1960), стр. 32–33.
^ Джонсон (1960), стр. 32.
↑ Джонсон (1960), стр. 20–21.
^ a b Джонсон (1960), стр. 41.
^ Джонсон (1960), стр. 21.
^ См. Онлайн-словарь Merriam – Webster .

Ссылки [ править ]

Р. А. Джонсон (1960). Продвинутая евклидова геометрия: элементарный трактат о геометрии треугольника и круга (перепечатка издания 1929 г., изд. Houghton Miflin). Нью-Йорк: Dover Publications. стр. 31 -43. ISBN 978-0-486-46237-0.

Дальнейшее чтение [ править ]

К. Стэнли Огилви (1990). Экскурсии по геометрии . Дувр. С. 17–23 . ISBN 0-486-26530-7.
HSM Coxeter , SL Greitzer (1967). Возвращение к геометрии . Вашингтон, округ Колумбия : Математическая ассоциация Америки . стр. 31 -36, 160-161. ISBN 978-0-88385-619-2.
Кларк Кимберлинг, «Центры треугольников и центральные треугольники», Congressus Numerantium 129 (1998) i – xxv, 1–295.

Внешние ссылки [ править ]

Викискладе есть медиафайлы по теме радикальных топоров .

Вайсштейн, Эрик В. «Радикальная линия» . MathWorld .
Вайсштейн, Эрик В. "Хордовая теорема" . MathWorld .
Анимация в Cut-the knot

[1] Джонсон (1960), стр. 31–32.

[2] Джонсон (1960), стр. 32–33.

[3] Джонсон (1960), стр. 32.

[4] Джонсон (1960), стр. 20–21.

[Johnson_1960,_p._41-5] Джонсон (1960), стр. 41.

[6] Джонсон (1960), стр. 21.

[7] См. Онлайн-словарь Merriam – Webster .

[1]