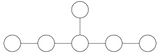
Диаграмма Дынкина
В математической области теории Ли диаграмма Дынкина , названная в честь Юджина Дынкина , представляет собой тип графа с удвоенными или утроенными ребрами (нарисованными в виде двойной или тройной линии). Диаграммы Дынкина возникают при классификации полупростых алгебр Ли над алгебраически замкнутыми полями , при классификации групп Вейля и других конечных групп отражения и в других контекстах. Различные свойства диаграммы Дынкина (например, содержит ли она несколько ребер или ее симметрии) соответствуют важным особенностям ассоциированной алгебры Ли.
Термин «диаграмма Дынкина» может быть неоднозначным. В некоторых случаях диаграммы Дынкина предполагаются направленными , и в этом случае они соответствуют системам корней и полупростым алгебрам Ли, а в других случаях они предполагаются неориентированными , и в этом случае они соответствуют группам Вейля. В этой статье «диаграмма Дынкина» означает направленную диаграмму Дынкина, а неориентированные диаграммы Дынкина будут называться так явно.
Фундаментальный интерес к диаграммам Дынкина состоит в том, что они классифицируют полупростые алгебры Ли над алгебраически замкнутыми полями . Такие алгебры Ли классифицируются через их корневую систему , которая может быть представлена диаграммой Дынкина. Затем диаграммы Дынкина классифицируют в соответствии с ограничениями, которым они должны удовлетворять, как описано ниже.
Отбрасывание направления на ребрах графа соответствует замене системы корней конечной группой отражения, которую она порождает, так называемой группой Вейля , и, таким образом, неориентированные диаграммы Дынкина классифицируют группы Вейля.
Они имеют следующее соответствие для алгебр Ли, связанных с классическими группами над комплексными числами:
Для исключительных групп названия алгебры Ли и связанной с ней диаграммы Дынкина совпадают.