Тонкий треугольник

Рис.1 Равнобедренный тонкий треугольник

Тощий треугольник в тригонометрии треугольник, высота которого намного больше , чем его основание. Решение таких треугольников может быть значительно упрощена путем использования приближения , что синус малого угла равен углу в радианах . Решение особенно просто для тонких треугольников, которые также являются равнобедренными или прямоугольными : в этих случаях можно полностью отказаться от тригонометрических функций или таблиц.

Тонкий треугольник находит применение в геодезии, астрономии и стрельбе.

Равнобедренный треугольник [ править ]

Таблица ошибок синусоидальной малоугловой аппроксимации ^[1]

Большие углы

Маленькие углы

угол		ошибка
(градусы)	(радианы)	(%)
1	0,017	0,005
2	0,035	0,02
5	0,087	0,13
10	0,175	0,51
15	0,262	1,15
20	0,349	2,06
25	0,436	3,25
30	0,524	4,72
35 год	0,611	6.50
40	0,698	8,61
45	0,785	11.07
50	0,873	13,92
55	0,960	17,19
60	1.047	20,92

угол		ошибка
(минут)	(радианы)	( частей на миллион )
1	0,0003	0,01
2	0,0006	0,06
5	0,0015	0,35
10	0,0029	1,41
15	0,0044	3,17
20	0,0058	5,64
25	0,0073	8,81
30	0,0087	12,69
35 год	0,0102	17,28
40	0,0116	22,56
45	0,0131	28,56
50	0,0145	35,26
55	0,0160	42,66
60	0,0175	50,77

Приблизительное решение для узкого равнобедренного треугольника, показанного на рисунке 1, есть;

{\ displaystyle b \ simeq r \ theta \,}

{\ displaystyle {\ text {area}} \ simeq {\ frac {1} {2}} \ theta r ^ {2} \,}

Это основано на малоугловых приближениях ;

{\ Displaystyle \ грех \ тета \ симек \ тета, \ квад \ тета \ 11 \,}

и,

{\ displaystyle \ cos \ theta = \ sin \ left ({\ frac {\ pi} {2}} - \ theta \ right) \ simeq 1, \ quad \ theta \ ll 1}

когда в радианах . ${\ Displaystyle \ scriptstyle \ theta}$

Доказательство решения тонкого треугольника следует из малоуглового приближения с применением закона синусов . Снова обращаясь к фиг.1;

{\ displaystyle {\ frac {b} {\ sin \ theta}} = {\ frac {r} {\ sin \ left ({\ frac {\ pi - \ theta} {2}} \ right)}}}

Этот член представляет собой базовый угол треугольника и является этим значением, потому что сумма внутренних углов любого треугольника (в данном случае два базовых угла плюс θ ) равна π . Применение приближения малых углов к закону синусов выше приводит к: $\scriptstyle {\frac {\pi -\theta }{2}}$

{\frac {b}{\theta }}\simeq {\frac {r}{1}}

желаемый результат.

Рис.2 Длина дуги l приближается к длине хорды b с уменьшением угла θ.

Этот результат эквивалентен предположению, что длина основания треугольника равна длине дуги окружности радиуса r, пересеченной углом θ . Ошибка составляет 10% или меньше для углов меньше примерно 43 °, ^[2]^[3] и улучшается квадратично : когда угол уменьшается в $k раз$ , ошибка уменьшается на $k 2$ .

Формула стороны-угла-стороны для площади треугольника:

{\text{area}}={\frac {\sin \theta }{2}}r^{2}

Применение аппроксимации малых углов приводит к:

{\text{area}}\simeq {\frac {1}{2}}\theta r^{2}\,

Правый треугольник [ править ]

Рис.3 Правый тонкий треугольник

Таблица ошибок малоугловой аппроксимации касательной ^[1]

Большие углы

Маленькие углы

угол		ошибка
(градусы)	(радианы)	(%)
1	0,017	−0,01
5	0,087	-0,25
10	0,175	−1,02
15	0,262	−2,30
20	0,349	-4,09
25	0,436	−6,43
30	0,524	-9,31
35 год	0,611	-12,76
40	0,698	−16,80
45	0,785	−21,46
50	0,873	-26,77
55	0,960	-32,78
60	1.047	-39,54

угол		ошибка
(минут)	(радианы)	(частей на миллион)
1	0,0003	-0,03
5	0,0015	−0,71
10	0,0029	−2,82
15	0,0044	−6,35
20	0,0058	-11,28
25	0,0073	-17,63
30	0,0087	-25,38
35 год	0,0102	-34,55
40	0,0116	-45,13
45	0,0131	-57,12
50	0,0145	-70,51
55	0,0160	-85,32
60	0,0175	-101,54

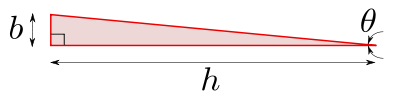
Приблизительное решение правого тонкого треугольника, показанного на рисунке 3, равно;

b\simeq h\theta

Это основано на малоугловом приближении;

\tan \theta \simeq \theta ,\quad \theta \ll 1

которые при подстановке в точное решение;

b=h\tan \theta \

дает желаемый результат.

Погрешность этого приближения составляет менее 10% для углов 31 ° или меньше. ^[4]

Приложения [ править ]

Применение тонкого треугольника происходит в любой ситуации, когда необходимо определить расстояние до удаленного объекта. Это может происходить в геодезии, астрономии, а также в военных целях.

Астрономия [ править ]

Тонкий треугольник часто используется в астрономии для измерения расстояния до объектов Солнечной системы . Основание треугольника образовано расстоянием между двумя измерительными станциями, а угол θ - это угол параллакса, образованный объектом, видимым двумя станциями. Эта базовая линия обычно очень длинная для лучшей точности; в принципе станции могут быть на противоположных сторонах Земли. Однако это расстояние все еще мало по сравнению с расстоянием до измеряемого объекта (высота треугольника), и решение тонкого треугольника может быть применено и по-прежнему обеспечивает высокую точность. Альтернативный метод измерения базовых углов теоретически возможен, но не так точен. Базовые углы очень близки к прямым, и их необходимо измерять с гораздо большей точностью, чем угол параллакса, чтобы получить такую же точность. ^[5]

Тот же метод измерения углов параллакса и применения тонкого треугольника можно использовать для измерения расстояний до звезд, по крайней мере, до ближайших. Однако в случае звезд обычно требуется более длинная базовая линия, чем диаметр Земли. Вместо использования двух станций на базовой линии, два измерения выполняются с одной и той же станции в разное время года. В течение промежуточного периода орбита Земли вокруг Солнца перемещает измерительную станцию на большое расстояние, обеспечивая очень длинную базовую линию. Длина этой базовой линии может быть равна большой оси земной орбиты или, что эквивалентно, двум астрономическим единицам (AU). Расстояние до звезды с углом параллакса всего одна угловая секундаизмеренная на базовой линии в одну а.е., является единицей, известной в астрономии как парсек (пк), и равна примерно 3,26 световых лет . ^[6] Существует обратная зависимость между расстоянием в парсеках и углом в угловых секундах. Например, две угловые секунды соответствуют расстоянию 0,5 пк, а 0,5 угловой секунды соответствуют расстоянию в два парсека. ^[7]

Стрельба [ править ]

Тонкий треугольник полезен при стрельбе, поскольку он позволяет рассчитывать взаимосвязь между дальностью и размером цели без необходимости стрелку вычислять или искать какие-либо тригонометрические функции . Военные и охотничьи прицелы часто имеют перекрестие калиброванный в миллирадианах , в этом контексте обычно называют просто мила или Mil-точки. Мишень высотой 1 метр и размером в 1 мил в прицеле соответствует дальности 1000 метров. Существует обратная зависимость между углом, измеренным в прицеле снайпера, и расстоянием до цели. Например, если размер этой же цели в прицеле составляет 2 мил, то дальность составляет 500 метров.^[8]

Еще одна единица измерения, которая иногда используется на прицелах, - это угловая минута (МОА). Расстояния, соответствующие угловым минутам, не являются точными числами в метрической системе, как в миллирадианах; однако существует удобное примерное соответствие целых чисел в британских единицах измерения . Мишень высотой 1 дюйм и размером 1 МОА в прицеле соответствует дальности 100 ярдов . ^[8] Или, что более полезно, цель высотой 6 футов и размером 4 MOA соответствует дальности 1800 ярдов (чуть больше мили).

Авиация [ править ]

Простая форма авиационной навигации, точный расчет , основывается на оценке скорости ветра на больших расстояниях для расчета желаемого курса. Поскольку прогнозируемая или сообщаемая скорость ветра редко бывает точной, необходимо регулярно корректировать курс самолета. Тонкие треугольники составляют основу правила 1 из 60 , которое гласит: «После 60 миль ваш курс отклоняется на один градус на каждую милю, которую вы отклоняетесь от курса». «60» очень близко к 180 / π = 57,30.

См. Также [ править ]

Бесконечно малые колебания маятника

Ссылки [ править ]

^ а б Васан, стр. 124
^ Abell et al. , стр. 414–415
^ Breithaupt, стр. 26
^ Holbrow et al. , стр. 30–31
^ Abell et al. , п. 414
^ Abell et al. , внутренняя передняя крышка
^ Abell et al. , стр. 414–416, 418–419
^ a b Варлоу, стр. 87

Библиография [ править ]

Джордж Огден Абелл, Дэвид Моррисон, Сидни К. Вольф, Исследование Вселенной , издательство Saunders College Pub., 1987 ISBN 0-03-005143-6 .
Джим Брайтхаупт, Физика для продвинутого уровня , Нельсон Торнс, 2000 ISBN 0-7487-4315-4 .
Чарльз Х. Холброу, Джеймс Н. Ллойд, Джозеф К. Амато, Энрике Гальвез, Бет Паркс, Современная вводная физика , Springer, 2010 ISBN 0-387-79079-9 .
Шрини Васан, Основы фотоники и оптики , издательство Trafford Publishing, 2004 ISBN 1-4120-4138-4 .
Том А. Варлоу, Огнестрельное оружие, закон и судебная баллистика , Taylor & Francis, 1996 ISBN 0-7484-0432-5 .

[Vasan124-1] а б Васан, стр. 124

[2] Abell et al. , стр. 414–415

[3] Breithaupt, стр. 26

[4] Holbrow et al. , стр. 30–31

[5] Abell et al. , п. 414

[6] Abell et al. , внутренняя передняя крышка

[7] Abell et al. , стр. 414–416, 418–419

[Warlow87-8] Варлоу, стр. 87

[1]