лемма Шпернера
В математике лемма Шпернера — комбинаторный результат о раскрасках триангуляций , аналогичный эквивалентной ей теореме Брауэра о неподвижной точке . [1] Он утверждает, что каждая шпернеровская раскраска (описанная ниже) триангуляции -мерного симплекса содержит клетку, все вершины которой окрашены в разные цвета.
Первоначальный результат такого рода был доказан Эмануэлем Шпернером в связи с доказательствами инвариантности области определения . Раскраски Шпернера использовались для эффективного вычисления фиксированных точек и в алгоритмах поиска корней , а также в алгоритмах справедливого деления (разрезания пирога). Нахождение раскраски Шпернера или, что то же самое, неподвижной точки Брауэра теперь считается неразрешимой вычислительной проблемой даже на плоскости в общем случае. Проблема в PPAD-complete , классе сложности, придуманном Christos Papadimitriou .
Согласно Советской математической энциклопедии (под ред. И. М. Виноградова ), родственная теорема 1929 г. ( Кнастера , Борсука и Мазуркевича ) также стала известна как лемма Шпернера — этот момент обсуждается в английском переводе (под ред. М. Хазевинкеля). Сейчас она широко известна как лемма Кнастера-Куратовского-Мазуркевича .
В одном измерении лемму Шпернера можно рассматривать как дискретную версию теоремы о промежуточном значении . В данном случае это, по сути, говорит о том, что если дискретная функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, то она должна переключать значения нечетное количество раз.
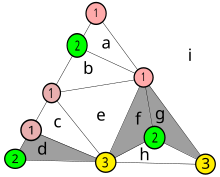
Разделите произвольно треугольник ABC на триангуляцию, состоящую из меньших треугольников, соприкасающихся ребром к ребру. Тогда шпернеровская раскраска триангуляции определяется как присвоение трех цветов вершинам триангуляции таким образом, что
Тогда каждая раскраска Шпернера каждой триангуляции имеет по крайней мере один «радужный треугольник», меньший треугольник в триангуляции, вершины которого окрашены во все три разных цвета. Точнее, радужных треугольников должно быть нечетное количество.