Многосеточный метод
В численном анализе многосеточный метод ( метод МГ ) — алгоритм решения дифференциальных уравнений с использованием иерархии дискретизаций . Они являются примером класса методов, называемых методами с несколькими разрешениями , которые очень полезны в задачах, демонстрирующих несколько масштабов поведения. Например, многие основные методы релаксации демонстрируют разную скорость сходимости для коротковолновых и длинноволновых компонентов, что предполагает разное обращение с этими разными масштабами, как в подходе анализа Фурье к многосеточному анализу. [1]Методы MG можно использовать как в качестве решателей, так и в качестве предобуславливателей .
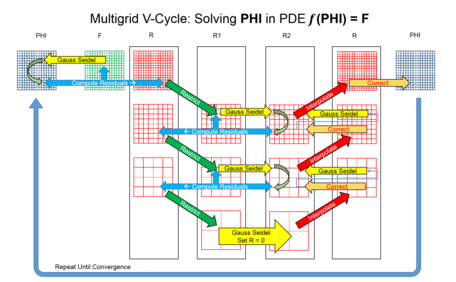
Основная идея многосеточного метода состоит в том, чтобы ускорить сходимость базового итерационного метода (известного как релаксация, который обычно уменьшает коротковолновую ошибку) за счет глобальной коррекции аппроксимации решения на мелкой сетке время от времени, достигаемой путем решения грубой задачи .. Грубая задача, несмотря на то, что ее решение дешевле, похожа на задачу с мелкой сеткой в том, что она также имеет коротковолновые и длинноволновые ошибки. Ее также можно решить, сочетая расслабление и обращение к еще более грубым сеткам. Этот рекурсивный процесс повторяется до тех пор, пока не будет достигнута сетка, где стоимость прямого решения пренебрежимо мала по сравнению со стоимостью одной релаксационной прогонки на мелкой сетке. Этот цикл с несколькими сетками обычно уменьшает все компоненты ошибки на фиксированную величину, значительно меньшую единицы, независимо от размера сетки с мелкой сеткой. Типичное применение многосеточного решения — численное решение эллиптических уравнений в частных производных в двух или более измерениях. [2]
Многосеточные методы могут применяться в сочетании с любым из распространенных методов дискретизации. Например, метод конечных элементов может быть преобразован в многосеточный метод. [3] В этих случаях многосеточные методы являются одними из самых быстрых методов решения, известных сегодня. В отличие от других методов, многосеточные методы являются общими в том смысле, что они могут обрабатывать произвольные области и граничные условия . Они не зависят от разделимости уравнений или других специальных свойств уравнения. Они также широко использовались для более сложных несимметричных и нелинейных систем уравнений, таких как уравнения упругости Ламе или уравнения Навье-Стокса .. [4]
Существует множество вариаций многосеточных алгоритмов, но общими чертами являются то, что рассматривается иерархия дискретизаций (сеток). Важные шаги: [5] [6]
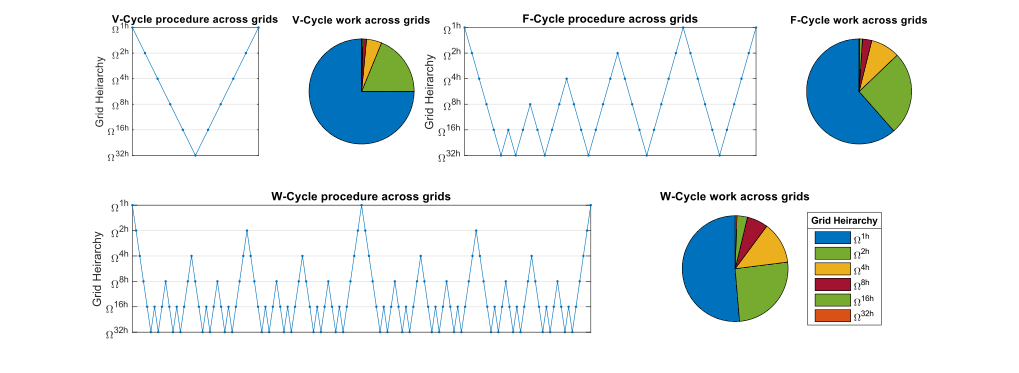
Существует множество вариантов многосеточных методов с различными компромиссами между скоростью решения одной итерации и скоростью сходимости с указанной итерацией. 3 основных типа: V-цикл, F-цикл и W-цикл. Для дискретной 2D-задачи F-цикл требует на 83 % больше времени для вычисления, чем итерация V-цикла, а итерация W-цикла занимает на 125 % больше времени. Если проблема возникает в трехмерной области, то итерация F-цикла и итерация W-цикла занимают примерно на 64 % и 75 % больше времени соответственно, чем итерация V-цикла без учета накладных расходов . Как правило, W-цикл обеспечивает сходимость, аналогичную F-циклу. Однако в случае задач конвекции-диффузии с большими числами Пекле, W-цикл может показать превосходство в скорости сходимости на итерацию по сравнению с F-циклом. Выбор операторов сглаживания чрезвычайно разнообразен, так как они включают методы подпространств Крылова и могут быть предобусловлены .
Любая итерация геометрического многосеточного цикла выполняется в иерархии сеток и, следовательно, может быть закодирована с использованием рекурсии. Поскольку функция вызывает себя с параметрами меньшего размера (более грубыми), рекурсия останавливается на самой грубой сетке. В случаях, когда система имеет высокое число обусловленности , процедура коррекции модифицируется таким образом, что на более мелкую сетку добавляется только часть пролонгированного решения на более грубой сетке.