Комплексное число

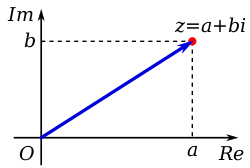
В математике комплексное число — это элемент системы счисления , который содержит действительные числа и определенный элемент, обозначаемый i , называемый мнимой единицей , и удовлетворяющий уравнению i ² = −1 . Более того, каждое комплексное число можно представить в виде a + bi , где a и b — действительные числа. Поскольку никакое действительное число не удовлетворяет приведенному выше уравнению, Рене Декарт назвал i мнимым числом . Для комплексного числа а+ bi , a называетсядействительная часть иbназываетсямнимая часть . Набор комплексных чисел обозначается одним из символовили C . Несмотря на историческую номенклатуру «мнимых», комплексные числа рассматриваются вматематических наукахстоль же «реальными», как и действительные числа, и являются основополагающими во многих аспектах научного описания мира природы. ^{[1] [а]}${\ Displaystyle \ mathbb {С}}$

Комплексные числа позволяют решать все полиномиальные уравнения , даже те, которые не имеют решений в действительных числах. Точнее, основная теорема алгебры утверждает, что каждое непостоянное полиномиальное уравнение с вещественными или комплексными коэффициентами имеет решение, представляющее собой комплексное число. Например, уравнение не имеет действительного решения, поскольку квадрат действительного числа не может быть отрицательным, но имеет два невещественных комплексных решения -1 + 3 i и -1 - 3 i .${\ Displaystyle (х + 1) ^ {2} = - 9}$

Сложение, вычитание и умножение комплексных чисел можно естественным образом определить с помощью правила i ² = −1 в сочетании с ассоциативным , коммутативным и дистрибутивным законами. Каждое ненулевое комплексное число имеет мультипликативное обратное . Это делает комплексные числа полем , в котором действительные числа являются подполем. Комплексные числа также образуют вещественное векторное пространство размерности два с {1, i } в качестве стандартного базиса .

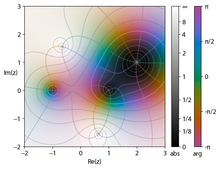
Этот стандартный базис делает комплексные числа декартовой плоскостью , называемой комплексной плоскостью . Это позволяет геометрическую интерпретацию комплексных чисел и их операций и, наоборот, выражать в терминах комплексных чисел некоторые геометрические свойства и конструкции. Например, действительные числа образуют действительную линию , которая отождествляется с горизонтальной осью комплексной плоскости. Комплексные числа с абсолютным значением один образуют единичный круг . Сложение комплексного числа — это сдвиг в комплексной плоскости, а умножение на комплексное число — это подобие с центром в начале координат. Комплексное сопряжение – этосимметричность отражения относительно действительной оси. Комплексное абсолютное значение является евклидовой нормой .

Таким образом, комплексные числа образуют богатую структуру, которая одновременно является алгебраически замкнутым полем , коммутативной алгеброй над действительными числами и евклидовым векторным пространством размерности два.

Комплексное число — это число формы a + bi , где a и b — действительные числа , а i — неопределенное число, удовлетворяющее i ² = −1 . Например, 2 + 3 i — комплексное число. ^[3]

Комплексное число можно визуально представить как пару чисел ( a ,  b ) , образующих вектор на диаграмме, называемой диаграммой Аргана , представляющей комплексную плоскость . Re — действительная ось, Im — воображаемая ось, а i — « воображаемая единица », удовлетворяющая условию i ² = −1 .

Иллюстрация комплексного числа z = x + iy на комплексной плоскости . Действительная часть — это x , а его мнимая часть — это y .

Комплексное число z в виде точки (черный) и ее вектор положения (синий)

Аргумент φ и модуль r определяют точку на комплексной плоскости.

График цветового круга выражения ( z ² - 1)( z - 2 - i ) ² / z ² + 2 + 2 i

Геометрическое представление z и его сопряженного z на комплексной плоскости

Сложение двух комплексных чисел можно выполнить геометрически, построив параллелограмм.

Умножение 2 + i (синий треугольник) и 3 + i (красный треугольник). Красный треугольник повернут так, чтобы совпасть с вершиной синего (суммирование обоих углов в членах φ ₁ + φ ₂ в уравнении) и растянут на длину гипотенузы синего треугольника (умножение обоих радиусов, согласно члену r ₁ r ₂ в уравнении).

Геометрическое представление корней со 2-го по 6-й комплексного числа z в полярной форме re ^iφ,  где r = | г  | и φ = arg z . Если z действительно, φ = 0 или π . Главные корни показаны черным цветом.

График цветового круга sin (1/ z ) . Черные части внутри относятся к числам, имеющим большие абсолютные значения.

Набор Мандельброта с помеченными реальной и мнимой осями.

Построение правильного пятиугольника с помощью линейки и циркуля .

Граф кватернионов Кэли Q8, показывающий циклы умножения на i , j и k