Внешняя алгебра
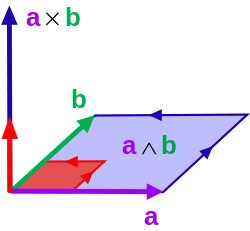
В математике внешнее произведение или клиновое произведение векторов — это алгебраическая конструкция, используемая в геометрии для изучения площадей , объемов и их многомерных аналогов. Внешний продукт двух векторов и , обозначаемый , называется бивектором и живет в пространстве, называемом внешним квадратом , векторном пространстве , отличном от исходного пространства векторов. Величину [ 3] можно интерпретировать как площадь параллелограмма со сторонами и , который в трех измерениях также можно вычислить с помощью перекрестного произведения двух векторов. В более общем смысле все параллельные плоские поверхности с одинаковой ориентацией и площадью имеют один и тот же бивектор как меру их ориентированной площади . Как и перекрестное произведение, внешнее произведение антикоммутативно , что означает, что для всех векторов и , но, в отличие от перекрестного произведения, внешнее произведение ассоциативно .
При таком рассмотрении внешнее произведение двух векторов называется 2-лезвием . В более общем смысле внешнее произведение любого числа k векторов может быть определено и иногда называется k -лезвием. Он живет в пространстве, известном как k -я внешняя сила. Величина получившегося k -лезвия представляет собой ориентированный гиперобъем k -мерного параллелоэдра , ребра которого являются заданными векторами, точно так же, как величина скалярного тройного произведения векторов в трех измерениях дает объем параллелепипеда, порожденного этими векторами.
Внешняя алгебра или алгебра Грассмана по Герману Грассману [ 4] — это алгебраическая система, продуктом которой является внешний продукт. Внешняя алгебра обеспечивает алгебраическую настройку, в которой можно отвечать на геометрические вопросы. Например, лезвия имеют конкретную геометрическую интерпретацию, а объектами внешней алгебры можно манипулировать в соответствии с набором недвусмысленных правил. Внешняя алгебра содержит объекты, являющиеся не только k -лезвиями, но и суммами k -лезвий; такая сумма называется k -вектором . [5 ] К-лопасти, поскольку они являются простыми произведениями векторов, называются простыми элементами алгебры. Ранг любого k -вектора определяется как наименьшее количество простых элементов, суммой которых он является. Внешний продукт продолжается до полной внешней алгебры, так что имеет смысл умножать любые два элемента алгебры. Оснащенная этим произведением, внешняя алгебра является ассоциативной алгеброй , что означает, что для любых элементов . k -векторы имеют степень k , что означает, что они являются суммами произведений k векторов. При перемножении элементов разных степеней степени складываются подобно умножению многочленов .. Это означает, что внешняя алгебра является градуированной алгеброй .