Вписанная и вневписанная окружности треугольника

А   треугольник с   incircle , Incenter ( ),${\ displaystyle I}$  Вневписанная, центры вневписанных окружностей ( , , ),${\ displaystyle J_ {A}}$${\ displaystyle J_ {B}}$${\displaystyle J_{C}}$  биссектрисы внутреннего угла и  биссектрисы внешнего угла. В  зеленый треугольник - эксцентральный треугольник.

В геометрии , то вписанная или вписанная окружность из треугольника является самым большим кругом , содержащийся в треугольнике; он касается ( касается ) трех сторон. Центр вписанной является треугольник центр под названием треугольника вписанной . ^[1]

Вневписанная или вневписанный круг ^[2] треугольник представляет собой окружность , лежащая вне треугольника, касательная к одной из его сторон и касательной к продолжениям двух другихов . В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника. ^[3]

Центр вписанной окружности, называемый центром , можно найти как пересечение трех биссектрис внутреннего угла . ^{[3] [4]} Центр вневписанной окружности - это пересечение внутренней биссектрисы одного угла (например, в вершине ) и внешних биссектрис двух других. Центр этого вневписанное называется эксцентрик относительно вершины , или эксцентриком из . ^[3] Поскольку внутренняя биссектриса угла перпендикулярна его внешней биссектрисе, из этого следует, что центр вписанной окружности вместе с тремя центрами вневписанной окружности образуют ортоцентрическую систему.${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$. ^{[5] : с. 182}

Все правильные многоугольники имеют касательные со всех сторон вписанные окружности, но не все многоугольники; те, что есть, являются касательными многоугольниками . См. Также Касательные линии к окружностям .

Incircle и центр [ править ]

Предположим, есть вписанная окружность с радиусом и центром . Позвольте быть длиной , длиной и длиной . Также позвольте , и быть точками касания , где вписанная окружность касается , и .${\displaystyle \triangle ABC}$${\displaystyle r}$${\displaystyle I}$${\displaystyle a}$${\displaystyle BC}$${\displaystyle b}$${\displaystyle AC}$${\displaystyle c}$${\displaystyle AB}$${\displaystyle T_{A}}$${\displaystyle T_{B}}$${\displaystyle T_{C}}$${\displaystyle BC}$${\displaystyle AC}$${\displaystyle AB}$

Incenter [ править ]

Вписанной является точкой , в которой внутренний угле биссектриса из соревнований.${\displaystyle \angle ABC,\angle BCA,{\text{ and }}\angle BAC}$

Расстояние от вершины до центра : ^{[ необходима ссылка ]}${\displaystyle A}$${\displaystyle I}$

${\displaystyle d(A,I)=c{\frac {\sin \left({\frac {B}{2}}\right)}{\cos \left({\frac {C}{2}}\right)}}=b{\frac {\sin \left({\frac {C}{2}}\right)}{\cos \left({\frac {B}{2}}\right)}}.}$

Трилинейные координаты [ править ]

Эти координаты трилинейных для точки в треугольнике есть отношение всех расстояний до сторон треугольника. Поскольку центр центра находится на одинаковом расстоянии от всех сторон треугольника, трилинейные координаты центра центра равны ^[6]

${\displaystyle \ 1:1:1.}$

Барицентрические координаты [ править ]

В барицентрических координатах для точки в треугольнике Дайте весы таким образом, что точка является взвешенным средним позиций треугольника вершин. Барицентрические координаты инцентратора даются ^{[ цитата ]}

${\displaystyle \ a:b:c}$

где , и - длины сторон треугольника, или, что то же самое (используя закон синусов ):${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\displaystyle \sin(A):\sin(B):\sin(C)}$

где , и - углы при трех вершинах.${\displaystyle A}$${\displaystyle B}$${\displaystyle C}$

Декартовы координаты [ править ]

В декартовы координаты из вписанной представляют собой взвешенное среднее значение координат вершин с использованием трех длины сторон треугольника по отношению к периметру (то есть, используя барицентрические координаты , приведенные выше, нормированные на сумму к единице) в качестве весов. Веса положительны, так что центр находится внутри треугольника, как указано выше. Если три вершины расположены на , и , и стороны противоположные этих вершин имеют соответствующие длины , и , затем вписанной находится ^{[ править ]}${\displaystyle (x_{a},y_{a})}$${\displaystyle (x_{b},y_{b})}$${\displaystyle (x_{c},y_{c})}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\displaystyle \left({\frac {ax_{a}+bx_{b}+cx_{c}}{a+b+c}},{\frac {ay_{a}+by_{b}+cy_{c}}{a+b+c}}\right)={\frac {a\left(x_{a},y_{a}\right)+b\left(x_{b},y_{b}\right)+c\left(x_{c},y_{c}\right)}{a+b+c}}.}$

Радиус [ править ]

Inradius вписанной в треугольнике со сторонами длиной , , задается ^[7]${\displaystyle r}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\displaystyle r={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}},}$ где ${\displaystyle s=(a+b+c)/2.}$

См . Формулу Герона .

Расстояния до вершин [ править ]

Обозначая центр как , расстояния от центра до вершин в сочетании с длинами сторон треугольника подчиняются уравнению ^[8]${\displaystyle \triangle ABC}$${\displaystyle I}$

${\displaystyle {\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1.}$

Кроме того, ^[9]

${\displaystyle IA\cdot IB\cdot IC=4Rr^{2},}$

где и - радиус описанной окружности и внутренний радиус треугольника соответственно.${\displaystyle R}$${\displaystyle r}$

Другие свойства [ править ]

Совокупность центров треугольников может быть задана структурой группы при покоординатном умножении трилинейных координат; в этой группе стимул образует элемент идентичности . ^[6]

Вложенная окружность и ее свойства радиуса [ править ]

Расстояния между вершиной и ближайшими точками касания [ править ]

Расстояния от вершины до двух ближайших точек касания равны; например: ^[10]

${\displaystyle d\left(A,T_{B}\right)=d\left(A,T_{C}\right)={\frac {1}{2}}(b+c-a).}$

Другие свойства [ править ]

Предположим, что точки касания вписанной окружности делят стороны на длины и , и , и и . Тогда вписанная окружность имеет радиус ^[11]${\displaystyle x}$${\displaystyle y}$${\displaystyle y}$${\displaystyle z}$${\displaystyle z}$${\displaystyle x}$

${\displaystyle r={\sqrt {\frac {xyz}{x+y+z}}}}$

а площадь треугольника равна

${\displaystyle \Delta ={\sqrt {xyz(x+y+z)}}.}$

Если абсолютные высоты от длины сторон , и являются , , и , затем inradius одна треть гармонических среднего этих высот; то есть ^[12]${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$${\displaystyle h_{a}}$${\displaystyle h_{b}}$${\displaystyle h_{c}}$${\displaystyle r}$

${\displaystyle r={\frac {1}{{\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}}}.}$

Произведение радиуса вписанной и окружность радиуса треугольника со сторонами , и это ^{[5] : 189, # 298 (г)}${\displaystyle r}$${\displaystyle R}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\displaystyle rR={\frac {abc}{2(a+b+c)}}.}$

Некоторые соотношения между сторонами, радиусом вписанной окружности и радиусом описанной окружности: ^[13]

${\displaystyle {\begin{aligned}ab+bc+ca&=s^{2}+(4R+r)r,\\a^{2}+b^{2}+c^{2}&=2s^{2}-2(4R+r)r.\end{aligned}}}$

Любая линия, проходящая через треугольник, которая разделяет площадь треугольника и его периметр пополам, проходит через центр треугольника (центр вписанной окружности). Для любого треугольника их может быть один, два или три. ^[14]

Обозначая центр вписанной окружности как , имеем ^[15]${\displaystyle \triangle ABC}$${\displaystyle I}$

${\displaystyle {\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1}$

и ^{[16] : 121, # 84}

${\displaystyle IA\cdot IB\cdot IC=4Rr^{2}.}$

Радиус вписанной окружности не превышает одной девятой суммы высот. ^{[17] : 289}

Квадрат расстояния от вписанной к описанной окружности задается ^{[18] : 232}${\displaystyle I}$${\displaystyle O}$

${\displaystyle OI^{2}=R(R-2r)}$,

и расстояние от вписанного до центра из девяти точек окружности является ^{[18] : 232}${\displaystyle N}$

${\displaystyle IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R.}$

Центр находится в среднем треугольнике (вершины которого являются серединами сторон). ^{[18] : 233, лемма 1.}

Отношение к площади треугольника [ править ]

Радиус вписанной окружности связан с площадью треугольника. ^[19] Отношение площади вписанной окружности к площади треугольника меньше или равно , при этом равенство сохраняется только для равносторонних треугольников . ^[20]${\displaystyle {\tfrac {\pi }{3{\sqrt {3}}}}}$

Предположим, есть вписанная окружность с радиусом и центром . Позвольте быть длиной , длиной и длиной . Теперь вписанная окружность касается в какой-то точке , а значит, и права. Таким образом, радиус является высота из . Следовательно, имеет базовую длину и высоту , а также площадь . Точно так же имеет площадь и площадь . Поскольку эти три треугольника распадаются , мы видим, что область : ^{[ необходима цитата ]}${\displaystyle \triangle ABC}$${\displaystyle r}$${\displaystyle I}$${\displaystyle a}$${\displaystyle BC}$${\displaystyle b}$${\displaystyle AC}$${\displaystyle c}$${\displaystyle AB}$${\displaystyle AB}$${\displaystyle T_{C}}$${\displaystyle \angle AT_{C}I}$${\displaystyle T_{C}I}$${\displaystyle \triangle IAB}$${\displaystyle \triangle IAB}$${\displaystyle c}$${\displaystyle r}$${\displaystyle {\tfrac {1}{2}}cr}$${\displaystyle \triangle IAC}$${\displaystyle {\tfrac {1}{2}}br}$${\displaystyle \triangle IBC}$${\displaystyle {\tfrac {1}{2}}ar}$${\displaystyle \triangle ABC}$${\displaystyle \Delta {\text{ of }}\triangle ABC}$

${\displaystyle \Delta ={\frac {1}{2}}(a+b+c)r=sr,}$     и     ${\displaystyle r={\frac {\Delta }{s}},}$

где есть площадь и является его -полупериметром .${\displaystyle \Delta }$${\displaystyle \triangle ABC}$${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$

Для альтернативной формулы рассмотрим . Это прямоугольный треугольник, одна сторона которого равна, а другая - . То же верно и для . Большой треугольник состоит из шести таких треугольников, а его общая площадь составляет: ^{[ необходима цитата ]}${\displaystyle \triangle IT_{C}A}$${\displaystyle r}$${\displaystyle r\cot \left({\frac {A}{2}}\right)}$${\displaystyle \triangle IB'A}$

${\displaystyle \Delta =r^{2}\left(\cot \left({\frac {A}{2}}\right)+\cot \left({\frac {B}{2}}\right)+\cot \left({\frac {C}{2}}\right)\right).}$

Треугольник и точка Жергонна [ править ]

Треугольник , с${\displaystyle \triangle ABC}$  вписанная окружность   Incenter ( ),${\displaystyle I}$  контактный треугольник ( ) и${\displaystyle \triangle T_{A}T_{B}T_{C}}$  Точка Жергонна ( )${\displaystyle G_{e}}$

Gergonne треугольник (из ) определяются три из точек соприкосновения вписанных на трех сторонах. Обозначается противоположная точка касания и т. Д.${\displaystyle \triangle ABC}$${\displaystyle A}$${\displaystyle T_{A}}$

Этот треугольник Gergonne, , также известная как контактный треугольник или Intouch треугольник из . Его площадь ${\displaystyle \triangle T_{A}T_{B}T_{C}}$${\displaystyle \triangle ABC}$

${\displaystyle K_{T}=K{\frac {2r^{2}s}{abc}}}$

где , и являются областью, радиус вписанной и -полупериметр исходного треугольника, а , и побочные длины исходного треугольника. Это та же область, что и у треугольника касания . ^[21]${\displaystyle K}$${\displaystyle r}$${\displaystyle s}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

Три линии , и пересекаются в одной точке называются Gergonne точки , обозначаются как (или треугольник центр X ₇ ). Точка Жергонна лежит в открытом ортоцентроидном диске, проколотом в его собственном центре, и может быть любой точкой в ​​нем. ^[22]${\displaystyle AT_{A}}$${\displaystyle BT_{B}}$${\displaystyle CT_{C}}$${\displaystyle G_{e}}$

Точка Жергонна треугольника имеет ряд свойств, в том числе то, что она является симедианной точкой треугольника Жергонна. ^[23]

Трилинейные координаты для вершин треугольника касания задаются ^{[ ссылка ]}

• ${\displaystyle {\text{vertex}}\,T_{A}=0:\sec ^{2}\left({\frac {B}{2}}\right):\sec ^{2}\left({\frac {C}{2}}\right)}$
• ${\displaystyle {\text{vertex}}\,T_{B}=\sec ^{2}\left({\frac {A}{2}}\right):0:\sec ^{2}\left({\frac {C}{2}}\right)}$
• ${\displaystyle {\text{vertex}}\,T_{C}=\sec ^{2}\left({\frac {A}{2}}\right):\sec ^{2}\left({\frac {B}{2}}\right):0.}$

Трилинейные координаты для точки Жергонна даются ^{[ ссылка ]}

${\displaystyle \sec ^{2}\left({\frac {A}{2}}\right):\sec ^{2}\left({\frac {B}{2}}\right):\sec ^{2}\left({\frac {C}{2}}\right),}$

или, что то же самое, по закону синуса ,

${\displaystyle {\frac {bc}{b+c-a}}:{\frac {ca}{c+a-b}}:{\frac {ab}{a+b-c}}.}$

Excircles и excenters [ править ]

А   треугольник с   incircle , Incenter ),${\displaystyle I}$  Вневписанная, центры вневписанных окружностей ( , , ),${\displaystyle J_{A}}$${\displaystyle J_{B}}$${\displaystyle J_{C}}$  биссектрисы внутреннего угла и  биссектрисы внешнего угла. В  зеленый треугольник - эксцентральный треугольник.

Вневписанная или вневписанный круг ^[24] треугольник представляет собой окружность , лежащая вне треугольника, касательная к одной из его сторон и касательной к продолжениям двух другихов . В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника. ^[3]

Центр вневписанной окружности - это пересечение внутренней биссектрисы одного угла (например, в вершине ) и внешних биссектрис двух других. Центр этого вневписанное называется эксцентрик относительно вершины , или эксцентриком из . ^[3] Поскольку внутренняя биссектриса угла перпендикулярна его внешней биссектрисе, из этого следует, что центр вписанной окружности вместе с тремя центрами вневписанной окружности образуют ортоцентрическую систему . ^{[5] : 182}${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$

Трехлинейные координаты эксцентров [ править ]

В то время как вписанные в имеют трилинейные координаты , эксцентрики имеют trilinears , и . ^{[ необходима цитата ]}${\displaystyle \triangle ABC}$ ${\displaystyle 1:1:1}$${\displaystyle -1:1:1}$${\displaystyle 1:-1:1}$${\displaystyle 1:1:-1}$

Exradii [ править ]

Радиусы вневписанных окружностей называются эксрадиусами .

Экстрадиус вневписанной окружности напротив (так касаясь , с центром в ) равен ^{[25] [26]}${\displaystyle A}$${\displaystyle BC}$${\displaystyle J_{A}}$

${\displaystyle r_{a}={\frac {rs}{s-a}}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}},}$ где ${\displaystyle s={\tfrac {1}{2}}(a+b+c).}$

См . Формулу Герона .

Вывод формулы exradii ^[27] [ править ]

Другие свойства [ править ]

Из приведенных выше формул видно, что вневписанная окружность всегда больше, чем вписанная, и что наибольшая вневписанная окружность касается самой длинной стороны, а наименьшая вневписанная окружность касается самой короткой стороны. Далее, объединение этих формул дает: ^[28]

${\displaystyle \Delta ={\sqrt {rr_{a}r_{b}r_{c}}}.}$

Другие свойства вневписанной окружности [ править ]

Круглая оболочка вневписанных окружностей внутренне касается каждой из вневписанных окружностей и, таким образом, является окружностью Аполлония . ^[29] Радиус этой окружности Аполлония находится где радиус вписанной и является -полупериметр треугольника. ^[30]${\displaystyle {\tfrac {r^{2}+s^{2}}{4r}}}$${\displaystyle r}$${\displaystyle s}$

Имеет место следующих соотношений между inradius , в описанной окружности , -полупериметр и вневписанные радиусами , , : ^[13]${\displaystyle r}$${\displaystyle R}$${\displaystyle s}$${\displaystyle r_{a}}$${\displaystyle r_{b}}$${\displaystyle r_{c}}$

${\displaystyle {\begin{aligned}r_{a}+r_{b}+r_{c}&=4R+r,\\r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}&=s^{2},\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}&=\left(4R+r\right)^{2}-2s^{2}.\end{aligned}}}$

Окружность, проходящая через центры трех вневписанных окружностей, имеет радиус . ^[13]${\displaystyle 2R}$

Если это ортоцентр из , то ^[13]${\displaystyle H}$${\displaystyle \triangle ABC}$

${\displaystyle {\begin{aligned}r_{a}+r_{b}+r_{c}+r&=AH+BH+CH+2R,\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}&=AH^{2}+BH^{2}+CH^{2}+(2R)^{2}.\end{aligned}}}$

Треугольник Нагеля и точка Нагеля [ править ]

В   нажмите треугольник ( ) и${\displaystyle \triangle T_{A}T_{B}T_{C}}$  Точка Нагеля ( )${\displaystyle N}$  треугольник ( ). Оранжевые кружки - это вневписанные окружности треугольника.${\displaystyle \triangle ABC}$

Nagel треугольник или extouch треугольник из обозначаются через вершину , и что эти три точек , где вневписанные окружности коснуться ссылками и где находятся противоположное , и т.д. Это также известно как extouch треугольника из . Окружность из extouch называется круг Mandart . ^{[ необходима цитата ]}${\displaystyle \triangle ABC}$${\displaystyle T_{A}}$${\displaystyle T_{B}}$${\displaystyle T_{C}}$${\displaystyle \triangle ABC}$${\displaystyle T_{A}}$${\displaystyle A}$${\displaystyle \triangle T_{A}T_{B}T_{C}}$${\displaystyle \triangle ABC}$${\displaystyle \triangle T_{A}T_{B}T_{C}}$

Три линии , и называются разветвители треугольника; каждая из них делит пополам периметр треугольника, ^{[ цитата необходима ]}${\displaystyle AT_{A}}$${\displaystyle BT_{B}}$${\displaystyle CT_{C}}$

${\displaystyle AB+BT_{A}=AC+CT_{A}={\frac {1}{2}}\left(AB+BC+AC\right).}$

Разделители пересекаются в одной точке, в точке Нагеля треугольника (или в центре треугольника X ₈ ).${\displaystyle N_{a}}$

Трилинейные координаты для вершин треугольника вне касания задаются ^{[ ссылка ]}

• ${\displaystyle {\text{vertex}}\,T_{A}=0:\csc ^{2}\left({\frac {B}{2}}\right):\csc ^{2}\left({\frac {C}{2}}\right)}$
• ${\displaystyle {\text{vertex}}\,T_{B}=\csc ^{2}\left({\frac {A}{2}}\right):0:\csc ^{2}\left({\frac {C}{2}}\right)}$
• ${\displaystyle {\text{vertex}}\,T_{C}=\csc ^{2}\left({\frac {A}{2}}\right):\csc ^{2}\left({\frac {B}{2}}\right):0.}$

Трилинейные координаты точки Нагеля даются ^{[ ссылка ]}

${\displaystyle \csc ^{2}\left({\frac {A}{2}}\right):\csc ^{2}\left({\frac {B}{2}}\right):\csc ^{2}\left({\frac {C}{2}}\right),}$

или, что то же самое, по закону синуса ,

${\displaystyle {\frac {b+c-a}{a}}:{\frac {c+a-b}{b}}:{\frac {a+b-c}{c}}.}$

Точка Нагеля изотомно сопряжена с точкой Жергонна. ^{[ необходима цитата ]}

Связанные конструкции [ править ]

Девятиконечная окружность и точка Фейербаха [ править ]

В геометрии круг из девяти точек - это круг, который можно построить для любого заданного треугольника . Он назван так потому, что проходит через девять важных точек пересечения, определяемых треугольником. Вот эти девять пунктов : ^{[31] [32]}

• Середина каждой стороны треугольника
• Лапка каждой высоты
• Середина отрезка от каждой вершины треугольника до ортоцентра (где встречаются три высоты; эти отрезки лежат на соответствующих высотах).

В 1822 году Карл Фейербах обнаружил, что окружность любого треугольника с девятью точками касается снаружи трех вневписанных окружностей этого треугольника и внутренне касается его вписанной окружности ; этот результат известен как теорема Фейербаха . Он доказал, что: ^{[ необходима цитата ]}

... окружность, проходящая через основание высот треугольника, касается всех четырех окружностей, которые, в свою очередь, касаются трех сторон треугольника ... ( Фейербах 1822 ) harv error: no target: CITEREFFeuerbach1822 (help)

Центр треугольника, в котором соприкасаются вписанная окружность и окружность из девяти точек, называется точкой Фейербаха .

Внутренний и эксцентральный треугольники [ править ]

Точки пересечения внутреннего угла биссектрис с сегментами , , и являются вершинами incentral треугольника . Трилинейные координаты вершин внутреннего треугольника задаются формулой ^{[ необходимая цитата ]}${\displaystyle \triangle ABC}$${\displaystyle BC}$${\displaystyle CA}$${\displaystyle AB}$

• ${\displaystyle \ \left({\text{vertex opposite}}\,A\right)=0:1:1}$
• ${\displaystyle \ \left({\text{vertex opposite}}\,B\right)=1:0:1}$
• ${\displaystyle \ \left({\text{vertex opposite}}\,C\right)=1:1:0.}$

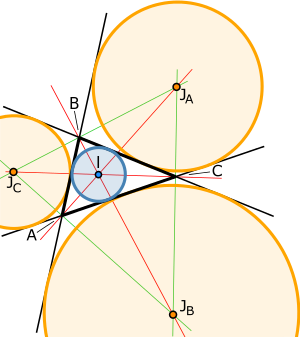
Excentral треугольник опорного треугольника имеет вершины в центрах Вневписанных эталонного треугольника. Его стороны на внешний угол биссектрис опорного треугольника (смотри рисунок в верхней части страницы ). Трилинейные координаты вершин эксцентрального треугольника задаются формулой ^{[ необходима цитата ]}

• ${\displaystyle ({\text{vertex opposite}}\,A)=-1:1:1}$
• ${\displaystyle ({\text{vertex opposite}}\,B)=1:-1:1}$
• ${\displaystyle ({\text{vertex opposite}}\,C)=1:1:-1.}$

Уравнения для четырех кругов [ править ]

Пусть будет переменная точка в координатах трилинейных , и пусть , , . Четыре описанных выше кружка эквивалентны любому из двух приведенных уравнений: ^{[33] : 210–215}${\displaystyle x:y:z}$${\displaystyle u=\cos ^{2}\left(A/2\right)}$${\displaystyle v=\cos ^{2}\left(B/2\right)}$${\displaystyle w=\cos ^{2}\left(C/2\right)}$

• Вокруг:

  ${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy&=0\\\pm {\sqrt {x}}\cos \left({\frac {A}{2}}\right)\pm {\sqrt {y}}\cos \left({\frac {B}{2}}\right)\pm {\sqrt {z}}\cos \left({\frac {C}{2}}\right)&=0\end{aligned}}}$

• ${\displaystyle A}$- вневписанный круг:

  ${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy&=0\\\pm {\sqrt {-x}}\cos \left({\frac {A}{2}}\right)\pm {\sqrt {y}}\cos \left({\frac {B}{2}}\right)\pm {\sqrt {z}}\cos \left({\frac {C}{2}}\right)&=0\end{aligned}}}$

• ${\displaystyle B}$- вневписанный круг:

  ${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy&=0\\\pm {\sqrt {x}}\cos \left({\frac {A}{2}}\right)\pm {\sqrt {-y}}\cos \left({\frac {B}{2}}\right)\pm {\sqrt {z}}\cos \left({\frac {C}{2}}\right)&=0\end{aligned}}}$

• ${\displaystyle C}$- вневписанный круг:

  ${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy&=0\\\pm {\sqrt {x}}\cos \left({\frac {A}{2}}\right)\pm {\sqrt {y}}\cos \left({\frac {B}{2}}\right)\pm {\sqrt {-z}}\cos \left({\frac {C}{2}}\right)&=0\end{aligned}}}$

Теорема Эйлера [ править ]

Теорема Эйлера утверждает, что в треугольнике:

${\displaystyle (R-r)^{2}=d^{2}+r^{2},}$

где и - радиус описанной окружности и внутренний радиус, соответственно, и - расстояние между центром описанной окружности и центром.${\displaystyle R}$${\displaystyle r}$${\displaystyle d}$

Для вневписанных кругов уравнение аналогично:

${\displaystyle \left(R+r_{\text{ex}}\right)^{2}=d_{\text{ex}}^{2}+r_{\text{ex}}^{2},}$

где - радиус одной из вневписанных окружностей, а - расстояние между центром описанной окружности и центром этой вневписанной окружности. ^{[34] [35] [36]}${\displaystyle r_{\text{ex}}}$${\displaystyle d_{\text{ex}}}$

Обобщение на другие полигоны [ править ]

Некоторые (но не все) четырехугольники имеют вписанную окружность. Эти четырехугольники называются касательными . Среди множества их свойств, пожалуй, наиболее важным является то, что две пары противоположных сторон имеют равные суммы. Это называется теоремой Пито . ^{[ необходима цитата ]}

В более общем смысле, многоугольник с любым количеством сторон, который имеет вписанную окружность (то есть ту, которая касается каждой стороны), называется касательным многоугольником . ^{[ необходима цитата ]}

См. Также [ править ]

• Circumgon
• Описанный круг  - круг, проходящий через все вершины многоугольника.
• Экс касательный четырехугольник
• Теорема Харкорта  - Площадь треугольника от его сторон и расстояния от вершин до любой прямой, касающейся его вписанной окружности.
• Circumconic и inconic  - коническое сечение, которое проходит через вершины треугольника или касается его сторон.
• Вписанная сфера
• Сила точки
• Штайнер инеллипс
• Тангенциальный четырехугольник
• Теорема триллия  - утверждение о свойствах вписанных и описанных кругов

Заметки [ править ]

Ссылки [ править ]

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в современную геометрию треугольника и круга (2-е изд.), Нью-Йорк: Barnes & Noble , LCCN  52013504
• Кей, Дэвид К. (1969), Геометрия колледжа , Нью-Йорк: Холт, Райнхарт и Уинстон , LCCN  69012075
• Кимберлинг, Кларк (1998). «Центры треугольников и центральные треугольники». Congressus Numerantium (129): i – xxv, 1–295.
• Поцелуй, Шандор (2006). "Ортопедические и интуитивно понятные треугольники". Форум Geometricorum (6): 171–177.

Внешние ссылки [ править ]

• Вывод формулы для радиуса вписанной окружности треугольника
• Вайсштейн, Эрик В. «Окружение» . MathWorld .

Интерактивный [ править ]

• Треугольник, вписанный в    окружность, окружность   правильного многоугольника    С интерактивной анимацией
• Построение центра / вписанной окружности треугольника с помощью циркуля и линейки Интерактивная анимированная демонстрация
• Теорема о равных вписанных окружностях при разрубании узла
• Теорема о пяти вписанных окружностях при разрубании узла
• Пары вписанных окружностей в четырехугольник в разрубленном узле
• Интерактивный Java-апплет для Incenter