Линейная функция (исчисление)

В этой статье отсутствует информация о случае функций многих переменных и векторных функций, которые необходимо учитывать, поскольку эта статья связана с матрицей Якоби . Разверните статью, чтобы включить эту информацию. Более подробная информация может быть на странице обсуждения . ( Февраль 2020 г. )

График линейной функции: ${\ Displaystyle у (х) = - х + 2}$

В исчислении и смежных областях математики линейная функция от действительных чисел к действительным числам - это функция, график которой (в декартовых координатах ) представляет собой линию на плоскости. ^[1] Характерным свойством линейных функций является то, что при изменении входной переменной изменение на выходе пропорционально изменению на входе.

Линейные функции связаны с линейными уравнениями .

Свойства [ править ]

Линейная функция - это полиномиальная функция, в которой переменная x имеет степень не выше единицы: ^[2]

${\ displaystyle f (x) = ax + b}$.

Такая функция называется линейной, потому что ее график , набор всех точек на декартовой плоскости , представляет собой линию . Коэффициент a называется наклоном функции и прямой (см. Ниже).${\ Displaystyle (х, е (х))}$

Если наклон равен , это постоянная функция, определяющая горизонтальную линию, которую некоторые авторы исключают из класса линейных функций. ^[3] При таком определении степень линейного многочлена будет ровно одна, а его график будет прямой, которая не является ни вертикальной, ни горизонтальной. Однако в этой статье это обязательное условие, поэтому постоянные функции будут считаться линейными.${\ displaystyle a = 0}$ ${\ displaystyle f (x) = b}$${\ displaystyle a \ neq 0}$

Если тогда линейная функция называется однородной . Такая функция определяет линию, проходящую через начало системы координат, то есть точку . В текстах по продвинутой математике термин линейная функция часто обозначает специфически однородные линейные функции, а термин аффинная функция используется для общего случая, который включает .${\ displaystyle b = 0}$${\ Displaystyle (х, у) = (0,0)}$${\ displaystyle b \ neq 0}$

Естественный домен линейной функции , набор допустимых входных значений для х , это все множества действительных чисел , можно также рассматривать такие функции , с й в произвольном поле , принимая коэффициенты A, B в этой области. ${\ displaystyle f (x)}$${\ Displaystyle х \ in \ mathbb {R}.}$

График не является вертикальной линией , имеющей ровно один пересечением с у -Axis, его у -intercept точки у -intercept значения также называется начальное значением из Если граф не является горизонтальной линией , имеющей ровно один пересечения с х оси х, то х -intercept точка X -intercept значение решение уравнения также называется корень или ноль из${\ displaystyle y = f (x) = ax + b}$${\ displaystyle (x, y) = (0, b).}$${\ displaystyle y = f (0) = b}$${\ displaystyle f (x).}$${\ displaystyle a \ neq 0,}$${\ displaystyle (x, y) = (- {\ tfrac {b} {a}}, 0).}$${\ displaystyle x = - {\ tfrac {b} {a}},}$${\ displaystyle f (x) = 0,}$${\ displaystyle f (x).}$

Наклон [ править ]

Наклон линии представляет собой отношение между изменением х , обозначается , и соответствующее изменение у , обозначается${\ Displaystyle {\ tfrac {\ Delta y} {\ Delta x}}}$${\ displaystyle \ Delta x}$${\ displaystyle \ Delta y}$

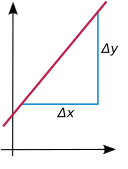
Наклон от невертикальной линии представляет собой число, меры , как круто наклонена линия (подъем заскоки). Если линия является графиком линейной функции , этот наклон задается константой a . ${\ displaystyle f (x) = ax + b}$

Данные наклона измеряет постоянную скорость изменения на единицу изменения в х : всякий раз , когда входной сигнал х увеличивается на единицу, выход изменяется на течение единицы: и в более общем случае для любого числа . Если наклон положительный , то функция возрастает; если , то убывает${\ displaystyle f (x)}$${\ Displaystyle е (х {+} 1) = е (х) + а}$${\displaystyle f(x{+}\Delta x)=f(x)+a\Delta x}$${\displaystyle \Delta x}$${\displaystyle a>0}$${\displaystyle f(x)}$${\displaystyle a<0}$${\displaystyle f(x)}$

В исчислении производная общей функции измеряет скорость ее изменения. Линейная функция имеет постоянную скорость изменения, равную ее наклону a , поэтому ее производная является постоянной функцией . ${\displaystyle f(x)=ax+b}$${\displaystyle f\,'(x)=a}$

Фундаментальная идея дифференциального исчисления состоит в том, что любая гладкая функция (не обязательно линейная) может быть приближена близко к заданной точке единственной линейной функцией. Производное представляет собой наклон этой линейной функции, а приближение: для . График линейной аппроксимации - это касательная линия графика в точке . Наклон производной обычно меняется в зависимости от точки c . Линейные функции можно охарактеризовать как единственные действительные функции, производная которых постоянна: если для всех x , то для .${\displaystyle f(x)}$${\displaystyle x=c}$ ${\displaystyle f\,'(c)}$${\displaystyle f(x)\approx f\,'(c)(x{-}c)+f(c)}$${\displaystyle x\approx c}$${\displaystyle y=f(x)}$${\displaystyle (c,f(c))}$${\displaystyle f\,'(c)}$${\displaystyle f\,'(x)=a}$${\displaystyle f(x)=ax+b}$${\displaystyle b=f(0)}$

Склон-пересечение, точка-наклон и двухточечная форма [ править ]

Данная линейная функция может быть записана в виде нескольких стандартных формул, отображающих ее различные свойства. Самая простая - это форма с пересечением наклона : ${\displaystyle f(x)}$

${\displaystyle f(x)=ax+b}$,

из которого можно сразу увидеть наклон a и начальное значение , которое является пересечением оси y графика . ${\displaystyle f(0)=b}$${\displaystyle y=f(x)}$

Учитывая наклон a и одно известное значение , мы записываем форму точки наклона : ${\displaystyle f(x_{0})=y_{0}}$

${\displaystyle f(x)=a(x{-}x_{0})+y_{0}}$.

Графически это дает линию с наклоном а, проходящую через точку . ${\displaystyle y=f(x)}$${\displaystyle (x_{0},y_{0})}$

Образуют две точки начинается с двух известных значений и . Один вычисляет уклон и вставляет его в форму точечного уклона: ${\displaystyle f(x_{0})=y_{0}}$${\displaystyle f(x_{1})=y_{1}}$${\displaystyle a={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}}$

${\displaystyle f(x)={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x{-}x_{0}\!)+y_{0}}$.

Его график представляет собой единственную прямую, проходящую через точки . Уравнение также может быть записано, чтобы подчеркнуть постоянный наклон:${\displaystyle y=f(x)}$${\displaystyle (x_{0},y_{0}\!),(x_{1},y_{1}\!)}$${\displaystyle y=f(x)}$

${\displaystyle {\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}}$.

Связь с линейными уравнениями [ править ]

Линейные функции обычно возникают из практических задач, связанных с переменными с линейной зависимостью, то есть подчиняющимися линейному уравнению . Если можно решить это уравнение относительно y , получив${\displaystyle x,y}$ ${\displaystyle Ax+By=C}$${\displaystyle B\neq 0}$

${\displaystyle y=-{\tfrac {A}{B}}x+{\tfrac {C}{B}}=ax+b,}$

где обозначены и . То есть, можно считать , у в качестве зависимого переменного (выхода) , полученных от независимого переменного (входа) х через линейную функцию: . В координатной плоскости xy возможные значения образуют линию, график функции . Если в исходном уравнении результирующая линия является вертикальной и не может быть записана как .${\displaystyle a=-{\tfrac {A}{B}}}$${\displaystyle b={\tfrac {C}{B}}}$${\displaystyle y=f(x)=ax+b}$${\displaystyle (x,y)}$${\displaystyle f(x)}$${\displaystyle B=0}$${\displaystyle x={\tfrac {C}{A}}}$${\displaystyle y=f(x)}$

Особенности графика можно интерпретировать в терминах переменных x и y . У -intercept является начальным значением в . Наклон а измеряет скорость изменения выхода y на единицу изменения входа x . На графике, перемещая одну единицу вправо (увеличение х на 1) перемещает у -value вверх : то есть . Отрицательный наклон a указывает на уменьшение y для каждого увеличения x .${\displaystyle y=f(x)=ax+b}$${\displaystyle y=f(0)=b}$${\displaystyle x=0}$${\displaystyle f(x{+}1)=f(x)+a}$

Например, линейная функция имеет наклон , точку пересечения y и точку пересечения x .${\displaystyle y=-2x+4}$${\displaystyle a=-2}$${\displaystyle (0,b)=(0,4)}$${\displaystyle (2,0)}$

Пример [ править ]

Предположим, салями и колбаса стоят 6 и 3 евро за килограмм, а мы хотим купить на 12 евро. Сколько каждого из них мы можем купить? Если x килограммов салями и y килограммов колбасы стоит в сумме 12 евро, то 6 x x + 3 x y = 12 евро. Решение для y дает форму точки наклона , как указано выше. То есть, если мы сначала выберем количество салями x , количество колбасы можно будет вычислить как функцию . Поскольку салями стоит вдвое дороже, чем колбаса, добавление одного килограмма салями уменьшает колбасу на 2 килограмма:, и наклон составляет −2. Точка пересечения y соответствует покупке всего 4 кг колбасы; в то время как х${\displaystyle y=-2x+4}$${\displaystyle y=f(x)=-2x+4}$${\displaystyle f(x{+}1)=f(x)-2}$${\displaystyle (x,y)=(0,4)}$-точка перехвата соответствует покупке всего 2 кг салями. ${\displaystyle (x,y)=(2,0)}$

Обратите внимание, что на графике есть точки с отрицательными значениями x или y , которые не имеют значения с точки зрения исходных переменных (если только мы не представляем себе продажу мяса мяснику). Таким образом, мы должны ограничить нашу функцию доменом . ${\displaystyle f(x)}$${\displaystyle 0\leq x\leq 2}$

Кроме того, мы могли бы выбрать y в качестве независимой переменной и вычислить x с помощью обратной линейной функции: по области .${\displaystyle x=g(y)=-{\tfrac {1}{2}}y+2}$${\displaystyle 0\leq y\leq 4}$

Связь с другими классами функций [ править ]

Если коэффициент переменной не равен нулю ( a 0 ), то линейная функция представлена полиномом 1 степени (также называемым линейным полиномом ), в противном случае это постоянная функция - также полиномиальная функция, но нулевой степени. .

Прямая линия, нарисованная в другой системе координат, может представлять другие функции.

Например, он может представлять экспоненциальную функцию, когда ее значения выражены в логарифмической шкале . Это означает, что когда log ( g ( x )) является линейной функцией от x , функция g является экспоненциальной. В линейных функциях увеличение ввода на одну единицу приводит к увеличению вывода на фиксированную величину, которая представляет собой наклон графика функции. В случае экспоненциальных функций увеличение ввода на одну единицу приводит к увеличению вывода на фиксированное кратное число, которое известно как основание экспоненциальной функции.

Если и аргументы, и значения функции находятся в логарифмической шкале (т. Е. Когда log ( y ) является линейной функцией log ( x ) ), тогда прямая линия представляет собой степенной закон :

${\displaystyle \log _{r}y=a\log _{r}x+b\quad \Rightarrow \quad y=r^{b}\cdot x^{a}}$

С другой стороны, график линейной функции в полярных координатах :

${\displaystyle r=f(\theta )=a\theta +b}$

является спиралью Архимеда, если и окружностью в противном случае.${\displaystyle a\neq 0}$

Примечания [ править ]

См. Также [ править ]

• Аффинное отображение , обобщение
• Арифметическая прогрессия , линейная функция от целочисленного аргумента

Ссылки [ править ]

• Джеймс Стюарт (2012), Calculus: Early Transcendentals , edition 7E, Brooks / Cole. ISBN  978-0-538-49790-9
• Своковски, Эрл У. (1983), Исчисление с аналитической геометрией (альтернативный редактор), Бостон: Prindle, Weber & Schmidt, ISBN 0871503417

Внешние ссылки [ править ]

• https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
• http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf