Квадратичная формула

Квадратичная функция с корнями x  = 1 и x  = 4.

В элементарной алгебре , то квадратичная формула представляет собой формулу , которая обеспечивает решение (S) к квадратному уравнению . Существуют и другие способы решения квадратного уравнения вместо использования квадратной формулы, такие как факторизация (прямое разложение, группировка, метод AC ), завершение квадрата , построение графиков и другие. ^[1]

Для общего квадратного уравнения вида

${\ displaystyle ax ^ {2} + bx + c = 0}$

где x представляет неизвестное, a , b и c представляют константы с a ≠ 0 , квадратная формула:

$${\ Displaystyle х = {\ гидроразрыва {-b \ pm {\ sqrt {b ^ {2} -4ac}}} {2a}} \ \}$$

где знак плюс-минус «±» означает, что квадратное уравнение имеет два решения. ^[2] Написанные отдельно, они становятся:

${\ displaystyle x_ {1} = {\ frac {-b + {\ sqrt {b ^ {2} -4ac}}} {2a}} \ quad {\ text {and}} \ quad x_ {2} = {\ гидроразрыв {-b - {\ sqrt {b ^ {2} -4ac}}} {2a}}}$

Каждое из этих двух решений также называется корнем (или нулем) квадратного уравнения. Геометрически эти корни представляют собой значения x, при которых любая парабола , явно заданная как y = ax ² + bx + c , пересекает ось x . ^[3]

Помимо того, что формула дает нули любой параболы, квадратная формула также может использоваться для определения оси симметрии параболы, ^[4] и количества действительных нулей, содержащихся в квадратном уравнении. ^[5]

Эквивалентные формулировки [ править ]

Квадратичная формула также может быть записана как:

${\ displaystyle x = {\ frac {-b} {2a}} \ pm {\ sqrt {\ frac {b ^ {2} -4ac} {4a ^ {2}}}} \ \,}$

который можно упростить до:

${\ displaystyle x = - {\ frac {b} {2a}} \ pm {\ sqrt {\ left ({\ frac {b} {2a}} \ right) ^ {2} - {\ frac {c} { а}}}} \ \.}$

Эта версия формулы удобна, когда используются комплексные корни, и в этом случае выражение вне квадратного корня будет действительной частью, а выражение квадратного корня - мнимой частью. Выражение внутри квадратного корня является дискриминантом. Сложное выражение будет:

${\ displaystyle x = - {\ frac {\ b} {2a}} \ pm i {\ sqrt {{\ Big |} \ left ({\ frac {\ b} {2a}} \ right) ^ {2} - {\ frac {c} {a}} {\ Big |}}} \ \.}$

Метод Мюллера [ править ]

Менее известная квадратичная формула, которая используется в методе Мюллера и которую можно найти из формул Виета , дает те же корни через уравнение:

${\ displaystyle x = {\ frac {-2c} {b \ pm {\ sqrt {b ^ {2} -4ac}}}} = {\ frac {2c} {- b \ mp {\ sqrt {b ^ { 2} -4ac \}}}} \ \.}$

Формулировки на основе альтернативных параметризаций [ править ]

Стандартная параметризация квадратного уравнения:

${\ displaystyle ax ^ {2} + bx + c = 0 \ \.}$

Некоторые источники, особенно старые, используют альтернативные параметризации квадратного уравнения, такие как

${\ displaystyle ax ^ {2} -2b_ {1} x + c = 0}$, где , ^[6]${\displaystyle b_{1}=-b/2}$

или же

${\displaystyle ax^{2}+2b_{2}x+c=0}$, где . ^[7]${\displaystyle b_{2}=b/2}$

Эти альтернативные параметризации приводят к несколько иным формам решения, которые в остальном эквивалентны стандартной параметризации.

Вывод формулы [ править ]

В литературе доступно множество различных методов вывода формулы квадратного уравнения. Стандартный - это простое применение техники завершения квадрата . ^{[8] [9] [10] [11]} Альтернативные методы иногда проще, чем заполнение квадрата, и могут предложить интересное понимание других областей математики.

Используя технику «завершения квадрата» [ править ]

Стандартный метод [ править ]

Разделите квадратное уравнение на , что разрешено, потому что оно не равно нулю:${\displaystyle a}$${\displaystyle a}$

${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\ \ .}$

Вычесть c/а с обеих сторон уравнения, что дает:

${\displaystyle x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}\ \ .}$

Квадратное уравнение теперь имеет форму, к которой применим метод завершения квадрата . Фактически, добавляя константу к обеим сторонам уравнения, так что левая часть становится полным квадратом, квадратное уравнение становится следующим:

${\displaystyle x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2}\ \ ,}$

который производит:

${\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+{\frac {b^{2}}{4a^{2}}}\ \ .}$

Соответственно, переставив члены в правой части так, чтобы они имели общий знаменатель, мы получим:

${\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}\ \ .}$

Таким образом, площадь завершена. Извлечение квадратного корня из обеих частей дает следующее уравнение:

${\displaystyle x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}\ \ .}$

В этом случае, выделение даст квадратную формулу:${\displaystyle x}$

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}\ \ .}$

Есть много альтернатив этого происхождения с небольшими отличиями, в основном касающимися манипуляции с .${\displaystyle a}$

Метод 2 [ править ]

В большинстве текстов по алгебре, опубликованных за последние несколько десятилетий, учат завершать квадрат, используя последовательность, представленную ранее:

1. Разделите каждую сторону на, чтобы получился полином однозначный .${\displaystyle a}$
2. Переставить.
3. Добавьте к обеим сторонам, чтобы завершить квадрат.${\displaystyle \textstyle \left({\frac {b}{2a}}\right)^{2}}$
4. Переставьте члены в правой части, чтобы получить общий знаменатель.
5. Извлеките квадратный корень из обеих частей.
6. Изолировать .${\displaystyle x}$

Завершение квадрата также может быть выполнено с помощью иногда более короткой и простой последовательности: ^[12]

1. Умножьте каждую сторону на ,${\displaystyle 4a}$
2. Переставить.
3. Добавьте к обеим сторонам, чтобы завершить квадрат.${\displaystyle b^{2}}$
4. Извлеките квадратный корень из обеих частей.
5. Изолировать .${\displaystyle x}$

В этом случае формулу корней квадратного уравнения можно вывести следующим образом:

${\displaystyle {\begin{aligned}ax^{2}+bx+c&=0\\4a^{2}x^{2}+4abx+4ac&=0\\4a^{2}x^{2}+4abx&=-4ac\\4a^{2}x^{2}+4abx+b^{2}&=b^{2}-4ac\\(2ax+b)^{2}&=b^{2}-4ac\\2ax+b&=\pm {\sqrt {b^{2}-4ac}}\\2ax&=-b\pm {\sqrt {b^{2}-4ac}}\\x&={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .\end{aligned}}}$

Этот вывод квадратной формулы является древним и был известен в Индии, по крайней мере, еще в 1025 году. ^[13] По сравнению с выводом в стандартном использовании, этот альтернативный вывод избегает дробей и квадратичных дробей до последнего шага и, следовательно, не требует перестановка после шага 3, чтобы получить общий знаменатель в правой части. ^[12]

Метод 3 [ править ]

Подобно методу 1, разделите каждую сторону на, чтобы левый полином стал моническим (т. Е. Коэффициент при становится 1 ).${\displaystyle a}$${\displaystyle x^{2}}$

${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\ \ .}$

Напишите уравнение в более компактном и удобном для понимания формате:

${\displaystyle x^{2}+Bx+C=0}$

где и .${\displaystyle \textstyle B={\frac {b}{a}}}$${\displaystyle \textstyle C={\frac {c}{a}}}$

Завершите квадрат, добавив к первым двум членам и вычтя его из третьего члена:${\displaystyle \textstyle {\frac {B^{2}}{4}}}$

${\displaystyle \left(x+{\frac {B}{2}}\right)^{2}+\left(C-{\frac {B^{2}}{4}}\right)=0}$

Переставьте левую сторону в два квадрата :

${\displaystyle \left(x+{\frac {B}{2}}\right)^{2}-\left({\sqrt {{\frac {B^{2}}{4}}-C}}\right)^{2}=0}$

и фактор это:

${\displaystyle \left(x+{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}\right)\left(x+{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}\right)=0}$

откуда следует, что либо

${\displaystyle x+{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}=0}$

или же

${\displaystyle x+{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}=0}$

Каждое из этих двух уравнений линейно и может быть решено относительно , получив:${\displaystyle x}$

${\displaystyle x=-{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}}$ или же ${\displaystyle x=-{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}}$

Путем повторного выражения и обратно в и , соответственно, можно получить квадратную формулу. ^{[ необходима цитата ]}${\displaystyle B}$${\displaystyle C}$${\displaystyle \textstyle {\frac {b}{a}}}$${\displaystyle \textstyle {\frac {c}{a}}}$

Путем подстановки [ править ]

Другой прием - решение заменой . ^[14] В этом методе мы подставляем квадратичный, чтобы получить:${\displaystyle x=y+m}$

${\displaystyle a(y+m)^{2}+b(y+m)+c=0\ \ .}$

Расширяя результат, а затем собирая мощности, получаем:${\displaystyle y}$

${\displaystyle ay^{2}+y(2am+b)+\left(am^{2}+bm+c\right)=0\ \ .}$

Мы еще не наложили второе условие на и , поэтому теперь выбираем так, чтобы средний член исчезал. То есть или . Вычитая постоянный член из обеих частей уравнения (чтобы переместить его в правую часть), а затем делить на, получаем:${\displaystyle y}$${\displaystyle m}$${\displaystyle m}$${\displaystyle 2am+b=0}$${\displaystyle \textstyle m={\frac {-b}{2a}}}$${\displaystyle a}$

${\displaystyle y^{2}={\frac {-\left(am^{2}+bm+c\right)}{a}}\ \ .}$

Замена дает:${\displaystyle m}$

${\displaystyle y^{2}={\frac {-\left({\frac {b^{2}}{4a}}+{\frac {-b^{2}}{2a}}+c\right)}{a}}={\frac {b^{2}-4ac}{4a^{2}}}\ \ .}$

Следовательно,

${\displaystyle y=\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}}$

Путем повторного выражения в терминах использования формулы можно получить обычную квадратную формулу:${\displaystyle y}$${\displaystyle x}$${\displaystyle \textstyle x=y+m=y-{\frac {b}{2a}}}$

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .}$

Используя алгебраические тождества [ править ]

Следующий метод использовался многими историческими математиками: ^[15]

Пусть корни стандартного квадратного уравнения равны r ₁ и r ₂ . Вывод начинается с напоминания об идентичности:

${\displaystyle (r_{1}-r_{2})^{2}=(r_{1}+r_{2})^{2}-4r_{1}r_{2}\ \ .}$

Взяв квадратный корень с обеих сторон, получим:

${\displaystyle r_{1}-r_{2}=\pm {\sqrt {(r_{1}+r_{2})^{2}-4r_{1}r_{2}}}\ \ .}$

Поскольку коэффициент a 0 , мы можем разделить стандартное уравнение на a, чтобы получить квадратный многочлен с теми же корнями. А именно,

${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=(x-r_{1})(x-r_{2})=x^{2}-(r_{1}+r_{2})x+r_{1}r_{2}\ \ .}$

Из этого мы можем видеть, что сумма корней стандартного квадратного уравнения определяется как -б/а, а произведение этих корней равно c/а. Следовательно, тождество можно переписать как:

${\displaystyle r_{1}-r_{2}=\pm {\sqrt {\left(-{\frac {b}{a}}\right)^{2}-4{\frac {c}{a}}}}=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}-{\frac {4ac}{a^{2}}}}}=\pm {\frac {\sqrt {b^{2}-4ac}}{a}}\ \ .}$

Сейчас же,

${\displaystyle r_{1}={\frac {(r_{1}+r_{2})+(r_{1}-r_{2})}{2}}={\frac {-{\frac {b}{a}}\pm {\frac {\sqrt {b^{2}-4ac}}{a}}}{2}}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .}$

Поскольку r ₂ = - r ₁ -б/а, если взять

${\displaystyle r_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$

тогда получаем

${\displaystyle r_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\ \ ;}$

и если мы вместо этого возьмем

${\displaystyle r_{1}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}$

затем мы вычисляем, что

${\displaystyle r_{2}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\ \ .}$

Комбинируя эти результаты с использованием стандартного сокращения ±, мы получаем, что решения квадратного уравнения имеют вид:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .}$

Резольвенты Лагранжа [ править ]

Альтернативный способ получения квадратичной формулы осуществляется с помощью метода Лагранжа резольвент , ^[16] , которая является частью ранней теории Галуа . ^[17] Этот метод может быть обобщен, чтобы получить корни кубических многочленов и многочленов четвертой степени , и приводит к теории Галуа, которая позволяет понять решение алгебраических уравнений любой степени в терминах группы симметрии их корней, теории Галуа группа .

Этот подход больше фокусируется на корнях, чем на преобразовании исходного уравнения. Для монического квадратичного многочлена

${\displaystyle x^{2}+px+q\ \ ,}$

предположить, что это фактор как

${\displaystyle x^{2}+px+q=(x-\alpha )(x-\beta )\ \ ,}$

Увеличение урожайности

${\displaystyle x^{2}+px+q=x^{2}-(\alpha +\beta )x+\alpha \beta \ \ ,}$

где p = - ( α + β ) и q = αβ .

Так как порядок умножения не имеет значения, можно переключить α и β , и значения р и д не изменится: можно сказать , что р и д являются симметричные полиномы в & alpha ; и & beta . Фактически, это элементарные симметричные многочлены - любой симметричный многочлен от α и β может быть выражен через α + β и αβ.Подход теории Галуа к анализу и решению многочленов таков: с учетом коэффициентов многочлена, которые являются симметричными функциями от корней, можно ли «нарушить симметрию» и восстановить корни? Таким образом, решение полинома степени n связано со способами перестановки (« перестановки ») n терминов, которая называется симметричной группой из n букв и обозначается S _n . Для квадратичного многочлена единственный способ переставить два члена - это поменять их местами (« транспонировать »), и, таким образом, решение квадратного многочлена просто.

Чтобы найти корни α и β , рассмотрим их сумму и разность:

${\displaystyle {\begin{aligned}r_{1}&=\alpha +\beta \\r_{2}&=\alpha -\beta \ \ .\end{aligned}}}$

Они называются резольвентами Лагранжа многочлена; обратите внимание, что один из них зависит от порядка корней, что является ключевым моментом. Можно восстановить корни из резольвент, обращая приведенные выше уравнения:

${\displaystyle {\begin{aligned}\alpha &=\textstyle {\frac {1}{2}}\left(r_{1}+r_{2}\right)\\\beta &=\textstyle {\frac {1}{2}}\left(r_{1}-r_{2}\right)\ \ .\end{aligned}}}$

Таким образом, решение для резольвент дает исходные корни.

Теперь r ₁ = α + β является симметричной функцией от α и β , поэтому ее можно выразить через p и q , и на самом деле r ₁ = - p, как отмечалось выше. Но r ₂ = α - β несимметрично, поскольку переключение α и β дает - r ₂ = β - α (формально это называется групповым действием симметрической группы корней). Поскольку r₂ не является симметричным, его нельзя выразить через коэффициенты p и q , поскольку они симметричны по корням и, следовательно, любое полиномиальное выражение, включающее их. Изменение порядка корней изменяет r ₂ только в -1 раз, и, таким образом, квадрат r ₂ ² = ( α - β ) ² симметричен по корням и, таким образом, выражается через p и q . Используя уравнение

${\displaystyle (\alpha -\beta )^{2}=(\alpha +\beta )^{2}-4\alpha \beta \ \ }$

дает

${\displaystyle r_{2}^{2}=p^{2}-4q\ \ }$

и поэтому

${\displaystyle r_{2}=\pm {\sqrt {p^{2}-4q}}\ \ }$

Если взять положительный корень, нарушив симметрию, получится:

${\displaystyle {\begin{aligned}r_{1}&=-p\\r_{2}&={\sqrt {p^{2}-4q}}\end{aligned}}}$

и поэтому

${\displaystyle {\begin{aligned}\alpha &={\tfrac {1}{2}}\left(-p+{\sqrt {p^{2}-4q}}\right)\\\beta &={\tfrac {1}{2}}\left(-p-{\sqrt {p^{2}-4q}}\right)\ \ .\end{aligned}}}$

Таким образом, корни

${\displaystyle \textstyle {\frac {1}{2}}\left(-p\pm {\sqrt {p^{2}-4q}}\right)}$

что является квадратичной формулой. Подставив p =б/а, q =c/адает обычную форму для случая, когда квадратичная не является монической. Противовоспалительные средства можно распознать какr ₁/2 знак равно - п/2 знак равно - б/2 а- вершина, а r ₂ ² = p ² - 4 q - дискриминант (монического многочлена).

Аналогичный, но более сложный метод работает для кубических уравнений , в которых есть три резольвенты и квадратное уравнение («разрешающий многочлен»), связывающее r ₂ и r ₃ , которое можно решить с помощью квадратного уравнения, и аналогично для уравнения четвертой степени ( степени 4), разрешающий многочлен которой является кубикой, которая, в свою очередь, может быть решена. ^[16] Тот же метод для уравнения пятой степени дает полином степени 24, что не упрощает задачу, и, фактически, решения уравнений пятой степени в целом не могут быть выражены с использованием только корней.

Историческое развитие [ править ]

Самые ранние методы решения квадратных уравнений были геометрическими. Вавилонские клинописные таблички содержат задачи, сводимые к решению квадратных уравнений. ^[18] Египетский Берлинский папирус , восходящий к Среднему царству (2050 г. до н.э. - 1650 г. до н.э.), содержит решение двухчленного квадратного уравнения. ^[19]

Греческий математик Евклид (около 300 г. до н.э.) использовал геометрические методы для решения квадратных уравнений в Книге 2 своих Элементов , влиятельном математическом трактате. ^[20] Правила квадратных уравнений появляются в китайской книге «Девять глав по математическому искусству» около 200 г. до н.э. ^{[21] [22]} В своей работе « Арифметика» греческий математик Диофант (около 250 г. н.э.) решил квадратные уравнения методом более узнаваемым алгебраическим, чем геометрическая алгебра Евклида. ^[20] Его решение дает только один корень, даже если оба корня положительны. ^[23]

Индийский математик Брахмагупта (597–668 гг. Н.э.) подробно описал квадратичную формулу в своем трактате Brāhmasphuṭasiddhānta, опубликованном в 628 г. ^[24], но написанном словами вместо символов. ^[25] Его решение квадратного уравнения ax ² + bx = c было следующим: «К абсолютному числу, умноженному в четыре раза на квадрат [коэффициент], добавьте квадрат [коэффициент при] среднего члена; квадратный корень из того же, за вычетом [коэффициента] среднего члена, деленный на удвоенное значение [коэффициента] квадрата ». ^[26] Это эквивалентно:

${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}\ \ .}$

Персидский математик IX века Мухаммад ибн Муса аль-Харизми решал квадратные уравнения алгебраически. ^[27] Квадратичная формула, охватывающая все случаи, была впервые получена Симоном Стевином в 1594 году. ^[28] В 1637 году Рене Декарт опубликовал «Геометрию», содержащую частные случаи квадратичной формулы в той форме, которую мы знаем сегодня. ^[29]

Существенное использование [ править ]

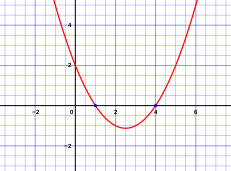
Геометрическое значение [ править ]

В терминах координатной геометрии парабола - это кривая, ( x , y ) -координаты которой описываются полиномом второй степени, то есть любым уравнением вида:

${\displaystyle y=p(x)=a_{2}x^{2}+a_{1}x+a_{0}\ \ ,}$

где р представляет собой многочлен степени 2 и с ₀ , ₁ , и ₂ ≠ 0 постоянные коэффициенты , чьи индексы соответствуют степени их соответствующих термина. Геометрическая интерпретация квадратной формулы состоит в том, что она определяет точки на оси x, в которых парабола пересекает ось. Кроме того, если бы квадратная формула рассматривалась как два члена,

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}}$

ось симметрии появляется как линии х = -б/2 а. Другой термин,√ b ² - 4 ac/2 а, показывает расстояние, на котором нули находятся от оси симметрии, где знак плюс представляет расстояние вправо, а знак минус представляет расстояние влево.

Если бы этот член расстояния уменьшился до нуля, значение оси симметрии было бы значением x единственного нуля, то есть существует только одно возможное решение квадратного уравнения. Алгебраически это означает, что √ b ² - 4 ac = 0 , или просто b ² - 4 ac = 0 (где левая часть называется дискриминантом). Это один из трех случаев, когда дискриминант указывает, сколько нулей будет иметь парабола. Если дискриминант положительный, расстояние будет отличным от нуля, и будет два решения. Однако есть также случай, когда дискриминант меньше нуля, и это означает, что расстояние будет мнимым  - или некоторым кратным комплексной единицы i , где i = √ −1  - и нули параболы будут комплексными числами . Комплексные корни будут комплексно сопряженными , где действительная часть комплексных корней будет значением оси симметрии. Не будет реальных значений x там, где парабола пересекает x-ось.

Размерный анализ [ править ]

Если константы a , b и / или c не являются безразмерными , то единицы x должны быть равны единицамб/а, из-за требования, чтобы ax ² и bx согласовывали свои единицы измерения. Кроме того, по той же логике, единицы c должны быть равны единицамб ²/а, что можно проверить без решения относительно x . Это может быть мощным инструментом для проверки правильности установки квадратичного выражения физических величин до решения этой проблемы.

См. Также [ править ]

• Дискриминантный
• Основная теорема алгебры
• Формулы Виета

Ссылки [ править ]