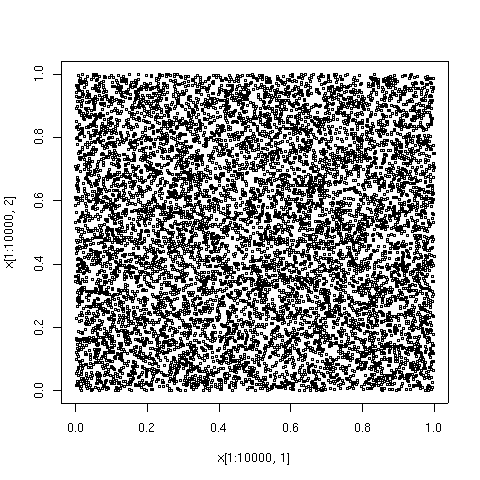
Последовательность с низким расхождением
В математике последовательность с низким расхождением — это последовательность со свойством, что для всех значений N его подпоследовательность x1 ,... , xN имеет низкое расхождение .
Грубо говоря, невязка последовательности мала, если доля точек в последовательности, попадающих в произвольное множество B , близка к пропорциональной мере B , как это было бы в среднем (но не для конкретных выборок) в случае равнораспределенная последовательность . Конкретные определения расхождения различаются в зависимости от выбора B ( гиперсферы , гиперкубы и т. д .) и того, как расхождение для каждого B вычисляется (обычно нормируется) и комбинируется (обычно путем выбора наихудшего значения).
Последовательности с низким расхождением также называются квазислучайными последовательностями из-за их общего использования в качестве замены равномерно распределенных случайных чисел . Модификатор «квази» используется для более четкого обозначения того, что значения последовательности с низким расхождением не являются ни случайными, ни псевдослучайными , но такие последовательности обладают некоторыми свойствами случайных величин, и в некоторых приложениях, таких как метод квази-Монте-Карло, их меньшее расхождение является важным преимуществом.
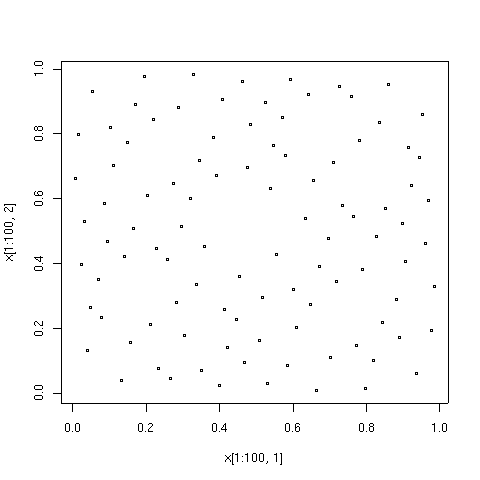
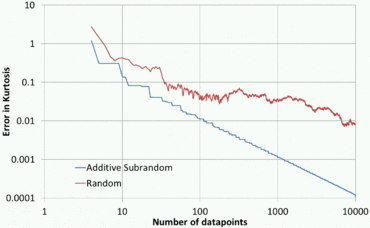
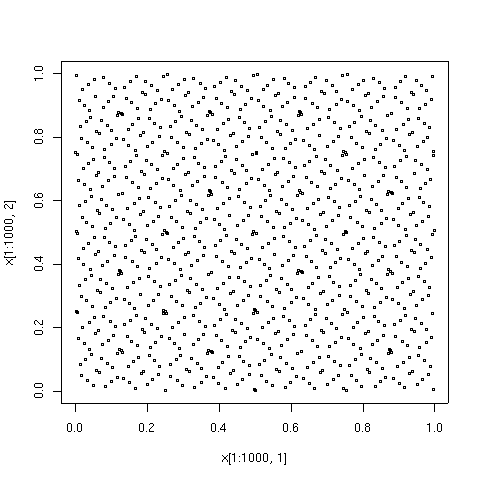
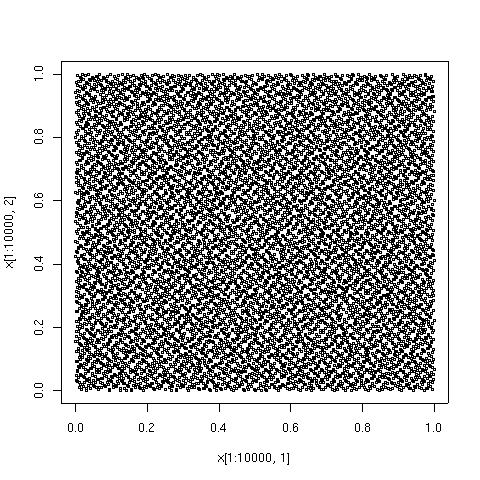
Квазислучайные числа имеют преимущество перед чисто случайными числами в том, что они быстро и равномерно охватывают интересующую область. У них есть преимущество перед чисто детерминированными методами в том, что детерминированные методы дают высокую точность только тогда, когда количество точек данных задано заранее, тогда как при использовании квазислучайных последовательностей точность обычно постоянно улучшается по мере добавления новых точек данных с полным повторным использованием существующих точек. С другой стороны, квазислучайные наборы точек могут иметь значительно меньшее расхождение для заданного числа точек, чем чисто случайные последовательности.
Два полезных приложения заключаются в нахождении характеристической функции функции плотности вероятности и в нахождении производной функции детерминированной функции с небольшим количеством шума. Квазислучайные числа позволяют очень быстро вычислять моменты более высокого порядка с высокой точностью.
Приложения, которые не включают сортировку, могут заключаться в нахождении среднего значения , стандартного отклонения , асимметрии и эксцесса статистического распределения, а также в нахождении интегральных и глобальных максимумов и минимумов сложных детерминированных функций. Квазислучайные числа также можно использовать для обеспечения отправных точек для детерминированных алгоритмов, которые работают только локально, таких как итерация Ньютона-Рафсона .