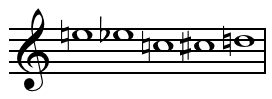Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску
Шесть элементов набор ритмических значений , используемых в Variazioni canoniche от Луиджи Ноно [1]

Набор ( шаг набор , питч-класс набор , набор классы , набор формы , набор рода , коллекция тангажа ) в теории музыки , как и в математике и общем языке, представляет собой совокупность объектов. В музыкальном контексте этот термин традиционно применяется чаще всего к совокупности питчей или питч-классов , но теоретики распространили его использование на другие типы музыкальных объектов, так что можно говорить, например, о наборах длительностей или тембров . [2]

Отличная форма пяти питчевого класса из оперы Игоря Стравинского « Памяти Дилана Томаса» [3]
В наборе 3-1 есть три возможных поворота / инверсии, нормальной формой которых является наименьший пирог или наиболее компактная форма.

Сам по себе набор не обязательно обладает какой-либо дополнительной структурой, например упорядочением или перестановкой . Тем не менее, часто с музыкальной точки зрения важно учитывать наборы, снабженные отношением порядка (называемые сегментами ); в таких контекстах голые наборы часто называют «неупорядоченными», чтобы подчеркнуть. [4]

Двухэлементные наборы называются диадами , трехэлементные наборы трихордами (иногда «триадами», хотя это легко спутать с традиционным значением слова « триада» ). Наборы более высоких мощностей называются тетрахордами (или тетрадами), пентахордами (или пентадами), гексахордами (или гексадами), гептахордами (гептадами или, иногда, смешанными латинскими и греческими корнями, «септахордами»), [5] октахордами (октадами), нонахорды (нонады), декахорды (декады), ундекахорды и, наконец, додекахорд .

Набор временных точек - это набор продолжительности, где расстояние в единицах времени между точками атаки или временными точками - это расстояние в полутонах между классами высоты тона. [6]

Серийный [ править ]

Однако в теории серийной музыки некоторые авторы [ ласковые слова ] (в частности, Милтон Бэббит [7] [ необходима страница ] [ нужна цитата для проверки ] ) используют термин «набор», тогда как другие используют «ряд» или «серию». , а именно для обозначения упорядоченного набора (например, ряда из двенадцати тонов ), используемого для структурирования произведения. Эти авторы [ ласковые слова ] говорят о «двенадцати наборах тонов», «наборах временных точек», «производных наборах» и т. Д. (См. Ниже). Это использование термина «набор» отличается от описанного выше (и упоминается в термине "теория множеств »).

Для этих авторов, [ ласка слово ] установленная форма (или форма строки ) представляет собой конкретное расположение такого Упорядоченного набор: простая форма (исходный порядок), обратное (вверх дно), ретроградная ( в обратном направлении), и ретроградные обратный ( в обратном направлении и вверх ногами). [2]

Производное множество является тот , который генерируется или полученный из последовательных операций на подмножестве, например Веберного «ы концерт , Op.24, в котором последние три подмножеств получены из первых: [8]

{\ override Score.TimeSignature # 'stencil = ## f \ override Score.SpacingSpanner.strict-note-spacing = ## t \ set Score.proportionalNotationDuration = # (ly: make-moment 1/1) \ relative c' ' {\ time 3/1 \ set Score.tempoHideNote = ## t \ tempo 1 = 60 b1 bes d es, g fis aes efc 'cis a}}

Это можно представить в числовом виде как целые числа от 0 до 11:

0 11 3 4 8 7 9 5 6 1 2 10

Первое подмножество (BB ♭ D):

0 11 3 простая форма, интервальная строка = ⟨− 1 + 4⟩

Второе подмножество (E ♭ GF ♯ ) является ретроградно-инверсным по отношению к первому, транспонированному на один полутон вверх:

 3 11 0 ретроградный, интервальная строка = ⟨− 4 + 1⟩ mod 12  3 7 6 инверсия, интервальная строка = ⟨+ 4 −1⟩ mod 12+ 1 1 1 ------= 4 8 7

Третье подмножество (G ♯ EF) ретроградно первого, транспонированного вверх (или вниз) на шесть полутонов:

 3 11 0 ретроградный+ 6 6 6 ------ 9 5 6

И четвертое подмножество (CC ♯ A), обратное первому, транспонировано на один полутон:

 0 11 3 простая форма, интервал-вектор = ⟨− 1 + 4⟩ mod 12  0 1 9 инверсия, интервал-строка = ⟨+ 1 −4⟩ mod 12+ 1 1 1 ------- 1 2 10

Таким образом, каждый из четырех трихордов (наборов из трех нот) отображает взаимосвязь, которая может быть очевидна с помощью любой из четырех операций последовательного ряда, и таким образом создает определенные инварианты . Эти инварианты в последовательной музыке аналогичны использованию общих тонов и общих аккордов в тональной музыке. [ необходима цитата ]

Несерийный [ править ]

Основная статья: Теория множеств (музыка)
Главный секундант на C Play ( помощь · информация ) . 
Незначительный седьмой на C Play ( помощь · информация ) . 
Перевернутая минорная седьмая на C (мажорная секунда на B ♭ ) Игра ( помощь · информация ) . 

Фундаментальная концепция непоследовательного набора состоит в том, что это неупорядоченный набор классов высоты тона . [9]

Нормальная форма набора является самым компактным упорядочение полей в наборе. [10] Томлин определяет «самый компактный» порядок как тот, где «наибольший из интервалов между любыми двумя последовательными шагами находится между первым и последним в списке». [10] Например, набор (0,2) ( большая секунда ) находится в нормальной форме, а набор (0,10) ( второстепенная седьмая , инверсия основной секунды) - нет, его нормальная форма - ( 10,0).

Вместо «исходной» (нетранспонированной, неинвертированной) формы набора простая форма может рассматриваться либо как нормальная форма набора, либо как нормальная форма его инверсии, в зависимости от того, какая из них более плотно упакована. [11] Форте (1973) и Ран (1980) оба перечисляют простые формы множества как наиболее левую возможную версию множества. Forte собирает пачки слева, а Ран - справа («уменьшая маленькие числа», а не делая «большие числа… меньшие» [12] ). В течение многих лет считалось, что существует только пять случаев, когда два алгоритма различаются. [13] Однако в 2017 году теоретик музыки Ян Ринг обнаружил, что существует шестой класс, в котором Форте и Ран 'алгоритмы приходят к разным простым формам.[14] Ян Ринг также установил гораздо более простой алгоритм для вычисления простой формы набора [14], который дает те же результаты, что и более сложный алгоритм, ранее опубликованный Джоном Раном.

Векторы [ править ]

Основная статья: Список наборов питч-класса

См. Также [ править ]

  • Номер Форте
  • Интервал подачи
  • Отношение подобия

Дальнейшее чтение [ править ]

  • Schuijer, Michiel (2008). Анализируя атональную музыку: теория множеств питч-класса и ее контексты . ISBN  978-1-58046-270-9 .

Ссылки [ править ]

  1. ^ Уиттолл, Арнольд (2008). Кембриджское введение в сериализм , стр.165 . Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-68200-8 (PBK). 
  2. ^ a b Виттлих, Гэри (1975). "Наборы и порядок упорядочивания в музыке двадцатого века", Аспекты музыки двадцатого века , с.475. Виттлих, Гэри (ред.). Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. ISBN 0-13-049346-5 . 
  3. ^ Уиттолл (2008), с.127.
  4. ^ Моррис, Роберт (1987). Композиция с питч-классами: теория композиционного дизайна , с.27. Издательство Йельского университета. ISBN 0-300-03684-1 . 
  5. ^ Например, Ран (1980), 140.
  6. ^ Витлих (1975), p.476.
  7. ↑ См. Любые из его работ по двенадцатитонной системе, практически все из которых перепечатаны в «Собрании эссе Милтона Бэббита» , S. Peles et. др., ред. Princeton University Press, 2003. ISBN 0-691-08966-3 . 
  8. ^ Витлих (1975), p.474.
  9. ^ Джон Ран , Основы теории Атональная (НьюЙорк: Longman, Лондон и Торонто: Prentice Hall International, 1980), pp.27-28. ISBN 0-582-28117-2 (Longman); ISBN 0-02-873160-3 (Prentice Hall International). Перепечатано в 1987 г. (Нью-Йорк: Schirmer Books; Лондон: Collier Macmillan, 1980), стр. 27. ISBN 0-02-873160-3 .   
  10. ^ a b Томлин, Джей. "Все о теории множеств: что такое нормальная форма?" , JayTomlin.com .
  11. ^ Томлин, Джей. "Все о теории множеств: что такое простая форма?" , JayTomlin.com .
  12. ^ Нельсон, Пол (2004). « Два алгоритма вычисления первичной формы », ComposerTools.com .
  13. ^ Тсао, Мин (2007). Абстрактные музыкальные интервалы: групповая теория композиции и анализа , стр.99, номер 32. ISBN 9781430308355 . Алгоритмы приведены в Morris, Robert (1991). Заметки для занятий по теории атональной музыки , с.103. Лягушка Пик Музыка. 
  14. ^ а б https://ianring.com/musictheory/scales/#primeform

Внешние ссылки [ править ]

  • "Калькулятор теории множеств" , JayTomlin.com . Вычисляет нормальную форму, простую форму, число Форте и вектор интервального класса для заданного набора и наоборот.
  • " PC Set Калькулятор ", MtA.Ca .