Стоксов дрейф

Пространство плавников вдоль северного побережья штата Вашингтон . Стоксовый дрейф - помимо, например, дрейфа Экмана и геострофических течений - является одним из важных процессов в переносе морского мусора . ^[1]

Стоксы дрейфуют в глубоководных волнах, длина которых примерно в два раза больше глубины воды. Щелкните здесь, чтобы просмотреть анимацию (4,15 МБ).
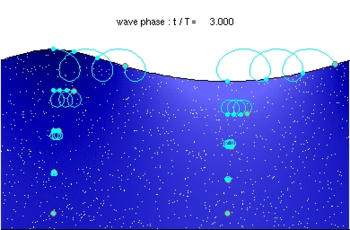
Описание (также анимация) :
Красные кружки - текущие положения безмассовых частиц, движущихся со скоростью потока . Голубая линия показывает путь этих частиц, а голубая линия обводит положение частицы после каждого периода волны . Белые точки - это жидкие частицы, за которыми также следует во времени. В показанном здесь случае средняя эйлерова горизонтальная скорость ниже впадины волны равна нулю.
Обратите внимание, что период волны, испытываемый жидкой частицей вблизи свободной поверхности , отличается от периода волны в фиксированном горизонтальном положении (как показано голубыми кружками). Это связано с доплеровским сдвигом .

Стоксы дрейфуют в мелководных волнах , длина которых намного превышает глубину воды. Щелкните здесь, чтобы просмотреть анимацию (1,29 МБ).
Описание (также анимация) :
Красные кружки - текущие положения безмассовых частиц, движущихся со скоростью потока . Голубая линия показывает путь этих частиц, а голубая линия обводит положение частицы после каждого периода волны . Белые точки - это жидкие частицы, за которыми также следует во времени. В показанном здесь случае средняя эйлерова горизонтальная скорость ниже впадины волны равна нулю.
Обратите внимание, что период волны, испытываемый жидкой частицей вблизи свободной поверхности , отличается от периода волны в фиксированном горизонтальном положении (как показано голубыми кружками). Это связано с доплеровским сдвигом .

Для чистого волнового движения в динамике жидкости , то скорость дрейфа Стокса является средней скоростью , когда после определенной жидкости участка , как он перемещается с потоком текучей среды . Так , например, частица с плавающей на свободную поверхность от воды волн , испытывает скорость дрейфа чистого Стокса в направлении распространения волн .

В более общем плане , скорость дрейфа Стокса представляет собой разность между средней лагранжевой скоростью потока посылки жидкости и средней эйлеровой скоростью потока из жидкости в фиксированном положении. Это нелинейное явление названо в честь Джорджа Габриэля Стоукса , который вывел выражения для этого дрейфа в своем исследовании волн на воде в 1847 году .

Дрейфа Стокса разница в конечных положениях, по истечении заранее определенного периода времени (обычно один период волны ), как получено из описания в функции Лагранжа и Эйлера координат . Конечное положение в лагранжевом описании получается путем отслеживания определенного участка флюида в течение временного интервала. Соответствующее конечное положение в эйлеровом описании получается интегрированием скорости потока в фиксированном положении - равном начальному положению в лагранжевом описании - в течение того же интервала времени.

Скорость стоксова дрейфа равна стоксову дрейфу, деленному на рассматриваемый интервал времени. Часто скорость стоксова дрейфа свободно называют стоксовым дрейфом. Стоксов дрейф может иметь место во всех случаях колебательного течения, неоднородного в пространстве. Например, водные волны , приливы и атмосферные волны .

В лагранжевом описании частицы жидкости могут дрейфовать далеко от своих исходных положений. В результате однозначное определение средней лагранжевой скорости и скорости стоксова дрейфа, которые можно отнести к определенному фиксированному положению, отнюдь не является тривиальной задачей. Однако такое недвусмысленное описание дает теория Обобщенного лагранжевого среднего (GLM) Эндрюса и Макинтайра в 1978 году . ^[2]

Стоксов дрейф важен для массопереноса всех видов материалов и организмов колебательными потоками. Кроме того, дрейф Стокса важен для генерации ленгмюровских циркуляций . ^[3] Для нелинейных и периодических волн на воде точные результаты по стоксовому дрейфу были вычислены и сведены в таблицу. ^[4]

Математическое описание [ править ]

Лагранжиан движение посылки по текучей среде с позиции вектора х = ξ ( & alpha ; , т) в эйлеровых координатах определяется по формуле: ^[5]

${\ displaystyle {\ dot {\ boldsymbol {\ xi}}} \, = \, {\ frac {\ partial {\ boldsymbol {\ xi}}} {\ partial t}} \, = \, {\ boldsymbol { u}} ({\ boldsymbol {\ xi}}, t),}$

где ∂ ξ / ∂t - частная производная от ξ ( α , t) по t , а

ξ ( α , t) - лагранжев вектор положения жидкой посылки,

u ( x , t) - эйлерова скорость ,

x - вектор положения в эйлеровой системе координат ,

α - вектор положения в лагранжевой системе координат ,

т - время .

Часто лагранжевые координаты α выбираются так, чтобы они совпадали с эйлеровыми координатами x в начальный момент времени t = t ₀  : ^[5]

${\ displaystyle {\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t_ {0}) \, = \, {\ boldsymbol {\ alpha}}.}$

Но возможны и другие способы маркировки пакетов с жидкостью.

Если среднее значение величины обозначено чертой сверху, то вектор средней эйлеровой скорости ū _E и средний лагранжев вектор скорости ū _L равны:

${\ displaystyle {\ begin {align} {\ overline {\ boldsymbol {u}}} _ {E} \, & = \, {\ overline {{\ boldsymbol {u}} ({\ boldsymbol {x}}, t)}}, \\ {\ overline {\ boldsymbol {u}}} _ {L} \, & = \, {\ overline {{\ dot {\ boldsymbol {\ xi}}}} ({\ boldsymbol {\ alpha}}, t)}} \, = \, {\ overline {\ left ({\ frac {\ partial {\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t)} {\ partial t}} \ right)}} \, = \, {\ overline {{\ boldsymbol {u}} ({\ boldsymbol {\ xi}} ({\ boldsymbol {\ alpha}}, t), t)}} . \ end {выравнивается}}}$

В зависимости от предмета исследования могут использоваться разные определения среднего , см. Эргодическую теорию :

• среднее время ,
• средняя площадь ,
• средний по ансамблю и
• фазовое среднее.

Скорость стоксова дрейфа ū _S определяется как разница между средней эйлеровой скоростью и средней лагранжевой скоростью: ^[6]

${\displaystyle {\overline {\boldsymbol {u}}}_{S}\,=\,{\overline {\boldsymbol {u}}}_{L}\,-\,{\overline {\boldsymbol {u}}}_{E}.}$

Во многих ситуациях отображение средних величин из некоторой эйлеровой позиции x в соответствующую лагранжевую позицию α представляет собой проблему. Поскольку жидкий участок с меткой α проходит по пути из множества различных эйлеровых позиций x , невозможно присвоить α единственному x . Математически прочная основа для однозначного отображения между средними лагранжевыми и эйлеровыми величинами обеспечивается теорией обобщенного лагранжевого среднего (GLM) Эндрюса и Макинтайра (1978) .

Пример: одномерный сжимаемый поток [ править ]

Для эйлеровой скорости как монохроматической волны любой природы в сплошной среде: легко получить по теории возмущений - с малым параметром - для положения частицы${\displaystyle u={\hat {u}}\sin \left(kx-\omega t\right),}$${\displaystyle k{\hat {u}}/\omega }$${\displaystyle x=\xi (\xi _{0},t):}$

${\displaystyle {\dot {\xi }}=\,{u}({\xi },t)={\hat {u}}\sin \,\left(k\xi -\omega t\right),}$

${\displaystyle \xi (\xi _{0},t)\approx \xi _{0}+{\frac {\hat {u}}{\omega }}\cos(k\xi _{0}-\omega t)-{\frac {1}{4}}{\frac {k{\hat {u}}^{2}}{\omega ^{2}}}\sin 2(k\xi _{0}-\omega t)+{\frac {1}{2}}{\frac {k{\hat {u}}^{2}}{\omega }}t.}$

Здесь последнее слагаемое описывает скорость стоксова дрейфа ^[7]${\displaystyle {\tfrac {1}{2}}k{\hat {u}}^{2}/\omega .}$

Пример: волны на глубокой воде [ править ]

В Стоксе дрейф был сформулирован для водных волн от Джорджа Габриэля Стокса в 1847. Для простоты, случай бесконечного -deep воды рассматриваются, с линейным распространением волн в виде синусоидальной волны на свободную поверхность слоя жидкости: ^[8]

${\displaystyle \eta \,=\,a\,\cos \,\left(kx-\omega t\right),}$

куда

η является высотой от свободной поверхности в г -направления (м),

а - амплитуда волны (в метрах),

k - волновое число : k = 2π / λ ( радиан на метр),

ω - угловая частота : ω = 2π / T ( радиан в секунду ),

x - горизонтальная координата и направление распространения волны (в метрах),

z - вертикальная координата с положительным направлением z, указывающим из слоя жидкости (в метрах),

λ - длина волны (в метрах), а

T - период волны ( секунды ).

Как показано ниже, горизонтальная составляющая ū _S ( z ) скорости стоксова дрейфа для глубоководных волн приблизительно равна: ^[9]

${\displaystyle {\overline {u}}_{S}\,\approx \,\omega \,k\,a^{2}\,{\text{e}}^{2kz}\,=\,{\frac {4\pi ^{2}\,a^{2}}{\lambda \,T}}\,{\text{e}}^{4\pi \,z/\lambda }.}$

Как видно, стоксова дрейфовая скорость ū _S является нелинейной величиной в терминах амплитуды волны a . Кроме того, скорость стоксова дрейфа экспоненциально спадает с глубиной: на глубине четверти длины волны, z = -¼ λ , она составляет около 4% от ее значения на средней свободной поверхности , z = 0 .

Вывод [ править ]

Предполагается, что волны имеют бесконечно малую амплитуду, а свободная поверхность колеблется около среднего уровня z = 0 . Эти волны распространяются под действием силы тяжести, с постоянным ускорением вектором с помощью силы тяжести (указывая вниз в отрицательном г -направления). Далее предполагается, что жидкость невязкая ^[10] и несжимаемая с постоянной плотностью массы . Жидкости поток является безвихревым . На бесконечной глубине жидкость считается покоящейся..

Теперь поток может быть представлен потенциалом скорости φ , удовлетворяющим уравнению Лапласа и ^[8]

${\displaystyle \varphi \,=\,{\frac {\omega }{k}}\,a\;{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right).}$

Для того чтобы иметь нетривиальное решение для этого собственных значений проблемы, длина волны и период волны не могут быть выбраны произвольно, но должны удовлетворять глубоководное дисперсии соотношения: ^[11]

${\displaystyle \omega ^{2}\,=\,g\,k.}$

с г на ускорение по тяжести в ( м / с ² ). В рамках линейной теории горизонтальная и вертикальная составляющие ξ _x и ξ _z, соответственно, лагранжевой позиции ξ равны: ^[9]

${\displaystyle {\begin{aligned}\xi _{x}\,&=\,x\,+\,\int \,{\frac {\partial \varphi }{\partial x}}\;{\text{d}}t\,=\,x\,-\,a\,{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right),\\\xi _{z}\,&=\,z\,+\,\int \,{\frac {\partial \varphi }{\partial z}}\;{\text{d}}t\,=\,z\,+\,a\,{\text{e}}^{kz}\,\cos \,\left(kx-\omega t\right).\end{aligned}}}$

Горизонтальная составляющая ū _S дрейфовой скорости Стокса оценивается с помощью разложения Тейлора вокруг x эйлеровой компоненты горизонтальной скорости u _x = ∂ξ _x / ∂t в позиции ξ  : ^[5]

${\displaystyle {\begin{aligned}{\overline {u}}_{S}\,&=\,{\overline {u_{x}({\boldsymbol {\xi }},t)}}\,-\,{\overline {u_{x}({\boldsymbol {x}},t)}}\,\\&=\,{\overline {\left[u_{x}({\boldsymbol {x}},t)\,+\,\left(\xi _{x}-x\right)\,{\frac {\partial u_{x}({\boldsymbol {x}},t)}{\partial x}}\,+\,\left(\xi _{z}-z\right)\,{\frac {\partial u_{x}({\boldsymbol {x}},t)}{\partial z}}\,+\,\cdots \right]}}-\,{\overline {u_{x}({\boldsymbol {x}},t)}}\\&\approx \,{\overline {\left(\xi _{x}-x\right)\,{\frac {\partial ^{2}\xi _{x}}{\partial x\,\partial t}}}}\,+\,{\overline {\left(\xi _{z}-z\right)\,{\frac {\partial ^{2}\xi _{x}}{\partial z\,\partial t}}}}\\&=\,{\overline {{\bigg [}-a\,{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right){\bigg ]}\,{\bigg [}-\omega \,k\,a\,{\text{e}}^{kz}\,\sin \,\left(kx-\omega t\right){\bigg ]}}}\,\\&+\,{\overline {{\bigg [}a\,{\text{e}}^{kz}\,\cos \,\left(kx-\omega t\right){\bigg ]}\,{\bigg [}\omega \,k\,a\,{\text{e}}^{kz}\,\cos \,\left(kx-\omega t\right){\bigg ]}}}\,\\&=\,{\overline {\omega \,k\,a^{2}\,{\text{e}}^{2kz}\,{\bigg [}\sin ^{2}\,\left(kx-\omega t\right)+\cos ^{2}\,\left(kx-\omega t\right){\bigg ]}}}\\&=\,\omega \,k\,a^{2}\,{\text{e}}^{2kz}.\end{aligned}}}$

См. Также [ править ]

• Сила Кориолиса-Стокса
• Дарвин дрейф
• Лагранжевы и эйлеровы координаты
• Существенная производная

Ссылки [ править ]

Исторический [ править ]

• ДОБАВИТЬ Крейк (2005). «Джордж Габриэль Стоукс по теории водных волн». Ежегодный обзор гидромеханики . 37 (1): 23–42. Bibcode : 2005AnRFM..37 ... 23С . DOI : 10.1146 / annurev.fluid.37.061903.175836 .
• Г. Г. Стоукс (1847). «К теории колебательных волн». Труды Кембриджского философского общества . 8 : 441–455.
  Перепечатано в: GG Stokes (1880). Математический и физический Papers, Том I . Издательство Кембриджского университета. С. 197–229.

Другое [ править ]

• Д. Г. Эндрюс и М. Е. Макинтайр (1978). «Точная теория нелинейных волн на лагранжевом среднем течении». Журнал гидромеханики . 89 (4): 609–646. Bibcode : 1978JFM .... 89..609A . DOI : 10.1017 / S0022112078002773 .
• ДОБАВИТЬ Крейк (1985). Волновые взаимодействия и потоки жидкости . Издательство Кембриджского университета. ISBN 978-0-521-36829-2.
• М. С. Лонге-Хиггинс (1953). «Массовый транспорт в водных волнах». Философские труды Королевского общества А . 245 (903): 535–581. Bibcode : 1953RSPTA.245..535L . DOI : 10.1098 / rsta.1953.0006 .
• Филлипс, О.М. (1977). Динамика верхнего слоя океана (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-29801-8.
• Г. Фалькович (2011). Механика жидкости (краткий курс для физиков) . Издательство Кембриджского университета. ISBN 978-1-107-00575-4.
• Кубота, М. (1994). «Механизм накопления плавающего морского мусора к северу от Гавайев». Журнал физической океанографии . 24 (5): 1059–1064. Bibcode : 1994JPO .... 24.1059K . DOI : 10,1175 / 1520-0485 (1994) 024 <1059: AMFTAO> 2.0.CO; 2 .

Примечания [ править ]