Симметричная моноидальная категория

В теории категорий , разделе математики , симметричная моноидальная категория - это моноидальная категория (т. Е. Категория, в которой определено «тензорное произведение» ), такая, что тензорное произведение является симметричным (т. Е. В определенном строгом смысле естественно изоморфным для всех объектов и категории). Одним из типичных примеров симметричной моноидальной категории является категория векторных пространств над некоторым фиксированным полем k, использующая обычное тензорное произведение векторных пространств . ${\ displaystyle \ otimes}$${\ displaystyle A \ otimes B}$${\ displaystyle B \ otimes A}$${\ displaystyle A}$${\ displaystyle B}$

Определение [ править ]

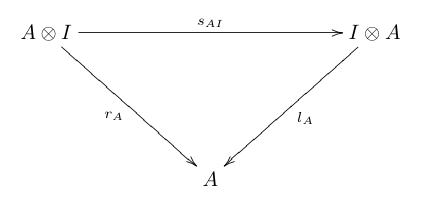
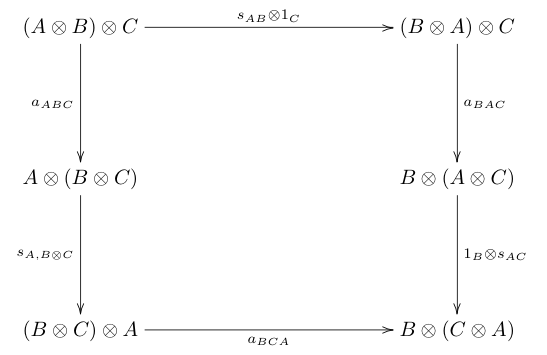
Симметричная моноидальная категория - это моноидальная категория ( C , ⊗, I ) такая, что для каждой пары A , B объектов в C существует изоморфизм , естественный как для A, так и для B и такой, что следующие диаграммы коммутируют:${\ displaystyle s_ {AB}: от A \ otimes B \ до B \ otimes A}$

• Связность агрегата:

  

• Связность ассоциативности:

  

• Обратный закон:

  

На диаграммах выше a , l , r - изоморфизм ассоциативности, левый единичный изоморфизм и правый единичный изоморфизм соответственно.

Примеры [ править ]

Некоторые примеры и не примеры симметричных моноидальных категорий:

• Категория множеств . Тензорное произведение - это декартово теоретико-множественное произведение, и любой синглтон можно зафиксировать как единичный объект.
• Категория групп . Как и раньше, тензорное произведение - это просто декартово произведение групп, а тривиальная группа - это единичный объект.
• В более общем смысле любая категория с конечными произведениями, то есть декартова моноидальная категория , является симметричной моноидальной. Тензорное произведение является прямым произведением объектов, а любой конечный объект (пустой продукт) является единичным объектом.
• Категория бимодулей над кольцом R является моноидальной ( с помощью обычного тензорного произведения модулей), но не обязательно симметричен. Если R коммутативно, категория левых R -модулей симметрична моноидальна. Последний примерный класс включает категорию всех векторных пространств над данным полем.
• Для поля k и группы (или алгебры Ли над k ) категория всех k- линейных представлений группы (или алгебры Ли) является симметричной моноидальной категорией. Здесь используется стандартное тензорное произведение представлений.
• Категории ( Ste , ) и ( Ste , ) стереотипных пространств над симметричными моноидальными, и, более того, ( Ste , ) является замкнутой симметричной моноидальной категорией с внутренним гом-функтором .${\ displaystyle \ circledast}$${\ displaystyle \ odot}$${\ Displaystyle {\ mathbb {C}}}$${\ displaystyle \ circledast}$${\ displaystyle \ oslash}$

Свойства [ править ]

Классифицирующее пространство (геометрическая реализация нерва ) симметричной моноидальной категория является пространством, поэтому его завершение группы представляет собой бесконечное пространство петель . ^[1]${\displaystyle E_{\infty }}$

Специализации [ править ]

Крестик симметричная моноидалъная категорией является симметричными моноидальными категориями с совместимой структурой кинжала .

А космос является полным cocomplete закрыт симметричной моноидалъной категорией.

Обобщения [ править ]

В симметричной моноидальной категории естественные изоморфизмы сами себе обратны в том смысле, что . Если мы откажемся от этого требования (но все же потребуем, чтобы оно было естественно изоморфно ), мы получим более общее понятие сплетенной моноидальной категории .${\displaystyle s_{AB}:A\otimes B\to B\otimes A}$${\displaystyle s_{BA}\circ s_{AB}=1_{A\otimes B}}$${\displaystyle A\otimes B}$${\displaystyle B\otimes A}$

Ссылки [ править ]

• Симметричная моноидальная категория в nLab
• Эта статья включает материал из категории «Симметричные моноидальные» на PlanetMath , которая находится под лицензией Creative Commons Attribution / Share-Alike License .