Равный темперамент
Равная темперация - это музыкальная темперация или система настройки , которая аппроксимирует только интервалы , разделяя октаву (или другой интервал) на равные шаги. Это означает, что соотношение частот любой соседней пары нот одинаково, что дает одинаковый воспринимаемый размер шага, поскольку высота звука воспринимается примерно как логарифм частоты. [2]
В классической музыке и западной музыке в целом наиболее распространенной системой настройки с 18 века была двенадцатитоновая равная темперация (также известная как 12 равных темпераций , 12-TET или 12-ET ; неофициально сокращенно до двенадцати равных ), которая делит октаву на 12 частей, все из которых равны по логарифмической шкале , с отношением, равным 12-му корню из 2 ( 12 √ 2 ≈ 1,05946). Полученный в результате наименьший интервал, равный 1/12 ширины октавы, называется полутоном или полушагом . В западных странахтермин равный темперамент без оговорок обычно означает 12-TET.
В наше время 12-TET обычно настраивают относительно стандартной высоты тона 440 Гц, называемой A440 , что означает, что одна нота A настроена на 440 герц , а все остальные ноты определяются как несколько кратных полутонов, кроме нее, либо выше. или ниже по частоте . Стандартная высота тона не всегда была 440 Гц. Он менялся и в целом повышался за последние несколько сотен лет. [3]
Другие равные темпераменты делят октаву по-разному. Например, некоторая музыка была написана в 19-TET и 31-TET , в то время как в арабской системе тонов используется 24-TET.
Вместо того, чтобы делить октаву, одинаковая темперация может также делить другой интервал, как равномерная версия шкалы Болена-Пирса , которая делит только интервал октавы и квинты (соотношение 3:1), называемый « тритава» или « псевдооктава » в этой системе на 13 равных частей.
Для систем настройки, которые делят октаву поровну, но не являются аппроксимацией только интервалов, можно использовать термин равное деление октавы или EDO .
Струнные ансамбли без ладов , которые могут регулировать настройку всех нот, кроме открытых струн , и вокальные группы, у которых нет ограничений по механической настройке, иногда используют настройку, намного более близкую к интонации, по акустическим причинам. Другие инструменты, такие как некоторые духовые , клавишные и ладовые инструменты, часто имеют лишь приблизительно равную темперацию, где технические ограничения не позволяют точно настроить. [4] Некоторые духовые инструменты, которые могут легко и спонтанно изменить свой тон, в первую очередь тромбоны , используют настройку, аналогичную струнным ансамблям и вокальным группам.
Общие свойства
В этом разделе не цитируются никакие источники . ( июнь 2011 г. ) |
В равной темперации расстояние между двумя соседними ступенями гаммы составляет один и тот же интервал . Поскольку воспринимаемая идентичность интервала зависит от его отношения , эта шкала с четными шагами представляет собой геометрическую последовательность умножений. ( Арифметическая последовательность интервалов не будет звучать равномерно и не позволит транспонировать в разные тональности.) В частности, наименьший интервал в равнотемперированной гамме - это соотношение:
где отношение r делит отношение p (обычно октаву , равное 2:1) на n равных частей. ( См . Ниже двенадцатитоновую равную темперацию . )
Весы часто измеряются в центах , которые делят октаву на 1200 равных интервалов (каждый называется цент). Эта логарифмическая шкала упрощает сравнение различных систем настройки, чем сравнение соотношений, и находит широкое применение в этномузыкологии . Базовый шаг в центах для любого равного темперамента можно найти, взяв ширину p выше в центах (обычно октава, ширина которой составляет 1200 центов), называемую ниже w , и разделив ее на n частей:
В музыкальном анализе материалу, принадлежащему к равной темперации, часто присваивается целочисленное обозначение , что означает, что для представления каждой высоты тона используется одно целое число. Это упрощает и обобщает обсуждение основного материала в темперации точно так же, как логарифмирование умножения сводит его к сложению. Кроме того, применяя модульную арифметику , где модуль представляет собой количество делений октавы (обычно 12), эти целые числа можно свести к классам высоты тона , что устраняет различие (или признает сходство) между высотами с одинаковыми именами, например c равно 0 независимо от октавного регистра. МИДИ _ стандарт кодирования использует целочисленные обозначения нот.
Общие формулы равнотемперированного интервала
В этом разделе отсутствует информация об общих формулах равнотемперированного интервала. ( февраль 2019 г. ) |
Двенадцатитоновая ровная темперация
12-тональная равномерная темперация, которая делит октаву на двенадцать интервалов одинакового размера, является наиболее распространенной музыкальной системой, используемой сегодня, особенно в западной музыке.
История
Двум фигурам, которым часто приписывают достижение точного расчета равного темперамента, являются Чжу Цзайю (также латинизированный как Чу-Цайю. Китайский:朱 載 堉) в 1584 году и Саймон Стевин в 1585 году. Согласно Фрицу А. Каттнеру, критику теории, [5] известно, что «Чу-Цайю представил в 1584 году очень точный, простой и остроумный метод арифметического вычисления равнотемперированных моноаккордов» и что «Саймон Стевин предложил математическое определение одинаковой темперации плюс несколько менее точное вычисление соответствующих числовых значений в 1585 году или позднее». События происходили независимо. [6]
Кеннет Робинсон приписывает изобретение равного темперамента Чжу Зайю [7] и приводит текстовые цитаты в качестве доказательства. [8] Zhu Zaiyu цитируется, что в тексте, датированном 1584 годом, «я основал новую систему. Я устанавливаю одну ногу как число, из которого должны быть извлечены другие, и используя пропорции, я извлекаю их. нужно найти точные цифры для волынщиков за двенадцать операций». [8] Каттнер не согласен и отмечает, что его утверждение «не может считаться правильным без серьезных оговорок». [5] Каттнер предполагает, что ни Чжу Зайю, ни Саймон Стевин не достигли одинакового темперамента и что ни один из них не должен рассматриваться как изобретатель. [9]
Китай
В то время как Китай ранее придумал приближения для 12-TET, Чжу Зайюй был первым человеком, который математически решил двенадцатитоновую равную темперацию, [10] которую он описал в своем Слиянии музыки и календаря 律暦融通в 1580 году и Полный сборник Музыка и звук ( Yuelü quan shu 樂律全書) в 1584 году . [11] Расширенный отчет также дает Джозеф Нидхэм. [12] Чжу получил свой результат математически, последовательно разделив длину струны и трубы на 12 √ 2 ≈ 1,059463, а длину трубы на 24 √ 2 , [13] таким образом, что после двенадцати делений (октава) длина делится в 2 раза.
Чжу Зайю создал несколько инструментов, настроенных на его систему, в том числе бамбуковые дудки. [14]
Европа
Одними из первых европейцев, выступивших за равный темперамент, были лютнисты Винченцо Галилей , Джакомо Горзанис и Франческо Спиначино , все из которых написали музыку на нем. [15] [16] [17] [18]
Саймон Стевин был первым, кто разработал 12-TET на основе двенадцатого корня из двух , который он описал в книге Van De Spiegheling der singconst (ок. 1605 г.), опубликованной посмертно почти три столетия спустя, в 1884 г. [19]
На протяжении нескольких столетий в Европе использовались различные системы настройки, в том числе 12 равнотемперированных, а также подразумеваемая темперация и хорошо темперированная , каждую из которых можно рассматривать как аппроксимацию первой. Исполнители на щипковых инструментах (лютнисты и гитаристы) обычно предпочитали равный темперамент, [20] в то время как другие были более разделены. [21] В конце концов победила двенадцатитоновая равномерная темперация. Это позволило новым стилям симметричной тональности и политональности , атональной музыке , такой как написанная с помощью техники двенадцати тонов или сериализма , и джазу (по крайней мере, его фортепианному компоненту) развиваться и процветать.
Математика
В двенадцатитоновой равной темперации, которая делит октаву на 12 равных частей, ширина полутона , т. е. отношение частот интервала между двумя соседними нотами, есть корень двенадцатой степени из двух :
Это эквивалентно:
Этот интервал делится на 100 центов .
Расчет абсолютных частот
Чтобы найти частоту P n ноты в 12-TET, можно использовать следующее определение:
В этой формуле Pn относится к высоте тона или частоте (обычно в герцах ), которую вы пытаетесь найти. P a относится к частоте эталонного основного тона. n и a относятся к номерам, присвоенным желаемому шагу и эталонному шагу соответственно. Эти два числа взяты из списка последовательных целых чисел, присвоенных последовательным полутонам. Например, A 4 (опорная высота тона) — это 49-я клавиша с левого края фортепиано (настроенного на 440 Гц ), а C 4 ( средняя C ) и F# 4 — это 40-я и 46-я клавиши соответственно. Эти числа можно использовать для нахождения частоты C4 и фа-диез 4 :
Преобразование частот в их аналоги с равной темперацией
Чтобы преобразовать частоту (в Гц) в ее эквивалент 12-TET, можно использовать следующую формулу:
Где E n относится к частоте основного тона в равной темперации, а a относится к частоте эталонного основного тона. Например, (если мы примем базовую высоту звука равной 440 Гц), мы увидим, что E 5 и C# 5 равны следующим частотам соответственно:
Сравнение только с интонацией
Интервалы 12-TET близки к некоторым интервалам только по интонации . [22] Квинты и четверти почти неразличимо близки к интервалам, а терции и шестые — дальше.
В следующей таблице размеры различных справедливых интервалов сравниваются с их равномерными аналогами, представленными как в соотношении, так и в центах .
| Название интервала | Точное значение в 12-тет | Десятичное значение в 12-ТЕТ | центов | Просто интонационный интервал | Центов просто интонация | Разница |
|---|---|---|---|---|---|---|
| Унисон ( С ) | 2 0 ⁄ 12 = 1 | 1 | 0 | 1 ⁄ 1 = 1 | 0 | 0 |
| Незначительная секунда ( D ♭ ) | 2 1 ⁄ 12 = 12 √ 2 | 1.059463 | 100 | 16 ⁄ 15 = 1,06666… | 111,73 | -11,73 |
| Большая секунда ( D ) | 2 2 ⁄ 12 = 6 √ 2 | 1.122462 | 200 | 9 ⁄ 8 = 1,125 | 203,91 | -3,91 |
| Малая треть ( E ♭ ) | 2 3 ⁄ 12 = 4 √ 2 | 1.189207 | 300 | 6 ⁄ 5 = 1,2 | 315,64 | -15,64 |
| Большая треть ( E ) | 2 4 ⁄ 12 = 3 √ 2 | 1.259921 | 400 | 5 ⁄ 4 = 1,25 | 386,31 | +13,69 |
| Идеальная четвертая ( F ) | 2 5 ⁄ 12 = 12 √ 32 | 1.33484 | 500 | 4 ⁄ 3 = 1,33333… | 498.04 | +1,96 |
| Тритон ( G ♭ ) | 2 6 ⁄ 12 = √ 2 | 1.414214 | 600 | 64 ⁄ 45 = 1,42222… | 609,78 | -9,78 |
| Идеальная пятая ( G ) | 2 7 ⁄ 12 = 12 √ 128 | 1.498307 | 700 | 3 ⁄ 2 = 1,5 | 701,96 | -1,96 |
| Незначительная шестая ( A ♭ ) | 2 8 ⁄ 12 = 3 √ 4 | 1.587401 | 800 | 8 ⁄ 5 = 1,6 | 813,69 | -13,69 |
| Большая шестая ( A ) | 2 9 ⁄ 12 = 4 √ 8 | 1.681793 | 900 | 5 ⁄ 3 = 1,66666… | 884,36 | +15,64 |
| Малая седьмая ( B ♭ ) | 2 · 10 ⁄ 12 = 6 √ 32 | 1.781797 | 1000 | 16 ⁄ 9 = 1,77777… | 996.09 | +3,91 |
| Большая седьмая ( B ) | 2 · 11 ⁄ 12 = 12 √ 2048 | 1.887749 | 1100 | 15 ⁄ 8 = 1,875 | 1088.270 | +11,73 |
| Октава ( С ) | 2 12 ⁄ 12 = 2 | 2 | 1200 | 2 ⁄ 1 = 2 | 1200.00 | 0 |
Семитоновое равное деление квинты
Скрипки, альты и виолончели настроены в чистых квинтах (соль — ре — ля — ми для скрипок и до — соль — ре — ля для альтов и виолончелей), что говорит о том, что их полутоновое отношение несколько выше, чем в обычная двенадцатитоновая равномерная темперация. Поскольку чистая квинта находится в отношении 3:2 к своему основному тону, и этот интервал состоит из 7 шагов, каждый тон находится в отношении 7 √ 3 ⁄ 2 к следующему (100,28 цента), что обеспечивает чистую квинту. с соотношением 3: 2, но слегка расширенной октавой с соотношением ≈ 517: 258 или ≈ 2,00388: 1, а не с обычным соотношением 2: 1, потому что двенадцать полных квинтов не равны семи октавам. [23] Однако во время реальной игры скрипач выбирает высоту тона на слух, и только четыре непрерывных тона струн гарантированно демонстрируют это соотношение 3: 2.
Другие равные темпераменты
5- и 7-тональные темпераменты в этномузыкологии
Пять и семь тонов одинаковой темперации ( 5-TET Play ( help · info ) и 7-TET Play ( help · info ) ), с 240 Play ( help · info ) и 171 Play ( help · info ) центовыми шагами соответственно, являются довольно общий.
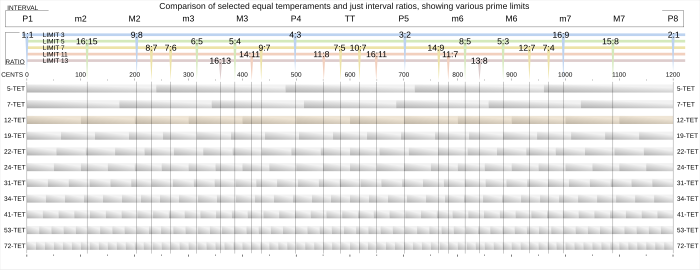
5-TET и 7-TET отмечают конечные точки допустимого диапазона настройки синтонной темперации , как показано на рисунке 1 .
- В 5-TET темперированная совершенная квинта имеет ширину 720 центов (в верхней части континуума настройки) и отмечает конечную точку континуума настройки, в которой ширина малой секунды сокращается до ширины 0 центов.
- В 7-TET темперированная совершенная квинта имеет ширину 686 центов (в нижней части континуума настройки) и отмечает конечную точку континуума настройки, в которой малая секунда расширяется до ширины большой секунды (по 171 центу каждая). ).
5-тональная ровная темперация
Индонезийские гамеланы настроены на 5-TET согласно Кунсту (1949), но согласно Худу (1966) и МакФи (1966) их настройка сильно различается, и согласно Тенцеру (2000) они содержат растянутые октавы . В настоящее время общепризнано, что из двух основных систем настройки в музыке гамелана, слендро и пелог , только слендро несколько напоминает пятитоновую равную темперацию, в то время как пелог крайне неравномерен; однако Surjodiningrat et al. (1972) проанализировал пелог как подмножество из семи нот девятитоновой равной темперации ( игра за 133 цента ) .
7-тональная ровная темперация
Тайский ксилофон, измеренный Мортоном (1974), «отклонялся только плюс-минус 5 центов» от 7-TET . По словам Мортона, «тайские инструменты с фиксированной высотой звука настроены на эквидистантную систему из семи высот на октаву ... Однако, как и в западной традиционной музыке, все высоты тона системы настройки не используются в одном режиме (часто называемом « масштаб'); в тайской системе пять из семи используются в основных тонах в любом ладе, таким образом устанавливая образец неэквидистантных интервалов для лада». [24] Играть ( помощь · информация )
Гамма южноамериканских индейцев из доинструментальной культуры, измеренная Бойлзом (1969), отличалась семитональной равной темперацией в 175 центов, которая немного растягивает октаву, как в инструментальной музыке гамелана.
В китайской музыке традиционно используется 7-TET. [25] [26]
Различные равные темпераменты
Этот раздел нуждается в дополнительных ссылках для проверки . ( март 2020 г. ) |
19 EDO известен, и некоторые инструменты настроены в 19 EDO. У него немного более плоская идеальная квинта (695 центов), но его большая шестая менее чем на один цент отличается от основной шестой интонации (884 цента). Его малая терция также меньше цента от интонации. (Самый низкий EDO, который дает лучшую минорную треть и большую шестую, чем 19 EDO, - это 232 EDO.) Его совершенная четвертая (505 центов) составляет всего 5 центов диез, чем просто интонация, и 3 цента диез от 12-тет.
23 EDO является самым большим EDO, который не может аппроксимировать 3-ю, 5-ю, 7-ю и 11-ю гармоники (3:2, 5:4, 7:4, 11:8) в пределах 20 центов, что делает его привлекательным для микротоналистов, ищущих необычный микротональный звук. гармоничная территория.
24 EDO , четвертьтоновая шкала(или 24-TET) был популярным микротональным строем в 20-м веке, вероятно, потому, что он представлял собой удобную точку доступа для композиторов, основанных на стандартной западной 12 EDO высоте тона и нотной практике, которые также интересовались микротональностью. Поскольку 24 EDO содержат все ноты 12 EDO, а также новые ноты посередине между каждой соседней парой из 12 нот EDO, они могут использовать дополнительные цвета без потери какой-либо тактики, доступной в 12-тональной гармонии. Тот факт, что 24 кратно 12, также упростил инструментальное достижение 24 EDO за счет использования двух традиционных инструментов 12 EDO, специально настроенных на четверть тона друг от друга, например двух фортепиано, что также позволяло каждому исполнителю (или одному исполнителю, играющему на другом фортепиано). каждой рукой) читать знакомую 12-тональную нотацию.Различные композиторы, в том числе Чарльз Айвз, экспериментировали с музыкой для четвертьтонового фортепиано. 24 EDO очень хорошо аппроксимирует 11-ю гармонику, в отличие от 12 EDO.
26 EDO — это наименьший EDO, почти полностью настраивающий 7-ю гармонику (7:4). Это также очень плоская средняя темперация, что означает, что после 4 квинт получается нейтральная терция, а не мажорная. 26 EDO имеет две второстепенные терции и две второстепенные сексты. На первый взгляд это может немного сбить с толку, потому что если вы играете нейтральную терцию, она звучит как очень плоская мажорная. 26EDO может быть альтернативным темпераментом барбершопской гармонии.
27 EDO — это наименьший EDO, однозначно представляющий все интервалы, включающие первые восемь гармоник. Он смягчает семеричную запятую , но не синтоническую запятую .
29 EDO — это наименьшее количество равных делений октавы, при котором совершенная квинта получается лучше, чем при 12 EDO. Его большая треть примерно так же неточна, как 12-TET; однако он настроен на 14 центов ровно, а не на 14 центов резко. Он также настраивает 7-ю, 11-ю и 13-ю гармоники примерно на одинаковую величину. Это означает, что такие интервалы, как 7:5, 11:7, 13:11 и т. д., очень хорошо сочетаются в 29-TET.
31 EDO отстаивали Христиан Гюйгенс и Адриан Фоккер . 31 EDO имеет немного менее точную квинту, чем 12 EDO, но обеспечивает почти только основные трети и обеспечивает приличное совпадение для гармоник по крайней мере до 13, из которых седьмая гармоника особенно точна.
34 ЭДО дает несколько меньшие суммарные комбинированные ошибки аппроксимации 5-предельных справедливых соотношений 3:2, 5:4, 6:5 и их инверсий, чем 31 ЭДО, хотя аппроксимация 5:4 хуже. 34 EDO не аппроксимирует отношения, включающие простые 7. Он содержит тритон в 600 центов, так как это EDO с четным номером.
41 EDO - это второе наименьшее количество равных делений, которое дает лучшую идеальную квинту, чем 12 EDO. Его большая треть точнее, чем 12 EDO и 29 EDO, примерно на 6 центов. Это не означает один, поэтому он различает 10:9 и 9:8, в отличие от 31edo. Он более точен в 13-пределе, чем 31edo.
46 EDO обеспечивает слегка острые мажорные терции и совершенные квинты, придавая трезвучиям характерное яркое звучание. Гармоники до 11 аппроксимируются с точностью до 5 центов, а 10: 9 и 9: 5 отстают от чистых на одну пятую цента. Поскольку это не единая система, она различает 10:9 и 9:8.
53 EDO лучше аппроксимирует традиционные правильные созвучия , чем 12, 19 или 31 EDO, но используется лишь изредка. Чрезвычайно хорошие идеальные квинты делают его взаимозаменяемым с расширенным пифагорейским строем , но он также приспосабливается к раскольническому темпераменту и иногда используется в теории турецкой музыки . Однако он не соответствует требованиям среднего темперамента, который делает хорошие терции легко достижимыми через цикл квинтов. В 53 EDO очень согласные терции будут достигаться вместо этого с помощью пифагорейской уменьшенной четверти (CF ♭ ), поскольку это пример раскольнического темперамента , как и 41 EDO.
72 EDO хорошо аппроксимирует многие интонационные интервалы, даже в пределах 7 и 11, таких как 7: 4, 9: 7, 11: 5, 11: 6 и 11: 7. 72 ЭДО преподавали, писали и исполняли на практике Джо Манери и его ученики (чьи атональные склонности обычно избегают каких-либо ссылок на интонацию) .что угодно). Его можно считать расширением 12 EDO, потому что 72 кратно 12. 72 EDO имеет наименьший интервал, который в шесть раз меньше наименьшего интервала 12 EDO, и поэтому содержит шесть копий 12 EDO, начинающихся на разных высотах. Он также содержит три копии 24 EDO и две копии 36 EDO, которые сами по себе кратны 12 EDO. 72 EDO также подвергался критике за избыточность из-за сохранения плохих приближений, содержащихся в 12 EDO, несмотря на то, что они не нужны для каких-либо нижних пределов только интонации (например, 5-предел).
96 EDO аппроксимирует все интервалы в пределах 6,25 цента, что едва различимо. Поскольку число кратно 12, оно может использоваться полностью, как обычное 12 EDO. За это выступали несколько композиторов, особенно Хулиан Каррильо с 1924 по 1940-е годы. [28]
Другие равные подразделения октавы, которые нашли случайное использование, включают 15 EDO , 17 EDO и 22 EDO .
2, 5, 12, 41, 53, 306, 665 и 15601 являются знаменателями первых подходящих чисел журнала 2 (3), поэтому 2, 5, 12, 41, 53, 306, 665 и 15601 являются двенадцатыми (и пятыми), т.е. в соответствующих равных темперациях, равных целому числу октав, являются лучшим приближением 2, 5, 12, 41, 53, 306, 665 и 15601 всего двенадцатых/пятых, чем для любых равных темпераций с меньшим количеством тонов. [29] [30]
1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (последовательность A060528 в OEIS ) — это последовательность делений октавы, которые все лучше и лучше приближают идеальную квинту. Связанные последовательности содержат деления, аппроксимирующие другие интервалы. [31]
Это приложение: [1] вычисляет частоты, приблизительные центы и значения изгиба высоты тона MIDI для любых систем с равным делением октавы. Обратите внимание, что «округленный» и «напольный» дают одно и то же значение изменения высоты тона MIDI.
Равные темпераменты неоктавных интервалов
Равнотемперированная версия гаммы Болена-Пирса состоит из соотношения 3:1, 1902 цента, условно чистой квинты плюс октава (то есть совершенной двенадцатой), называемой в этой теории тритавой ( play ( help · info ) ) и разделить на тринадцать равных частей. Это обеспечивает очень точное соответствие правильно настроенным отношениям, состоящим только из нечетных чисел. Каждый шаг стоит 146,3 цента ( play ( help · info ) ), или 13 √ 3 .
Венди Карлос создала три необычных равных темперамента после тщательного изучения свойств возможных темпераций с размером шага от 30 до 120 центов. Их назвали альфа , бета и гамма . Их можно рассматривать как равные части совершенной квинты. Каждый из них обеспечивает очень хорошую аппроксимацию нескольких интервалов. [32] Размер их шага:
- альфа : 9 √ 3 ⁄ 2 (78,0 центов) Играть ( помощь · информация )
- бета : 11 √ 3 ⁄ 2 (63,8 цента) Играть ( помощь · информация )
- гамма : 20 √ 3 ⁄ 2 (35,1 цента) Играть ( помощь · информация )
Alpha и Beta можно услышать в заглавной песне ее альбома 1986 года Beauty in the Beast .
Пропорции между полутоном и целым тоном
Этот раздел нуждается в дополнительных ссылках для проверки . ( август 2017 г. ) |
В этом разделе полутон и целый тон могут не иметь своих обычных значений 12-EDO, поскольку в нем обсуждается, как они могут быть изменены по-разному от их простых версий для получения желаемых отношений. Пусть количество шагов в полутоне равно s , а количество шагов в тоне равно t .
Существует ровно одно семейство равных темпераций, которое фиксирует полутон на любой правильной части целого тона, сохраняя при этом ноты в правильном порядке (это означает, что, например, до, ре, ми, фа и фа ♯ находятся в восходящем порядке). порядке, если они сохраняют свои обычные отношения с C). То есть привязка q к правильной дроби в соотношении qt = s также определяет уникальное семейство одного равного темперамента и его кратных, которые удовлетворяют этому соотношению.
Например, где k — целое число, 12 k -EDO устанавливает q = 1 ⁄ 2 , а 19 k -EDO устанавливает q = 1 ⁄ 3 . Наименьшие кратные числа в этих семействах (например, 12 и 19 выше) обладают дополнительным свойством, заключающимся в том, что они не имеют нот за пределами квинтового круга . (В общем случае это неверно; в 24-EDO полудиезы и полубемоли не входят в круг квинт, образованный начиная с C.) Крайними случаями являются 5k -EDO, где q = 0 и полутон становится унисоном, а 7 k -EDO, где q = 1, а полутон и тон — один и тот же интервал.
Зная, сколько шагов в полутоне и тоне в этой одинаковой темперации, можно найти число шагов в октаве. Равно темперамент выполнения вышеупомянутых свойств ( в том числе , не имеющие нот вне круга квинт) делит октаву на 7 т - 2 сек шагов, и квинту в 4 т - с шагами. Если есть ноты за пределами квинтового круга, то нужно умножить эти результаты на n , которое является количеством непересекающихся квинтовых кругов, необходимых для создания всех нот (например, два в 24-EDO, шесть в 72-EDO). (Нужно взять небольшой полутон для этой цели: 19-EDO имеет два полутона, один из которых 1 / 3 тона , а другие2 ⁄ 3 .)
Наименьшим из этих семейств является 12 к -ЕДО, и в частности, 12-ЕДО является наименьшим равным темпераментом, обладающим вышеперечисленными свойствами. Кроме того, это также делает полутон ровно половиной целого тона, что является простейшим возможным соотношением. Вот некоторые из причин, по которым 12-EDO стали наиболее часто используемой равной темперацией. (Другая причина заключается в том, что 12-EDO — это наименьшая равномерная темперация, максимально приближенная к гармонии с 5 границами, а следующим по величине является 19-EDO.)
Каждый выбор дроби q для отношения приводит к точно одному равному семейству темпераментов, но обратное неверно: 47-EDO имеет два разных полутона, где один - 1 / 7 тон, а другой - 8 / 9 , которые не являются дополнениями . друг от друга, как в 19-ЕДО ( 1 ⁄ 3 и 2 ⁄ 3 ). Взятие каждого полутона приводит к разному выбору чистой квинты.
Связанные системы настройки
Регулярные диатонические настройки
Диатоническая настройка в двенадцать равных может быть обобщена до любой обычной диатонической настройки, разделяющей октаву как последовательность шагов TTSTTTS (или ее вращение) со всеми T и всеми S одинакового размера, а S меньше, чем Т. В двенадцати равных S является полутоном и составляет ровно половину размера тона T. Когда S уменьшается до нуля, результатом является TTTTT или равномерная темперация с пятью тонами. По мере того, как полутона становятся больше, в конечном итоге все шаги одинаковы. размер, и результат в семи тонах равного темперамента. Эти две конечные точки не включены в обычные диатонические настройки.
Ноты в обычном диатоническом строе связаны вместе циклом из семи темперированных квинт. Двенадцатитоновая система аналогичным образом обобщается на последовательность CDCDDCDCDCDD (или ее вращение) хроматических и диатонических полутонов, соединенных вместе в цикле из двенадцати пятых. В этом случае семь равных получается в пределе, когда размер C стремится к нулю, и пять равных являются пределом, когда D стремится к нулю, в то время как двенадцать равных, конечно, случай C = D.
Некоторые промежуточные размеры тонов и полутонов также могут быть получены в системах равной темперации. Например, если диатонический полутон в два раза больше хроматического полутона, то есть D = 2*C, результат равен девятнадцати с одним шагом для хроматического полутона, двумя шагами для диатонического полутона и тремя шагами для тона и общим числом. шагов 5*T + 2*S = 15 + 4 = 19 шагов. Получившаяся двенадцатитоновая система очень близка к исторически важной 1/3 запятой, означающей один.
Если хроматический полутон составляет две трети размера диатонического полутона, т. е. C = (2/3) * D, результат равен тридцати одному, с двумя шагами для хроматического полутона, тремя шагами для диатонического полутона и пять шагов для тона, где 5 * T + 2 * S = 25 + 6 = 31 шаг. Получившаяся двенадцатитоновая система очень близка к исторически важной 1/4 запятой, означающей один.
Смотрите также
- Просто интонация
- Музыкальная акустика (физика музыки)
- Музыка и математика
- Микротюнер
- Микротональная музыка
- Настройка фортепиано
- Список средних интервалов
- Диатонический и хроматический
- Электронный тюнер
- Музыкальный тюнинг
использованная литература
Цитаты
- ^ a b Sethares сравнивает несколько одинаковых темпераментов на графике с осями, обращенными от осей в первом сравнении равных темпераментов, и идентичных осей второго. (рис. 4.6, стр. 58)
- ^ О'Доннелл, Майкл. «Основы восприятия звука» . Проверено 11 марта 2017 г. .
- ^ История музыкального звука в Европе, стр. 493-511 Герман Гельмгольц, Александр Дж. Эллис об ощущениях тона , Dover Publications, Inc., Нью-Йорк
- ^ Вареши, Г., и Гауэр, К. (2010). Интонация и компенсация ладовых струнных инструментов. Американский журнал физики, 78 (47), 47-55. https://doi.org/10.1119/1.3226563
- ^ б Фриц А. Каттнер . п. 163.
- ^ Фриц А. Каттнер. «Жизнь и творчество принца Чу Цай-Ю: переоценка его вклада в теорию равного темперамента», стр. 200, Этномузыкология , Vol. 19, № 2 (май 1975 г.), стр. 163–206.
- ↑ Кеннет Робинсон: критическое исследование вклада Чу Цай-юй в теорию равного темперамента в китайской музыке . (Sinologica Coloniensia, Bd. 9.) x, 136 стр. Висбаден: Franz Steiner Verlag GmbH, 1980. DM 36. p.vii «Чу-Цайю первый создатель математики «равного темперамента» в любой точке мира.
- ^ a b Робинсон, Кеннет Г. и Джозеф Нидхэм. 1962. "Физика и физическая технология". В книге «Наука и цивилизация в Китае», том. 4: «Физика и физическая технология», Часть 1: «Физика», под редакцией Джозефа Нидхэма. Кембридж: Университетское издательство. п. 221.
- ^ Фриц А. Каттнер. п. 200.
- ↑ Джин Дж. Чо «Значение открытия музыкального равного темперамента в истории культуры», http://en.cnki.com.cn/Article_en/CJFDTOTAL-XHYY201002002.htm . Архивировано 15 марта 2012 г. в Wayback . Машина
- ^ «Количественный ритуал: политическая космология, придворная музыка и точная математика в Китае семнадцатого века Роджер Харт, факультеты истории и азиатских исследований, Техасский университет, Остин» . Uts.cc.utexas.edu. Архивировано из оригинала 05 марта 2012 г. Проверено 20 марта 2012 г. .
- ↑ Наука и цивилизация в Китае, Том IV: 1 (физика), Джозеф Нидхэм, Cambridge University Press, 1962–2004, стр. 220 и далее.
- ↑ The Shorter Science & Civilization in China, сокращение Колином Ронаном оригинального текста Джозефа Нидхэма, стр. 385.
- ^ Лау Хэнсон, Счеты и практическая математика, стр. 389 (на китайском языке劳汉生《珠算与实用数学》 389页)
- ^ Галилей, В. (1584). Il Fronimo... Dialogo sopra l'arte del bene intavolare. Дж. Скотто : Венеция, ff. 80–89.
- ^ "Resound - Коррупция музыки" . Philresound.co.uk. Архивировано из оригинала на 2012-03-24 . Проверено 20 марта 2012 г. .
- ^ Джакомо Горзанис, ок. 1525 – ок. 1575 Intabolatura di liuto. Женева, 1982 г.
- ^ "Спиначино 1507a: Тематический указатель" . Аппалачский государственный университет. Архивировано из оригинала на 2011-07-25 . Проверено 14 июня 2012 г. .
- ^ "Van de Spiegheling der singconst, под редакцией Рудольфа Раша, The Diapason Press" . Diapason.xentonic.org. 30 июня 2009 г. Архивировано из оригинала 17 июля 2011 г. Проверено 20 марта 2012 г. .
- ^ "Лютни, альты, темпераменты" ISBN Марка Линдли 978-0-521-28883-5
- ↑ Андреас Веркмайстер : Музыкальный парадоксальный дискурс, 1707 г.
- ^ Партч, Гарри (1979). Генезис музыки (2-е изд.). Да Капо Пресс. п. 134 . ISBN 0-306-80106-Х.
- ^ Кордье, Серж. «Le tempérament égal à quintes justes» (на французском языке). Ассоциация исследований и развития музыки . Проверено 2 июня 2010 г. .
- ^ Мортон, Дэвид (1980). «Музыка Таиланда», Музыка многих культур , стр.70. Мэй, Элизабет, изд. ISBN 0-520-04778-8 .
- ^ 有关"七平均律"新文献著作的发现[Выводы новой литературы о гепта-равном темпераменте] (на китайском языке). Архивировано из оригинала 27 октября 2007 г.
«Гепта-равный темперамент» в нашей народной музыке всегда был спорным вопросом.
- ^ 七平均律"琐谈--兼及旧式均孔曲笛制作与转调[резюме О «Системе семи равных настроек» ] (на китайском языке). Архивировано из оригинала 30 сентября 2007 г. Проверено 25 июня 2007 г. .
От флейты за две тысячи лет производственного процесса и японских сякухати, оставшихся в производстве династий Суй и Тан, и фактического темперамента, идентификация людей с использованием так называемых «Семи законов» не менее двух тысяч лет истории; и решили, что эта правовая система связана с флейтовым законом.
- ^ Майлз Ли Скиннер (2007). На пути к четвертьтоновому синтаксису: анализ избранных произведений Блэквуда, Хабы, Айвза и Вышнеградского , с. 55. ISBN 9780542998478 .
- ^ Монзо, Джо (2005). «Равный темперамент» . Энциклопедия микротональной теории музыки Tonalsoft . Джо Монзо . Проверено 26 февраля 2019 г.
- ^ "665эдо" . xenoharmonic (микротональная вики). Архивировано из оригинала 18 ноября 2015 г. . Проверено 18 июня 2014 г. .
- ^ "сходящиеся (log2 (3), 10)" . ВольфрамАльфа . Проверено 18 июня 2014 г. .
- ^
- 3:2 и 4:3, 5:4 и 8:5, 6:5 и 5:3 (последовательность A054540 в OEIS )
- 3:2 и 4:3, 5:4 и 8:5 (последовательность A060525 в OEIS )
- 3:2 и 4:3, 5:4 и 8:5, 7:4 и 8:7 (последовательность A060526 в OEIS )
- 3:2 и 4:3, 5:4 и 8:5, 7:4 и 8:7, 16:11 и 11:8 (последовательность A060527 в OEIS )
- 4:3 и 3:2, 5:4 и 8:5, 6:5 и 5:3, 7:4 и 8:7, 16:11 и 11:8, 16:13 и 13:8 (последовательность A060233 в ОИС )
- 3:2 и 4:3, 5:4 и 8:5, 6:5 и 5:3, 9:8 и 16:9, 10:9 и 9:5, 16:15 и 15:8, 45: 32 и 64:45 (последовательность A061920 в OEIS )
- 3:2 и 4:3, 5:4 и 8:5, 6:5 и 5:3, 9:8 и 16:9, 10:9 и 9:5, 16:15 и 15:8, 45: 32 и 64:45, 27:20 и 40:27, 32:27 и 27:16, 81:64 и 128:81, 256:243 и 243:128 (последовательность A061921 в OEIS )
- 5:4 и 8:5 (последовательность A061918 в OEIS )
- 6:5 и 5:3 (последовательность A061919 в OEIS )
- 6:5 и 5:3, 7:5 и 10:7, 7:6 и 12:7 (последовательность A060529 в OEIS )
- 11:8 и 16:11 (последовательность A061416 в OEIS )
- ^ Карлос, Венди. «Три асимметричных деления октавы» . www.wendycarlos.com . ООО Серендип . Проверено 1 сентября 2016 г. .
- ↑ Милн, А., Сетарес, В. А. и Пламондон, Дж., « Изоморфные контроллеры и динамическая настройка: инвариантные аппликатуры в континууме настройки» . Архивировано 9 января 2016 г. в Wayback Machine , Computer Music Journal , зима 2007 г., Vol. 31, № 4, страницы 15-32.
Источники
- Чо, Джин Джинсон. (2003). Открытие музыкального равного темперамента в Китае и Европе в шестнадцатом веке . Льюистон, Нью-Йорк: Эдвин Меллен Пресс .
- Даффин, Росс В. Как равный темперамент разрушил гармонию (и почему вас это должно волновать) . WWNorton & Company, 2007.
- Йоргенсен, Оуэн. Тюнинг . Издательство Мичиганского государственного университета, 1991. ISBN 0-87013-290-3 .
- Сетарес, Уильям А. (2005). Настройка, тембр, спектр, гамма (2-е изд.). Лондон: Springer-Verlag. ISBN 1-85233-797-4.
- Surjodiningrat, W., Sudarjana, PJ, and Susanto, A. (1972) Тональные измерения выдающихся яванских гамеланов в Джокьякарте и Суракарте , издательство Gadjah Mada University Press, Jogjakarta 1972. Цитируется по https://web.archive.org/web/ 20050127000731/http://web.telia.com/~u57011259/pelog_main.htm . Проверено 19 мая 2006 г.
- Стюарт, П.Дж. (2006) «Из галактики в галактику: музыка сфер» [2]
- Храмов, Михаил. «Приближение 5-предельной просто интонации. Компьютерное моделирование MIDI в отрицательных системах равных делений октавы», Материалы международной конференции SIGMAP-2008 [ постоянная мертвая ссылка ] , 26–29 июля 2008 г., Порту , стр. 181–184 , ISBN 978-989-8111-60-9
дальнейшее чтение
- Sensations of Tone — основополагающая работа Германа фон Гельмгольца по акустике и восприятию звука. Особенно Приложение XX: Дополнения переводчика, страницы 430-556, (pdf страницы 451-577)]
внешняя ссылка
- Вики Xenharmonic об EDO и равных темпераментах
- Центр микротональной музыки Фонда Гюйгенса-Фоккера
- А.Орландини: Музыкальная акустика
- «Темперамент» из приложения к циклопедии мистера Чемберса (1753 г.)
- Барбьери, Патрицио. Энгармонические инструменты и музыка, 1470–1900 гг . (2008) Латина, Il Levante Libreria Editrice
- Фрактальная микротональная музыка , Джим Кукула .
- Все существующие цитаты 18 века об И. С. Бахе и темпераменте
- Доминик Экерсли: « Возвращение к Розетте: очень обычный темперамент Баха »
- Хорошо темпераменты, основанные на определении Веркмейстера
- ЛЮБИМЫЕ МОЩНОСТИ ВЕСОВ ПИТЕРА БУЧА _ _ _ _ _ _ _
- Равные темпераменты
- Китайские открытия


![{\ displaystyle r = {\ sqrt [{n}] {p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)

![{\ displaystyle {\ sqrt [{12}] {2}} = 2 ^ {\ frac {1} {12}} \ приблизительно 1,059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)

![{\ displaystyle P_ {n} = P_ {a} \ left ({\ sqrt [{12}] {2}} \ right) ^ {(na)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{\ displaystyle P_ {40} = 440 \ left ({\ sqrt [{12}] {2}} \ right) ^ {(40-49)} \ приблизительно 261,626 \ \ mathrm {Гц}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\ displaystyle P_ {46} = 440 \ left ({\ sqrt [{12}] {2}} \ right) ^ {(46-49)} \ приблизительно 369,994 \ \ mathrm {Гц}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)


