Выпуклый конус

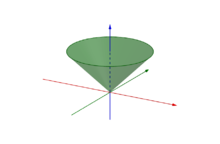
В линейной алгебре , А выпуклый конус является подмножеством из векторного пространства над упорядоченным полем , которое закрыто в соответствии с линейными комбинациями с положительными коэффициентами.

Конус выпуклый (голубой). Внутри него светло-красный выпуклый конус состоит из всех точек αx + βy с α, β> 0 для изображенных x и y . Кривые в правом верхнем углу символизируют бесконечность регионов.

Определение [ править ]

Подмножество С векторного пространства V над упорядоченным полем F является конусом (или иногда называют линейным конусом ) , если для каждого х в С и положительной скалярной & alpha ; в F , продукт αx в C . ^[1] Обратите внимание, что некоторые авторы определяют конус со скаляром α, охватывающим все неотрицательные скаляры (а не все положительные скаляры, которые не включают 0). ^[2]

Конус С является выпуклым конусом , если αx + βy принадлежит C , для любого положительного скаляры & alpha ; , & beta ; , и любого х , у в С . ^{[3] [4]} Конус С выпукла тогда и только тогда , когда С + C ⊆ C .

Эта концепция имеет смысл для любого векторного пространства, которое допускает концепцию «положительного» скаляра, такого как пространства над рациональными , алгебраическими или (чаще) действительными числами . Также отметим , что скаляры в определении положительны что означает , что происхождение не должны принадлежать к С. Некоторые авторы используют определение , что гарантирует происхождение принадлежит C . ^[5] Из-за параметров масштабирования α и β конусы бесконечны по протяженности и не ограничены.

Если C - выпуклый конус, то для любого положительного скаляра α и любого x из C вектор Отсюда следует, что выпуклый конус C является частным случаем линейного конуса .${\ displaystyle \ alpha x = {\ tfrac {\ alpha} {2}} x + {\ tfrac {\ alpha} {2}} x \ in C.}$

Из указанного выше свойства следует, что выпуклый конус можно также определить как линейный конус, замкнутый относительно выпуклых комбинаций или только при сложении . Более кратко, множество C является выпуклым конусом тогда и только тогда, когда αC = C и C + C = C для любого положительного скаляра α .

Примеры [ править ]

Выпуклый конус, не являющийся конической комбинацией конечного числа образующих.

Выпуклый конус, образованный конической комбинацией трех черных векторов.

Конус (объединение двух лучей), который не является выпуклым конусом.

• Для векторного пространства V пустое множество, пространство V и любое линейное подпространство в V являются выпуклыми конусами.
• Коническая комбинация из конечного или бесконечного множества векторов является выпуклым конусом.${\ Displaystyle \ mathbb {R} ^ {п}}$
• В касательные конусы выпуклого множества выпуклые конусы.
• Набор

${\ displaystyle \ left \ {x \ in \ mathbb {R} ^ {2} \ mid x_ {2} \ geq 0, x_ {1} = 0 \ right \} \ cup \ left \ {x \ in \ mathbb {R} ^ {2} \ mid x_ {1} \ geq 0, x_ {2} = 0 \ right \}}$

конус, но не выпуклый конус.

• Конус нормы

${\ displaystyle \ left \ {(x, r) \ in \ mathbb {R} ^ {d + 1} \ mid \ | x \ | \ leq r \ right \}}$

- выпуклый конус.

• Пересечение двух выпуклых конусов в одном векторном пространстве снова является выпуклым конусом, но их объединение может не быть единым.
• Класс выпуклых конусов также замкнут относительно произвольных линейных отображений . В частности, если С является выпуклым конусом, так его противоположность , и является самым большим линейное подпространство содержится в С .${\displaystyle -C}$${\displaystyle C\cap -C}$
• Множество положительно полуопределенных матриц .
• Множество неотрицательных непрерывных функций представляет собой выпуклый конус.

Особые примеры [ править ]

Аффинные выпуклые конусы [ править ]

Аффинный выпуклый конус является множеством полученного в результате применения аффинного преобразования к выпуклому конусу. ^[6] Типичный пример является перевод выпуклого конуса с точкой р : р + С . Технически такие преобразования могут давать неконусы. Например, если p = 0, p + C не является линейным конусом. Однако его до сих пор называют аффинным выпуклым конусом.

Полупространства [ править ]

(Линейная) гиперплоскость - это множество в форме, где f - линейный функционал на векторном пространстве V. Замкнутое полупространство - это множество в форме или, аналогично открытое полупространство, использует строгое неравенство. ^{[7] [8]}${\displaystyle \{x\in V\mid f(x)=c\}}$${\displaystyle \{x\in V\mid f(x)\leq c\}}$${\displaystyle \{x\in V\mid f(x)\geq c\},}$

Полупространства (открытые или замкнутые) - это аффинные выпуклые конусы. Кроме того (в конечных размерах), любой выпуклый конус С , что не все пространством V должен содержаться в некотором замкнутом полупространстве Н от V ; это частный случай леммы Фаркаша .

Многогранные и конечно порожденные конусы [ править ]

Многогранные конусы - это особые виды конусов, которые можно определить несколькими способами: ^{[9] : 256–257}

• Конус C является полиэдральным, если он представляет собой коническую комбинацию конечного числа векторов (это свойство также называется конечно-порожденным ). ^{[10] [11]} Т.е. существует такой набор векторов, что .${\displaystyle \{v_{1},\ldots ,v_{k}\}}$${\displaystyle C=\{a_{1}v_{1}+\cdots +a_{k}v_{k}\mid a_{i}\in \mathbb {R} _{\geq 0},v_{i}\in \mathbb {R} ^{n}\}}$
• Конус является полиэдральным, если он является пересечением конечного числа полупространств, граница которых равна нулю (это было доказано Вейлем в 1935 г.).
• Конус C является полиэдральным, если существует матрица такая, что .${\displaystyle A}$${\displaystyle C=\{x\in \mathbb {R} ^{n}\mid Ax\geq 0\}}$
• Конус является полиэдральным, если он является множеством решений системы однородных линейных неравенств. Алгебраически, каждое неравенство определяется строки матрицы A . Геометрически каждое неравенство определяет полупространство, которое проходит через начало координат.

Каждый конечно порожденный конус является многогранным конусом, а каждый многогранный конус является конечно порожденным конусом. ^[10] Каждый многогранный конус имеет уникальное представление в виде конической оболочки своих экстремальных образующих и уникальное представление пересечений полупространств, учитывая, что каждая линейная форма, связанная с полупространствами, также определяет опорную гиперплоскость грани. ^[12]

Многогранные конусы играют центральную роль в теории представлений многогранников . Например, теорема о разложении для многогранников состояний , что каждый многогранник можно представить в виде суммы Минковского в виде выпуклого многогранника и многогранного конуса. ^{[13] [14]} Многогранные конусы также играют важную роль в доказательстве связанной теоремы о конечном базисе для многогранников, которая показывает, что каждый многогранник является многогранником, а каждый ограниченный многогранник является многогранником. ^{[13] [15] [16]}

Два представления многогранного конуса - неравенствами и векторами - могут иметь очень разные размеры. Например, рассмотрим конус всех неотрицательных п матрицу с размерностью п матриц с равными строк и столбцов сумм. Для представления неравенств требуется n ² неравенств и 2 ( n -1) уравнений, но для векторного представления требуется n ! векторы (см. теорему Биркгофа-фон Неймана ). Может произойти и обратное - количество векторов может быть полиномиальным, а количество неравенств - экспоненциальным. ^{[9] : 256}

Два представления вместе обеспечивают эффективный способ решить, находится ли данный вектор в конусе: чтобы показать, что он находится в конусе, достаточно представить, что это коническая комбинация определяющих векторов; чтобы показать, что его нет в конусе, достаточно указать одно определяющее неравенство, которое оно нарушает. Этот факт известен как лемма Фаркаша .

Тонкий момент в представлении векторами заключается в том, что количество векторов может быть экспоненциальным в размерности, поэтому доказательство того, что вектор находится в конусе, может быть экспоненциально длинным. К счастью, теорема Каратеодори гарантирует, что каждый вектор в конусе может быть представлен не более чем d определяющими векторами, где d - размерность пространства.

Тупые, заостренные, плоские, выступающие и правильные конусы [ править ]

Согласно приведенному выше определению, если C - выпуклый конус, то C ∪ { 0 } также является выпуклым конусом. Выпуклый конус называется острым , если 0 в C , и тупые , если 0 не в C . ^{[1] [17]} Тупые конусы можно исключить из определения выпуклого конуса, заменив «неотрицательный» на «положительный» в условии α, β.

Конус называется плоским, если он содержит некоторый ненулевой вектор x и его противоположный - x, то есть C содержит линейное подпространство размерности не менее единицы, и заметным в противном случае. ^{[18] [19]} Тупой выпуклый конус обязательно заметен, но обратное не обязательно. Выпуклый конус C заметен тогда и только тогда, когда C ∩ - C ⊆ { 0 }. Конус C называется порождающим, если C  -  C равно всему векторному пространству. ^[20]

Некоторые авторы требуют заострения выступающих конусов. ^[21] Термин «заостренный» также часто используется для обозначения замкнутого конуса, который не содержит полной линии (т. Е. Нет нетривиального подпространства объемлющего векторного пространства V или того, что называется выступающим конусом). ^{[22] [23] [24]} Термин собственный ( выпуклый ) конус определяется по-разному, в зависимости от контекста и автора. Это часто означает конус, который удовлетворяет другим свойствам, таким как выпуклый, замкнутый, заостренный, выступающий и полномерный. ^{[25] [26] [27]} Из-за различий в определениях следует обращаться к контексту или источнику для определения этих терминов.

Рациональные конусы [ править ]

Тип конуса, представляющий особый интерес для чистых математиков, - это частично упорядоченный набор рациональных конусов. «Рациональные конусы - важные объекты в торической алгебраической геометрии, комбинаторной коммутативной алгебре, геометрической комбинаторике, целочисленном программировании». ^[28] Этот объект возникает, когда мы изучаем конусы вместе с решеткой . Конус называется рациональным (здесь мы предполагаем «заостренный», как определено выше), если все его образующие имеют целочисленные координаты, т. Е. Если является рациональным конусом, то .${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle \mathbb {Z} ^{d}}$${\displaystyle C}$${\displaystyle C=\{a_{1}v_{1}+\cdots +a_{k}v_{k}\mid a_{i}\in \mathbb {R} _{+},v_{i}\in \mathbb {Z} ^{d}\}}$

Двойной конус [ править ]

Пусть C ⊂ V - множество, не обязательно выпуклое, в вещественном векторном пространстве V, снабженное скалярным произведением . (Непрерывный или топологический) конус, сопряженный с C, - это множество

${\displaystyle C^{*}=\{v\in V\mid \forall w\in C,\langle w,v\rangle \geq 0\},}$

который всегда является выпуклым конусом. Здесь есть двойственность спаривание между C и V , то есть .${\displaystyle \langle w,v\rangle }$${\displaystyle \langle w,v\rangle =v(w)}$

В более общем смысле, (алгебраический) конус, сопряженный с C ⊂ V в линейном пространстве V, является подмножеством двойственного пространства V *, определяемого следующим образом:

${\displaystyle C^{*}:=\left\{v\in V^{*}\mid \forall w\in C,v(w)\geq 0\right\}.}$

Другими словами, если V * есть алгебраическое сопряженное пространство из V , то есть множество линейных функционалов, неотрицательных на прямой конус C . Если мы возьмем V * быть непрерывным сопряженное пространство , то это множество непрерывных линейных функционалов неотрицательных на С . ^[29] Это понятие не требует спецификации внутреннего продукта на V .

В конечных измерениях два понятия двойственного конуса по существу одинаковы, потому что каждый конечномерный линейный функционал является непрерывным ^[30], и каждый непрерывный линейный функционал во внутреннем пространстве произведения индуцирует линейный изоморфизм (невырожденное линейное отображение) от V * к V , и этот изоморфизм переводит двойственный конус, заданный вторым определением, в V * , на конус, заданный первым определением; см. теорему Рисса о представлении . ^[29]

Если C совпадает со своим двойственным конусом, то C называется самодуальным . Можно сказать, что конус самодвойственный без ссылки на любой заданный внутренний продукт, если существует внутренний продукт, по отношению к которому он равен своему двойственному по первому определению.

Конструкции [ править ]

• Учитывая , замкнутое, выпуклое подмножество К из гильбертова пространства V , то наружу нормальный конус к множеству К в точке х в K задается

${\displaystyle N_{K}(x)=\left\{p\in V\;:\;\forall x^{*}\in K,\langle p,x^{*}-x\rangle \leq 0\right\}.}$

• Учитывая замкнутое выпуклое подмножество K в V , касательный конус (или условный конус ) к множеству K в точке x задается формулой

${\displaystyle T_{K}(x)={\overline {\bigcup _{h>0}{\tfrac {1}{h}}(K-x)}}.}$

• Учитывая замкнутое выпуклое подмножество K гильбертова пространства V , касательный конус к множеству K в точке x в K можно определить как полярный конус к внешнему нормальному конусу :${\displaystyle N_{K}(x)}$

${\displaystyle T_{K}(x)=N_{K}^{*}(x){\overset {\underset {\mathrm {def} }{}}{=}}\{y\in V|\forall \xi \in N_{K}(x):\langle y,\xi \rangle \leqslant 0\}}$

И нормальный, и касательный конус имеют свойство быть замкнутым и выпуклым. Это важные концепции в области выпуклой оптимизации , вариационных неравенств и проектируемых динамических систем .

Свойства [ править ]

Если C - непустой выпуклый конус в X , то линейная оболочка C равна C - C, а наибольшее векторное подпространство X, содержащееся в C , равно C ∩ (- C ). ^[31]

Частичный порядок, определяемый выпуклым конусом [ править ]

Заостренный и выступающий выпуклый конус C индуцирует частичный порядок "≤" на V , определенный так, что тогда и только тогда (если конус плоский, то же определение дает просто предварительный порядок .) Суммы и положительные скалярные кратные действительных неравенств относительно в этом порядке остаются в силе неравенства. Векторное пространство с таким порядком называется упорядоченным векторным пространством . Примеры включают порядок произведения на вещественнозначных векторах и порядок Лёвнера для положительных полуопределенных матриц. Такой порядок обычно встречается в позитивном полуопределенном программировании.${\displaystyle x\leq y}$${\displaystyle y-x\in C.}$${\displaystyle \mathbb {R} ^{n},}$

См. Также [ править ]

• Конус (значения)
  • Конус (геометрия)
  • Конус (топология)
  • Конус (линейная алгебра)
• Лемма Фаркаша
• Биполярная теорема
• Линейная комбинация
• Упорядоченное векторное пространство

Заметки [ править ]

Ссылки [ править ]

• Бурбаки, Николас (1987). Топологические векторные пространства . Элементы математики. Берлин, Нью-Йорк: Springer-Verlag . ISBN 978-3-540-13627-9.
• Наричи, Лоуренс ; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC  144216834 .
• Рокафеллар, RT (1997) [1970]. Выпуклый анализ . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 1-4008-7317-7.
• Шефер, Гельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . GTM . 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Трев, Франсуа (2006) [1967]. Топологические векторные пространства, распределения и ядра . Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-45352-1. OCLC  853623322 .
• Зэлинеску, К. (2002). Выпуклый анализ в общих векторных пространствах . Ривер Эдж, штат Нью-Джерси: World Scientific. ISBN 981-238-067-1. Руководство по ремонту  1921556 .