Бинарная тетраэдрическая группа

Правильный комплексный многогранник 3 {6} 2 или или же , представляет диаграмму Кэли для бинарной тетраэдрической группы, где каждый красный и синий треугольник является направленным подграфом. ^[1]

В математике , то бинарная группа тетраэдра , обозначается 2T или ⟨2,3,3⟩ определенная неабелева группа из порядка 24. Это расширение из группы тетраэдра Т или (2,3,3) 12 - го порядка с помощью циклического группы порядка 2 и является прообразом группы тетраэдра при покрывающем гомоморфизме 2: 1 Spin (3) → SO (3) специальной ортогональной группы по спиновой группе . Отсюда следует, что бинарная группа тетраэдра является дискретной подгруппой Spin (3) порядка 24. Комплексная группа отражений, названная 3 (24) 3 по формулеGC Shephard или 3 [3] 3 ипо Кокстеру , изоморфна бинарной тетраэдрической группе.

Бинарную группу тетраэдров проще всего описать конкретно как дискретную подгруппу единичных кватернионов при изоморфизме Spin (3) ≅ Sp (1) , где Sp (1) - мультипликативная группа единичных кватернионов. (Описание этого гомоморфизма см. В статье о кватернионах и пространственных поворотах .)

Элементы [ править ]

Граф Кэли SL (2,3)

Проекции симметрии

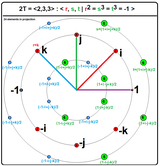8-кратный	12-кратный
24 элемента кватерниона: 1 заказ-1: 1 1 заказ-2: -1 6-й порядок-4: ± i, ± j, ± k 8 порядок-6: (+ 1 ± i ± j ± k) / 2 8 порядок-3: (-1 ± i ± j ± k) / 2.

Явно, бинарная тетраэдрическая группа получают в качестве группы единиц в кольце от Гурвицы целых чисел . Всего таких единиц 24

${\ displaystyle \ {\ pm 1, \ pm i, \ pm j, \ pm k, {\ tfrac {1} {2}} (\ pm 1 \ pm i \ pm j \ pm k) \}}$

со всеми возможными комбинациями знаков.

Все 24 единицы имеют абсолютное значение 1 и, следовательно, принадлежат к кватернионной группе единиц Sp (1). Выпуклая оболочка этих 24 элементов в 4-мерном пространстве образует выпуклую обычный 4-многогранник называется 24-клетка .

Свойства [ править ]

Бинарная тетраэдрическая группа, обозначенная 2T, вписывается в короткую точную последовательность

${\ displaystyle 1 \ to \ {\ pm 1 \} \ to 2 \ mathrm {T} \ to \ mathrm {T} \ to 1.}$

Эта последовательность не расщепляется , что означает, что 2T не является полупрямым произведением {± 1} на T. На самом деле не существует подгруппы 2T, изоморфной T.

Бинарная тетраэдральная группа - это накрывающая группа тетраэдрической группы. Если рассматривать группу тетраэдра как знакопеременную группу из четырех букв, T ≅ A ₄ , мы, таким образом, имеем бинарную группу тетраэдра как покрывающую группу, 2T ≅ .${\displaystyle {\widehat {\mathrm {A} _{4}}}}$

Центр 2Т является подгруппа {± 1}. Группа внутренних автоморфизмов изоморфна A ₄ , а полная группа автоморфизмов изоморфна S ₄ . ^[2]

Бинарная тетраэдральная группа может быть записана как полупрямое произведение

${\displaystyle 2\mathrm {T} =\mathrm {Q} \rtimes \mathrm {C} _{3}}$

где Q - группа кватернионов, состоящая из 8 липшицевых единиц, а C ₃ - циклическая группа порядка 3, порожденная ω = -1/2(1 + я + j + k ) . Группа Z ₃ действует на нормальную подгруппу Q сопряжением . Сопряжение с помощью ω - это автоморфизм Q, который циклически вращает i , j и k .

Можно показать, что бинарная группа тетраэдра изоморфна специальной линейной группе SL (2,3) - группе всех матриц 2 × 2 над конечным полем F ₃ с единичным детерминантом, причем этот изоморфизм покрывает изоморфизм проективного специального линейная группа PSL (2,3) с знакопеременной группой A ₄ .

Презентация [ править ]

У группы 2T есть презентация, проведенная

${\displaystyle \langle r,s,t\mid r^{2}=s^{3}=t^{3}=rst\rangle }$

или, что эквивалентно,

${\displaystyle \langle s,t\mid (st)^{2}=s^{3}=t^{3}\rangle .}$

Генераторы с этими отношениями даются

${\displaystyle r=k\qquad s={\tfrac {1}{2}}(1+i+j+k)\qquad t={\tfrac {1}{2}}(1+i+j-k),}$

с .${\displaystyle r^{2}=s^{3}=t^{3}=-1}$

Подгруппы [ править ]

Группа кватернионов, состоящая из 8 липшицевых единиц, образует нормальную подгруппу в 2T индекса 3. Эта группа и центр {± 1} являются единственными нетривиальными нормальными подгруппами.

Все остальные подгруппы в 2T являются циклическими группами, порожденными различными элементами порядков 3, 4 и 6. ^[3]

Высшие измерения [ править ]

Подобно тому , как тетраэдрические группы обобщаются на вращательную симметрии группы п - симплекс (как подгруппы SO ( п )), есть соответствующая выше двоичная группа, 2-кратное покрытие, исходя из крышки Spin ( п ) → SO ( n ).

Группу вращательной симметрии n -симплекса можно рассматривать как знакопеременную группу на n  + 1 точках, A _{n +1} , а соответствующая бинарная группа является 2-кратной накрывающей группой . Для всех высших размерностей, кроме A ₆ и A ₇ (соответствующих 5-мерным и 6-мерным симплексам), эта бинарная группа является покрывающей группой (максимальное покрытие) и является суперсовершенной , но для размерностей 5 и 6 есть дополнительные исключительные 3-кратное покрытие, и бинарные группы не являются суперсовершенными.

Использование в теоретической физике [ править ]

Бинарная тетраэдрическая группа была использована в контексте теории Янга – Миллса в 1956 году Чен Нин Яном и другими. ^[4] Впервые он был использован при построении модели физики ароматов Полом Фрэмптоном и Томасом Кефартом в 1994 году. ^[5] В 2012 году было показано ^[6], что связь между двумя углами смешивания нейтрино, полученная ^[7] с использованием этого бинарного тетраэдра симметрия аромата, согласуется с экспериментом.

См. Также [ править ]

• Бинарная полиэдральная группа
• двоичная циклическая группа , ⟨ п ⟩, порядок 2 н
• бинарная группа диэдра , ⟨2,2, п ⟩, порядок 4 н
• бинарная октаэдрическая группа , 2O = ⟨2,3,4⟩, порядок 48
• бинарная группа икосаэдра , 2I = ⟨2,3,5⟩, порядок 120

Заметки [ править ]

Ссылки [ править ]

• Конвей, Джон Х .; Смит, Дерек А. (2003). О кватернионах и октонионах . Натик, Массачусетс: AK Peters, Ltd. ISBN 1-56881-134-9.
• Кокстер, HSM и Мозер, WOJ (1980). Генераторы и отношения для дискретных групп, 4-е издание . Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9.6.5. Бинарные группы полиэдров, с. 68