Кантор набор

В математике , то множество Кантора представляет собой совокупность точек , лежащих на одном сегменте линии , которая имеет целый ряд замечательных и глубоких свойств. Он был открыт в 1874 году Генри Джоном Стивеном Смитом ^{[1] [2] [3] [4]} и представлен немецким математиком Георгом Кантором в 1883 году. ^{[5] [6]}

Рассмотрев этот набор, Кантор и другие помогли заложить основы современной топологии наборов точек . Хотя сам Кантор определил набор в общем абстрактном виде, наиболее распространенной современной конструкцией является тройной набор Кантора , построенный путем удаления средней трети линейного сегмента и последующего повторения процесса с оставшимися более короткими сегментами. Сам Кантор упомянул тернарную конструкцию лишь мимоходом, как пример более общей идеи о совершенном множестве , которое нигде не плотно .

Увеличьте набор Кантора. Каждая точка в наборе представлена ​​здесь вертикальной линией.

Построение и формула троичного множества [ править ]

Тройной набор Кантора создается путем итеративного удаления открытой средней трети из набора линейных сегментов. Начинают с удаления открытой средней трети (${\ Displaystyle {\ mathcal {C}}}$1/3, 2/3) из интервала [0, 1], оставив два отрезка: [0, 1/3] ∪ [2/3, 1]. Затем открытая средняя треть каждого из этих оставшихся сегментов удаляется, оставляя четыре линейных сегмента: [0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1]. Этот процесс продолжается до бесконечности , где n- й набор

${\ displaystyle C_ {n} = {\ frac {C_ {n-1}} {3}} \ cup \ left ({\ frac {2} {3}} + {\ frac {C_ {n-1}}) {3}} \ right) {\ text {for}} n \ geq 1, {\ text {и}} C_ {0} = [0,1].}$

Тройное множество Кантора содержит все точки в интервале [0, 1], которые не удаляются ни на каком этапе этого бесконечного процесса:

${\ displaystyle {\ mathcal {C}}: = \ bigcap _ {n = 1} ^ {\ infty} C_ {n}.}$

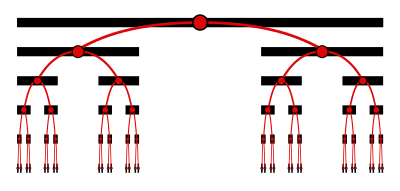
Первые шесть шагов этого процесса показаны ниже.

Используя идею автомодельных преобразований и явные замкнутые формулы для множества Кантора ^[7]${\displaystyle T_{L}(x)=x/3,T_{R}(x)=(2+x)/3}$${\displaystyle C_{n}=T_{L}(C_{n-1})\cup T_{R}(C_{n-1}),}$

${\displaystyle {\mathcal {C}}=[0,1]\smallsetminus \bigcup _{n=0}^{\infty }\bigcup _{k=0}^{3^{n}-1}\left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right),}$

где каждая средняя треть удалена как открытый интервал из окружающего его замкнутого интервала , или${\displaystyle \textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$${\displaystyle \textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[{\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\right]}$

${\displaystyle {\mathcal {C}}=\bigcap _{n=1}^{\infty }\bigcup _{k=0}^{3^{n-1}-1}\left(\left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\right),}$

где средняя треть предыдущего отрезка удалена путем пересечения с${\displaystyle \textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$${\displaystyle \textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[{\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]}$${\displaystyle \textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right].}$

Этот процесс удаления средних третей - простой пример правила конечного подразделения . Тройное множество Кантора представляет собой пример фрактальной струны .

В арифметических терминах множество Кантора состоит из всех действительных чисел единичного интервала, которым не требуется цифра 1 для выражения троичной дроби (с основанием 3). Как показано на приведенной выше диаграмме, каждая точка в наборе Кантора уникально расположена на пути через бесконечно глубокое двоичное дерево, где путь поворачивается влево или вправо на каждом уровне в зависимости от того, на какой стороне удаленного сегмента находится точка. Представление каждого поворота влево с помощью 0 и каждого поворота вправо с помощью 2 дает троичную дробь для точки.${\displaystyle [0,1]}$

Состав [ править ]

Поскольку набор Кантора определяется как набор не исключенных точек, пропорция (т. Е. Мера ) оставшегося единичного интервала может быть найдена по общей удаленной длине. Эта сумма представляет собой геометрическую прогрессию.

${\displaystyle \sum _{n=0}^{\infty }{\frac {2^{n}}{3^{n+1}}}={\frac {1}{3}}+{\frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\left({\frac {1}{1-{\frac {2}{3}}}}\right)=1.}$

Так что оставшаяся пропорция 1 - 1 = 0.

Этот расчет предполагает, что множество Кантора не может содержать интервал ненулевой длины. Может показаться удивительным, что что-то должно остаться - ведь сумма длин удаленных интервалов равна длине исходного интервала. Однако более пристальный взгляд на процесс показывает, что что-то должно быть оставлено, поскольку удаление «средней трети» каждого интервала связано с удалением открытых наборов (наборов, которые не включают их конечные точки). Итак, удаление отрезка (1/3, 2/3) из исходного интервала [0, 1] оставляет после себя точки 1/3 и 2/3. Последующие шаги не удаляют эти (или другие) конечные точки, поскольку удаленные интервалы всегда являются внутренними по отношению к оставшимся интервалам. Таким образом, множество Кантора не является пустым и фактически содержит несчетное бесконечное количество точек (как следует из приведенного выше описания в терминах путей в бесконечном двоичном дереве).

Может показаться, что остались только концы строительных сегментов, но это тоже не так. Номер1/4, например, имеет уникальную троичную форму 0,020202 ... = 0,02 . Он находится в нижней трети, и в верхней трети этой трети, и в нижней трети этой верхней трети, и так далее. Поскольку он никогда не находится в одном из средних сегментов, он никогда не удаляется. Тем не менее, он также не является конечной точкой какого-либо среднего сегмента, потому что он не кратен какой-либо степени 1/3. ^[8] Все конечные точки сегментов являются завершающими троичными дробями и содержатся в наборе

${\displaystyle \{x\in [0,1]\mid \exists i\in \mathbb {N} _{0}:x\,3^{i}\in \mathbb {Z} \}\qquad {\Bigl (}\subset \mathbb {N} _{0}\,3^{-\mathbb {N} _{0}}{\Bigr )}}$

которое является счетно бесконечным множеством. Что касается мощности , почти все элементы множества Кантора не являются конечными точками интервалов, и все множество Кантора не счетно.

Свойства [ править ]

Мощность [ править ]

Можно показать, что в этом процессе осталось столько же точек, сколько было вначале, и, следовательно, множество Кантора несчетно . Чтобы убедиться в этом, мы покажем , что существует функция F из множества Кантора на отрезке [0,1], сюръективны (т.е. ф отображений на [0,1]) , так что мощность из не менее , чем из [0,1]. Поскольку является подмножеством [0,1], его мощность также не больше, поэтому две мощности должны быть фактически равны по теореме Кантора – Бернштейна – Шредера .${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Чтобы построить эту функцию, рассмотрите точки в интервале [0, 1] в терминах системы счисления с основанием 3 (или троичной ). Напомним, что правильные троичные дроби, точнее: элементы , допускают более одного представления в этой записи, например${\displaystyle {\bigl (}\mathbb {Z} \smallsetminus \{0\}{\bigr )}\cdot 3^{-\mathbb {N} _{0}}}$1/3, которое можно записать как 0,1 ₃ = 0,1 0 ₃ , но также как 0,0222 ... ₃ = 0,0 2 ₃ , и2/3, которое можно записать как 0,2 ₃ = 0,2 0 _3, но также как 0,1222 ... ₃ = 0,1 2 ₃ . ^[9] Когда мы удаляем среднюю треть, она содержит числа с троичными цифрами вида 0,1xxxxx ... _3, где xxxxx ... ₃ находится строго между 00000 ... ₃ и 22222 ... ₃ . Итак, числа, оставшиеся после первого шага, состоят из

• Числа вида 0,0ххххх ... ₃ (включая 0,022222 ... ₃ = 1/3)
• Числа вида 0,2ххххх ... ₃ (включая 0,222222 ... ₃ = 1)

Это можно резюмировать, сказав, что числа с троичным представлением, в которых первая цифра после точки счисления не равна 1, являются числами , остающимися после первого шага.

На втором этапе удаляются числа вида 0,01хххх ... ₃ и 0,21хххх ... ₃ , и (с должным вниманием к конечным точкам) можно сделать вывод, что оставшиеся числа являются числами с троичными числами, где ни одно из первых две цифры - 1.

Продолжая таким образом, чтобы число не было исключено на шаге n , оно должно иметь троичное представление, n- я цифра которого не равна 1. Чтобы число было в наборе Кантора, оно не должно исключаться ни на каком шаге, оно должен допускать числовое представление, целиком состоящее из нулей и двоек.

Стоит подчеркнуть, что числа вроде 1, 1/3= 0,1 ₃ и7/9= 0,21 ₃ входят в набор Кантора, поскольку они имеют троичные числа, состоящие полностью из нулей и двоек: 1 = 0,222 ... ₃ = 0, 2 ₃ ,1/3= 0,0222 ... ₃ = 0,0 2 ₃ и7/9= 0,20222 ... ₃ = 0,20 2 ₃ . Все последние номера «конечные точки», и эти примеры правильные предельные точки из . То же верно и для левых предельных точек , например${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$2/3= 0,1222 ... ₃ = 0,1 2 ₃ = 0,2 0 ₃ и8/9= 0,21222 ... ₃ = 0,21 2 ₃ = 0,22 0 ₃ . Все эти конечные точки являются собственными троичными дробями (элементами ) вида${\displaystyle \mathbb {Z} \cdot 3^{-\mathbb {N} _{0}}}$п/q, где знаменатель q представляет собой степень 3, когда дробь находится в своей неприводимой форме. ^[8] Тернарное представление этих дробей обрывается (т. Е. Конечно) или - напомним, что каждая собственная троичная дробь имеет 2 представления - бесконечно и «заканчивается» либо бесконечным количеством повторяющихся нулей, либо бесконечным числом повторяющихся двоек. Такая фракция является левым предельной точкой в случае его троичное представление не содержит 1 - х и «концов» в бесконечно многих повторяющихся 0s. Точно так же правильная тернарная дробь является правой предельной точкой, если снова ее троичное разложение не содержит единиц и «оканчивается» на бесконечном количестве повторяющихся двоек.${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Этот набор конечных точек плотен в (но не плотен в [0, 1]) и составляет счетно бесконечное множество. Числа, в которых не являются конечными точками, также имеют только 0 и 2 в их троичном представлении, но они не могут заканчиваться бесконечным повторением цифры 0 или цифры 2, потому что тогда это будет конечная точка.${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Функция от до [0,1] определяется путем взятия троичных чисел, которые полностью состоят из 0 и 2, замены всех 2 на 1 и интерпретации последовательности как двоичного представления действительного числа. В формуле${\displaystyle {\mathcal {C}}}$

${\displaystyle f{\bigg (}\sum _{k\in \mathbb {N} }a_{k}3^{-k}{\bigg )}=\sum _{k\in \mathbb {N} }{\frac {a_{k}}{2}}2^{-k}}$   куда   ${\displaystyle \forall k\in \mathbb {N} :a_{k}\in \{0,2\}.}$

Для любого числа y в [0,1] его двоичное представление может быть преобразовано в троичное представление числа x in путем замены всех единиц на 2. При этом, е ( х ) = у , так что у находится в диапазоне от F . Например, если y = ³ ⁄ ₅ = 0,100110011001 ... ₂ = 0. 1001 , мы пишем x = 0. 2002 = 0,200220022002 ... ₃ = ⁷ ⁄ ₁₀ . Следовательно, f${\displaystyle {\mathcal {C}}}$сюръективно. Однако f не является инъективным - значения, для которых f ( x ) совпадает, находятся на противоположных концах одной из удаленных средних третей . Например, возьмите

¹ ⁄ ₃ = 0,0 2 ₃ (что является правой граничной точкой и левой граничной точкой средней трети [ ¹ ⁄ ₃ , ² ⁄ ₃ ]) и${\displaystyle {\mathcal {C}}}$

² ⁄ ₃ = 0,2 0 ₃ (что является левой и правой граничной точкой средней трети [ ¹ ⁄ ₃ , ² ⁄ ₃ ])${\displaystyle {\mathcal {C}}}$

так

${\displaystyle {\begin{array}{lcl}f{\bigl (}{}^{1}\!\!/\!_{3}{\bigr )}=f(0.0{\overline {2}}_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0}}_{2}=f(0.2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr )}.\\&\parallel \\&{}^{1}\!\!/\!_{2}\end{array}}}$

Таким образом, в канторовом множестве столько точек, сколько их в интервале [0, 1] (который имеет несчетную мощность ). Однако набор конечных точек удаленных интервалов является счетным, поэтому в наборе Кантора должно быть несчетное количество чисел, которые не являются конечными точками интервала. Как отмечалось выше, одним из примеров такого числа является ¹ ⁄ ₄ , что может быть записано как 0,020202 ... ₃ = 0,02 в троичной системе счисления. На самом деле, учитывая любые , существуют такие, что . Впервые это было продемонстрировано Штейнхаусом в 1917 году, который доказал с помощью геометрического аргумента эквивалентное утверждение, что для каждого .${\displaystyle {\mathfrak {c}}=2^{\aleph _{0}}}$${\displaystyle a\in [-1,1]}$${\displaystyle x,y\in {\mathcal {C}}}$${\displaystyle a=y-x}$${\displaystyle \{(x,y)\in \mathbb {R} ^{2}\,|\,y=x+a\}\;\cap \;({\mathcal {C}}\times {\mathcal {C}})\neq \emptyset }$${\displaystyle a\in [-1,1]}$^[10] Поскольку эта конструкция обеспечивает инъекцию изв, мы имеемв качестве немедленного следствия. Предполагаячтодля любого бесконечного множества(выписка показано, что эквивалентно аксиоме выбора по Тарского ), это дает еще одну демонстрацию этого.${\displaystyle [-1,1]}$${\displaystyle {\mathcal {C}}\times {\mathcal {C}}}$${\displaystyle |{\mathcal {C}}\times {\mathcal {C}}|\geq |[-1,1]|={\mathfrak {c}}}$${\displaystyle |A\times A|=|A|}$${\displaystyle A}$${\displaystyle |{\mathcal {C}}|={\mathfrak {c}}}$

Множество Кантора содержит столько точек, сколько интервал, из которого оно взято, но само по себе не содержит интервалов ненулевой длины. У иррациональных чисел есть то же свойство, но у множества Кантора есть дополнительное свойство замкнутости, поэтому оно даже не является плотным в любом интервале, в отличие от иррациональных чисел, которые плотны в каждом интервале.

Было высказано предположение, что все алгебраические иррациональные числа нормальны . Поскольку члены множества Кантора не являются нормальными, это означало бы, что все члены множества Кантора либо рациональны, либо трансцендентны .

Самоподобие [ править ]

Набор Кантора - прототип фрактала . Он самоподобен , потому что равен двум копиям самого себя, если каждая копия будет уменьшена в 3 раза и переведена. Точнее, множество Кантора равно объединению двух функций, левого и правого преобразований самоподобия и , которые оставляют множество Кантора инвариантным с точностью до гомеоморфизма :${\displaystyle T_{L}(x)=x/3}$${\displaystyle T_{R}(x)=(2+x)/3}$${\displaystyle T_{L}({\mathcal {C}})\cong T_{R}({\mathcal {C}})\cong {\mathcal {C}}=T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}}).}$

Повторные итерация из и можно представить в виде бесконечного двоичного дерева . То есть в каждом узле дерева можно рассматривать поддерево слева или справа. Взятие множества вместе с функциональной композицией образует моноид , диадический моноид .${\displaystyle T_{L}}$${\displaystyle T_{R}}$${\displaystyle \{T_{L},T_{R}\}}$

В автоморфизмах бинарного дерева являются его гиперболическими вращениями, и задаются модулярной группой . Таким образом, множество Кантора является однородным пространством в том смысле, что для любых двух точек и множества Кантора существует гомеоморфизм с . Явное построение может быть описано проще, если мы будем рассматривать множество Кантора как пространство произведения счетного числа копий дискретного пространства . Тогда отображение, определяемое с помощью, является инволютивным гомеоморфизмом, меняющим местами и .${\displaystyle x}$${\displaystyle y}$${\displaystyle {\mathcal {C}}}$${\displaystyle h:{\mathcal {C}}\to {\mathcal {C}}}$${\displaystyle h(x)=y}$${\displaystyle h}$${\displaystyle \{0,1\}}$${\displaystyle h:\{0,1\}^{\mathbb {N} }\to \{0,1\}^{\mathbb {N} }}$${\displaystyle h_{n}(u):=u_{n}+x_{n}+y_{n}\mod 2}$${\displaystyle x}$${\displaystyle y}$

Закон о сохранении [ править ]

Было обнаружено, что за масштабирование и самоподобие всегда отвечает некоторая форма закона сохранения. В случае множества Кантора можно видеть, что момент th (где - фрактальная размерность) всех уцелевших интервалов на любом этапе процесса построения равен константе, которая равна единице в случае множества Кантора ^{[11 ] [12]} . Мы знаем, что существуют интервалы размера, присутствующие в системе на этапе ее построения. Тогда, если мы обозначим оставшиеся интервалы как, то наступит момент с .${\displaystyle d_{f}}$${\displaystyle d_{f}=\ln(2)/\ln(3)}$${\displaystyle N=2^{n}}$${\displaystyle 1/3^{n}}$${\displaystyle n}$${\displaystyle x_{1},x_{2},\ldots ,x_{2^{n}}}$${\displaystyle d_{f}}$${\displaystyle x_{1}^{d_{f}}+x_{2}^{d_{f}}+\cdots +x_{2^{n}}^{d_{f}}=1}$${\displaystyle x_{1}=x_{2}=\cdots =x_{2^{n}}=1/3^{n}}$

Размерность Хаусдорфа множества Cantor равно Ln (2) / Ln (3) ≈ 0,631.

Топологические и аналитические свойства [ править ]

Хотя «набор Кантора» обычно относится к исходному кантору в средней трети, описанному выше, топологи часто говорят о «канторовском множестве», что означает любое топологическое пространство, гомеоморфное ему (топологически эквивалентное).

Как показывают приведенные выше суммирования аргументов показывает, что множество Кантора несчетно , но имеет меру Лебега 0. Так как множество Кантора является дополнением к союзу с открытых множеств , оно само по себе является замкнутым подмножеством действительных чисел, и , следовательно, полное метрическое пространство . Поскольку он также вполне ограничен , теорема Гейне – Бореля утверждает, что он должен быть компактным .

Для любой точки в канторовом множестве и любой сколь угодно малой окрестности точки существует какое-то другое число с троичными числами, состоящими только из нулей и двоек, а также числа, троичные цифры которых содержат единицы. Следовательно, каждая точка в наборе Кантора является точкой накопления (также называемой точкой кластера или предельной точкой) набора Кантора, но ни одна из них не является внутренней точкой . Замкнутое множество, в котором каждая точка является точкой накопления, также называется совершенным множеством в топологии , в то время как замкнутое подмножество интервала без внутренних точек нигде не является плотным в интервале.

Каждая точка множества Кантора также является точкой накопления дополнения множества Кантора.

Для любых двух точек в наборе Кантора будет некоторая троичная цифра, где они различаются - одна будет иметь 0, а другая 2. Разделив набор Кантора на «половинки» в зависимости от значения этой цифры, можно получить разделение набор Кантора в два закрытых набора, которые разделяют исходные две точки. В относительной топологии на множестве Кантора точки были разделены закрытым множеством . Следовательно, множество Кантора полностью отключено . Как компактное полностью несвязное хаусдорфово пространство , множество Кантора является примером пространства Стоуна .

В качестве топологического пространства , множество Кантора, естественно гомеоморфно к продукту из счетного числа экземпляров пространства , где каждый экземпляр несет дискретную топологию . Это пространство всех последовательностей в две цифры ${\displaystyle \{0,1\}}$

${\displaystyle 2^{\mathbb {N} }=\{(x_{n})\mid x_{n}\in \{0,1\}{\text{ for }}n\in \mathbb {N} \}}$,

которое также можно отождествить с набором 2-адических чисел . Основой для открытых множеств топологии произведения являются цилиндровыми комплектами ; гомеоморфизм отображает их в топологию подпространства, которую множество Кантора наследует от естественной топологии на прямой действительных чисел. Эта характеризация пространства Кантора как продукта компактных пространств дает второе доказательство компактности пространства Кантора с помощью теоремы Тихонова .

Из приведенной выше характеризации канторово множество гомеоморфно p-адическим целым числам и, если из него удалить одну точку, p-адическим числам .

Множество Кантора - это подмножество вещественных чисел, которые представляют собой метрическое пространство по отношению к обычной метрике расстояния ; поэтому само множество Кантора является метрическим пространством с использованием той же самой метрики. В качестве альтернативы можно использовать p-адическую метрику для : заданных двух последовательностей , расстояние между ними равно , где - наименьший индекс такой, что ; если такого индекса нет, то две последовательности совпадают, и одна определяет расстояние равным нулю. Эти две метрики создают одинаковую топологию на множестве Кантора.${\displaystyle 2^{\mathbb {N} }}$${\displaystyle (x_{n}),(y_{n})\in 2^{\mathbb {N} }}$${\displaystyle d((x_{n}),(y_{n}))=2^{-k}}$${\displaystyle k}$${\displaystyle x_{k}\neq y_{k}}$

Выше мы видели, что канторово множество является полностью несвязным совершенным компактным метрическим пространством. В самом деле, в некотором смысле оно единственное: всякое непустое вполне несвязное совершенное компактное метрическое пространство гомеоморфно канторову множеству. См. Пространство Кантора для получения дополнительной информации о пространствах, гомеоморфных множеству Кантора.

Множество Кантора иногда рассматривается как «универсальный» в категории от компактных метрических пространств , так как любое компактное метрическое пространство является непрерывным образом множества Кантора; однако эта конструкция не уникальна, и поэтому множество Кантора не универсально в точном категориальном смысле. Свойство «универсальности» имеет важные приложения в функциональном анализе , где его иногда называют теоремой представления для компактных метрических пространств . ^[13]

Для любого целого q ≥ 2 топология на группе G = Z _q ^ω (счетная прямая сумма) дискретна. Хотя двойственный по Понтрягину Γ также является Z _q ^ω , топология Γ компактна. Видно, что Γ полностью несвязна и совершенна, а значит, гомеоморфна канторову множеству. Гомеоморфизм проще всего выписать явно в случае q = 2. (См. Рудин 1962, стр. 40.)

Геометрическое среднее из множества Cantor приблизительно 0,274974. ^{[14] [ ненадежный источник? ]}

Мера и вероятность [ править ]

Множество Кантора можно рассматривать как компактную группу двоичных последовательностей, и, как таковое, оно наделено естественной мерой Хаара . При нормализации таким образом, чтобы мера набора была равна 1, это модель бесконечной последовательности подбрасываний монеты. Более того, можно показать, что обычная мера Лебега на интервале является образом меры Хаара на канторовом множестве, в то время как естественная инъекция в троичное множество является каноническим примером особой меры . Также можно показать, что мера Хаара является образом любой вероятности , что в некотором смысле делает канторовское множество универсальным вероятностным пространством.

В теории меры Лебега канторово множество является примером несчетного множества, имеющего нулевую меру. ^[15]

Числа Кантора [ править ]

Если мы определим число Кантора как член множества Кантора, то ^[16]

• (1) Каждое действительное число в [0, 2] является суммой двух чисел Кантора.
• (2) Между любыми двумя числами Кантора стоит число, не являющееся числом Кантора.

Теория описательных множеств [ править ]

Множество Кантора - это скудный набор (или набор первой категории) как подмножество [0,1] (хотя и не как подмножество самого себя, поскольку это пространство Бэра ). Таким образом, множество Кантора демонстрирует, что понятия «размер» с точки зрения мощности, меры и категории (Бэра) могут не совпадать. Подобно множеству , множество Кантора «маленькое» в том смысле, что это нулевое множество (множество с нулевой мерой), и это скудное подмножество [0,1]. Однако, в отличие от счетного и имеющего «малую» мощность, мощность у такой же, как у [0,1], континуум${\displaystyle \mathbb {Q} \cap [0,1]}$${\displaystyle {\mathcal {C}}}$${\displaystyle \mathbb {Q} \cap [0,1]}$${\displaystyle \aleph _{0}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathfrak {c}}}$, и является «большим» в смысле мощности. Фактически, также возможно построить подмножество [0,1], которое является скудным, но с положительной мерой, и подмножество, которое не является скудным, но с нулевой мерой: ^[17] Взяв счетное объединение «толстого» Кантора множества мер (конструкция см. ниже в наборе Смита – Вольтерра – Кантора), мы получаем набор, который имеет положительную меру (равную 1), но скуден на [0,1], поскольку каждое из них нигде не плотно. Тогда рассмотрим набор . Поскольку , не может быть скудным, но поскольку , должно иметь нулевую меру.${\displaystyle {\mathcal {C}}^{(n)}}$${\displaystyle \lambda =(n-1)/n}$${\displaystyle {\mathcal {A}}:=\bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$${\displaystyle {\mathcal {C}}^{(n)}}$${\displaystyle {\mathcal {A}}^{\mathrm {c} }=[0,1]\setminus \bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$${\displaystyle {\mathcal {A}}\cup {\mathcal {A}}^{\mathrm {c} }=[0,1]}$${\displaystyle {\mathcal {A}}^{\mathrm {c} }}$${\displaystyle \mu ({\mathcal {A}})=1}$${\displaystyle {\mathcal {A}}^{\mathrm {c} }}$

Варианты [ править ]

Набор Смита – Вольтерры – Кантора [ править ]

Вместо того, чтобы многократно удалять среднюю треть каждой части, как в наборе Кантора, мы могли бы также удалить любой другой фиксированный процент (кроме 0% и 100%) из середины. В случае удаления средних ⁸ ⁄ ₁₀ интервала мы получаем замечательно доступный случай - набор состоит из всех чисел в [0,1], которые могут быть записаны как десятичная дробь, состоящая полностью из 0 и 9. Если фиксированный процент удаляется на каждом этапе, то ограничивающий набор будет иметь нулевую меру, поскольку длина остатка такая же, как для любого f, такого, что .${\displaystyle (1-f)^{n}\to 0}$${\displaystyle n\to \infty }$${\displaystyle 0<f\leq 1}$

С другой стороны, «толстые канторовские множества» положительной меры могут быть сгенерированы путем удаления более мелких частей середины сегмента на каждой итерации. Таким образом, можно построить множества, гомеоморфные множеству Кантора, которые имеют положительную меру Лебега, но нигде не плотны. Если интервал длины ( ) удаляется с середины каждого сегмента на п - й итерации, то общая длина удаляемого , и предельное множество будет иметь меру Лебега о . Таким образом, в некотором смысле канторовское множество средних третей является предельным случаем с . Если , то остаток будет иметь положительную меру . Случай известен как множество Смита – Вольтерра – Кантора.${\displaystyle r^{n}}$${\displaystyle r\leq 1/3}$${\textstyle \sum _{n=1}^{\infty }2^{n-1}r^{n}=r/(1-2r)}$${\displaystyle \lambda =(1-3r)/(1-2r)}$${\displaystyle r=1/3}$${\displaystyle 0<r<1/3}$${\displaystyle 0<\lambda <1}$${\displaystyle r=1/4}$, имеющий меру Лебега .${\displaystyle 1/2}$

Стохастический набор Кантора [ править ]

Можно изменить конструкцию множества Кантора путем случайного деления, а не поровну. Кроме того, чтобы включить время, мы можем разделить только один из доступных интервалов на каждом шаге вместо того, чтобы делить все доступные интервалы. В случае стохастического триадического множества Кантора результирующий процесс может быть описан следующим уравнением скорости ^{[11] [12]}

${\displaystyle {{\partial c(x,t)} \over {\partial t}}=-{{x^{2}} \over {2}}c(x,t)+2\int _{x}^{\infty }(y-x)c(y,t)\,dy,}$

и для стохастического диадического множества Кантора ^[18]

${\displaystyle {{\partial c(x,t)} \over {\partial t}}=-xc(x,t)+(1+p)\int _{x}^{\infty }c(y,t)\,dy,}$

где - количество интервалов размера между и . В случае триадного множества Кантора фрактальная размерность меньше, чем его детерминированный аналог . В случае стохастического диадического множества Кантора фрактальная размерность снова меньше, чем у его детерминированного аналога . В случае стохастического диадического множества Кантора решение для демонстрирует динамическое масштабирование, поскольку его решение в пределе большого времени - это фрактальная размерность стохастического диадического множества Кантора . В любом случае, как и в триадическом канторовом множестве, момент -й ( ) стохастического триадического и диадического канторовского множества также являются сохраняющимися величинами.${\displaystyle c(x,t)dx}$${\displaystyle x}$${\displaystyle x+dx}$${\displaystyle 0.5616}$${\displaystyle 0.6309}$${\displaystyle p}$${\displaystyle \ln(1+p)/\ln 2}$${\displaystyle c(x,t)}$${\displaystyle t^{-(1+d_{f})}e^{-xt}}$${\displaystyle d_{f}=p}$${\displaystyle d_{f}}$${\displaystyle \int x^{d_{f}}c(x,t)dx={\text{constant}}}$

Канторская пыль [ править ]

Пыль Кантора - это многомерная версия множества Кантора. Его можно сформировать, взяв на себя конечное декартово произведение канторовского множества, сделав его канторовым пространством . Как и набор Кантора, пыль Кантора имеет нулевую меру . ^[19]

Другой 2D-аналог набора Кантора - ковер Серпинского , где квадрат разделен на девять меньших квадратов, а средний удален. Затем оставшиеся квадраты делятся на девять, а середина удаляется, и так до бесконечности. ^[20] Одним из трехмерных аналогов этого является губка Менгера .

Кристофер Домас представил интерактивный инструмент бинарной визуализации на основе канторской пыли на Black Hat USA 2012. ^[21]

Исторические заметки [ править ]

Сам Кантор определил множество в общем, абстрактном смысле и упомянул троичную конструкцию лишь мимоходом, как пример более общей идеи - идеального множества , которое нигде не плотно . В оригинальной статье представлено несколько различных конструкций абстрактной концепции.

Этот набор считался абстрактным в то время, когда его изобрел Кантор. Сам Кантор пришел к этому из-за практических соображений по поводу набора точек, в которых тригонометрический ряд может не сходиться. Это открытие во многом поставило его на путь развития абстрактной общей теории бесконечных множеств .

См. Также [ править ]

• Множество Смита – Вольтерры – Кантора
• Гексаграммы (И Цзин)
• Функция Кантора
• Куб Кантора
• Ожерелье Антуана
• Коха снежинка
• Фан Кнастера – Куратовского
• Список фракталов по размерности Хаусдорфа
• Последовательность Мозера – де Брейна

Примечания [ править ]

Ссылки [ править ]

Внешние ссылки [ править ]

• «Набор Кантора» , Энциклопедия математики , EMS Press , 2001 [1994]
• Cantor Наборы и Кантор набор и функции в вырез на-узел
• Сет Кантора в Платонических мирах