Эллиптические функции Якоби

В математике эллиптические функции Якоби представляют собой набор основных эллиптических функций . Они встречаются при описании движения маятника (см. также маятник (математика) ), а также при конструировании электронных эллиптических фильтров . В то время как тригонометрические функции определяются со ссылкой на окружность, эллиптические функции Якоби являются обобщением, которое относится к другим коническим сечениям , в частности к эллипсу. Связь с тригонометрическими функциями содержится в обозначениях, например, с помощью обозначения соответствия для${\ Displaystyle \ имя_оператора {SN}}$${\ Displaystyle \ грех}$. Эллиптические функции Якоби чаще используются в практических задачах, чем эллиптические функции Вейерштрасса, поскольку они не требуют определения и/или понимания понятий комплексного анализа. Их ввел Карл Густав Якоб Якоби  ( 1829 ). Карл Фридрих Гаусс еще в 1797 г. изучал специальные эллиптические функции Якоби, в частности лемнискатные эллиптические функции ^[1] , но его работа была опубликована намного позже.

Есть двенадцать эллиптических функций Якоби, обозначаемых , где и любые буквы , , , и . (Функции формы тривиально устанавливаются равными единице для полноты обозначений.) - аргумент и параметр, оба из которых могут быть сложными.${\displaystyle \operatorname {pq} (u,m)}$${\displaystyle \mathrm {p} }$${\displaystyle \mathrm {q} }$${\displaystyle \mathrm {c} }$${\displaystyle \mathrm {s} }$${\displaystyle \mathrm {n} }$${\displaystyle \mathrm {d} }$${\displaystyle \operatorname {pp} (u,m)}$${\displaystyle u}$${\displaystyle m}$

Основной прямоугольник на комплексной плоскости${\displaystyle u}$

Эллиптическая функция Якоби${\displaystyle \operatorname {cn} }$

Эллиптическая функция Якоби${\displaystyle \operatorname {dn} }$

Эллиптическая функция Якоби${\displaystyle \operatorname {sc} }$

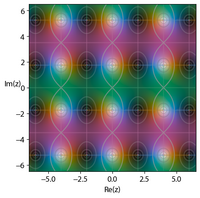
Графики четырех эллиптических функций Якоби в комплексной плоскости , иллюстрирующие их двойное периодическое поведение. Изображения, созданные с использованием версии метода доменной окраски . ^[3] Все значения равны .${\displaystyle u}$${\displaystyle k={\sqrt {m}}}$${\displaystyle 0.8}$

Модель амплитуды Якоби (измеренной по вертикальной оси) как функции независимых переменных u и модуля k

График эллипса Якоби ( x ² + y ² /b ² =1, b real) и двенадцати эллиптических функций Якоби pq(u,m) для конкретных значений угла φ и параметра b . Сплошная кривая — эллипс с m = 1-1/b ² и u = F(φ,m), где F(.,.) — эллиптический интеграл первого рода (с параметром ). Пунктирная кривая — единичная окружность. Касательные линии от окружности и эллипса в точке x=cd, пересекающие ось x в точке dc, показаны светло-серым цветом.${\displaystyle m=k^{2}}$

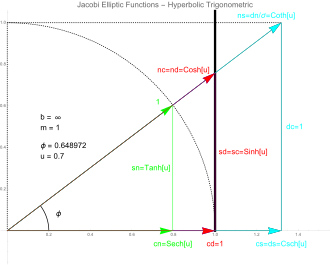
График вырожденной кривой Якоби ( x ²  +  y ² / b ²  = 1, b  = ∞) и двенадцати эллиптических функций Якоби pq( u ,1) для конкретного значения угла  φ . Сплошная кривая — вырожденный эллипс ( x ²  = 1) с m  = 1 и u  =  F ( φ , 1), где F (·, \middot') — эллиптический интеграл первого рода. Пунктирная кривая — единичная окружность. Поскольку это функции Якоби для m = 0 (круговые тригонометрические функции), но с мнимыми аргументами они соответствуют шести гиперболическим тригонометрическим функциям.

График гиперболы Якоби ( x ²  +  y ² / b ²  = 1, b мнимое) и двенадцати эллиптических функций Якоби pq( u , m ) для конкретных значений угла φ и параметра b . Сплошная кривая — это гипербола с m  = 1 − 1/ b ² и u  =  F ( φ , m ), где F (·, ·) — эллиптический интеграл первого рода. Пунктирная кривая — единичная окружность. Для треугольника ds-dc σ = sin( φ )cos( φ ).

Графики фазы для двенадцати эллиптических функций Якоби pq(u,m) как комплексного аргумента функции u с указанием полюсов и нулей. Графики представляют собой один полный цикл в реальном и мнимом направлениях, а цветная часть указывает фазу в соответствии с цветовым кругом в правом нижнем углу (который заменяет тривиальную функцию dd). Области с абсолютным значением ниже 1/3 окрашены в черный цвет, что примерно указывает на расположение нуля, а области с абсолютным значением выше 3 окрашены в белый цвет, что примерно указывает на положение полюса. На всех графиках используется m  = 2/3 с K  =  K ( m ), K ′ =  K (1 -  m ), K(·) — полный эллиптический интеграл первого рода. Стрелки на полюсах указывают направление нулевой фазы. Стрелки вправо и влево означают положительные и отрицательные вещественные остатки соответственно. Стрелки вверх и вниз означают положительные и отрицательные мнимые остатки соответственно.