Лемнискатные эллиптические функции

В математике лемнискатные эллиптические функции — это эллиптические функции , связанные с длиной дуги лемнискаты Бернулли . Впервые они были изучены Джулио Фагнано в 1718 году, а затем , среди прочих , Леонардом Эйлером и Карлом Фридрихом Гауссом .

Лемнискатные функции синуса и лемнискатного косинуса , обычно записываемые символами sl и cl (иногда вместо них используются символы sinlem и coslem или sin lemn и cos lemn ) ^[1] , аналогичны тригонометрическим функциям синуса и косинуса. В то время как тригонометрический синус связывает длину дуги с длиной хорды в круге единичного диаметра , синус лемнискаты связывает длину дуги с длиной хорды лемнискаты. ${\ Displaystyle х ^ {2} + у ^ {2} = х}$${\ displaystyle {\ bigl (} x ^ {2} + y ^ {2} {\ bigr)} {} ^ {2} = x ^ {2} -y ^ {2}.}$

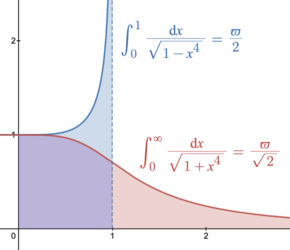
Функции лемнискаты имеют периоды, связанные с числом 2,622057... называемым константой лемнискаты , отношением периметра лемнискаты к ее диаметру.${\ Displaystyle \ варпи =}$

Функции sl и cl имеют квадратную решетку периодов (кратную целым числам Гаусса ) с фундаментальными периодами ^[2] и являются частным случаем двух эллиптических функций Якоби на этой решетке, .${\ Displaystyle \ {(1 + я) \ варпи, (1-я) \ варпи \},}$${\ displaystyle \ operatorname {sl} z = \ operatorname {sn} (z; i),}$ ${\ displaystyle \ operatorname {cl} z = \ operatorname {cd} (z; i)}$

Точно так же гиперболические лемнискатные функции slh и clh имеют квадратную решетку периодов с фундаментальными периодами${\ displaystyle {\ bigl \ {} {\ sqrt {2}} \ varpi, {\ sqrt {2}} \ varpi i {\ bigr \}}.}$

Лемнискатные функции и гиперболические лемнискатные функции связаны с эллиптической функцией Вейерштрасса .${\ Displaystyle \ wp (г; а, 0)}$

Лемнискатный синус (красный) и лемнискатный косинус (фиолетовый) применяются к вещественному аргументу по сравнению с тригонометрическим синусом y = sin( πx / ϖ ) (бледно-красный).

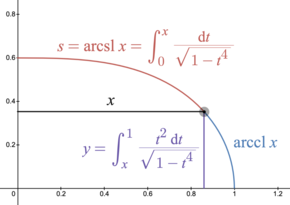
Синус и косинус лемнискаты связывают длину дуги дуги лемнискаты с расстоянием одной конечной точки от начала координат.

Тригонометрические синус и косинус аналогично связывают длину дуги дуги окружности единичного диаметра с расстоянием одной конечной точки от начала координат.

Синус лемнискаты связывает длину дуги с координатой x в прямоугольной эластике.

${\ displaystyle \ operatorname {sl} z}$в комплексной плоскости. ^[10] На рисунке видно, что фундаментальные периоды и являются «минимальными» в том смысле, что они имеют наименьшее абсолютное значение из всех периодов, действительная часть которых неотрицательна.${\ Displaystyle (1 + я) \ варпи}$${\ Displaystyle (1-я) \ varpi}$

Геометрическое представление и${\ Displaystyle \ варпи / 2}$${\ Displaystyle \ varpi / {\ sqrt {2}}}$

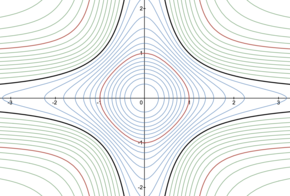
Кривые x ² ​​⊕ y ² = a для различных значений a . Отрицательный a в зеленом, положительный a в синем, a = ± 1 в красном, a = ∞ в черном.

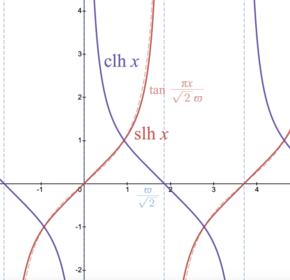
Гиперболический лемнискатный синус (красный) и гиперболический лемнискатный косинус (фиолетовый) применяются к вещественному аргументу по сравнению с тригонометрическим тангенсом (бледно-красный).

По отношению к кривой Ферма четвертой степени гиперболический лемнискатный синус аналогичен тригонометрической функции тангенса.${\ Displaystyle х ^ {4} + у ^ {4} = 1}$

«Мир в пятиконечной проекции» Пирса (1879 г.).