В геометрии два или более объекта называются концентрическими , соосными или соосными, если они имеют один и тот же центр или ось . Круги , [1] правильные многоугольники [2] и правильные многогранники , [3] и сферы [4] могут быть концентричными друг другу (с одной центральной точкой), как и цилиндры [5] (с одной центральной осью).
Геометрические свойства [ править ]
В евклидовой плоскости две концентрические окружности обязательно имеют разные радиусы друг от друга. [6] Однако круги в трехмерном пространстве могут быть концентрическими и иметь одинаковый радиус друг с другом, но, тем не менее, быть разными кругами. Например, два разных меридиана земного шара концентричны друг другу и земному шару (аппроксимированы сферой). В более общем смысле, каждые два больших круга на сфере концентричны друг другу и со сферой. [7]
По теореме Эйлера в геометрии о расстоянии между центром описанной окружности и центром треугольника две концентрические окружности (с нулевым расстоянием) являются описанной и вписанной окружностью треугольника тогда и только тогда, когда радиус одной из них в два раза больше радиуса другой. , в этом случае треугольник равносторонний . [8] : с. 198
Описанная и вписанная окружности правильного n -угольника и сам правильный n -угольник концентрически. Отношение окружного радиуса к внутреннему радиусу для различных n см. В разделе Двухцентровый многоугольник # Правильные многоугольники . То же самое можно сказать и о регулярном многограннике «s insphere , midsphere и circumsphere .
Область плоскости между двумя концентрическими кругами представляет собой кольцо , и аналогично область пространства между двумя концентрическими сферами представляет собой сферическую оболочку . [4]
Для данной точки c на плоскости множество всех окружностей с центром c образует пучок окружностей . Каждые два круга в карандаше концентрические и имеют разные радиусы. Каждая точка на плоскости, кроме общего центра, принадлежит ровно одной из окружностей карандаша. Каждые две непересекающиеся окружности и каждый гиперболический пучок окружностей можно преобразовать в набор концентрических окружностей преобразованием Мёбиуса . [9] [10]
Приложения и примеры [ править ]
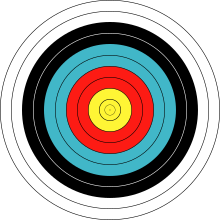
В ряби , образованная путем сбрасывания небольшого объекта в стоячую воду , естественно , образует расширяющуюся систему концентрических окружностей. [11] Равномерно расположенные круги на мишенях, используемых в стрельбе из лука [12] или аналогичных видах спорта, являются еще одним знакомым примером концентрических кругов.
Коаксиальный кабель - это тип электрического кабеля, в котором объединенная нейтраль и жила заземления полностью окружают токоведущую жилу (сердечники) в системе концентрических цилиндрических оболочек. [13]
Johannes Kepler «s Тайна мироздания предполагал космологическую систему , образованную концентрической правильных многогранников и сфер. [14]
Концентрические круги также встречаются в диоптрийных прицелах , типе механических прицелов, которые обычно встречаются на винтовках-мишенях. Обычно они имеют большой диск с отверстием малого диаметра возле глаза стрелка и мушку (круг внутри другого круга, называемый туннелем ). Когда эти прицелы правильно выровнены, точка попадания будет в середине круга мушки.
См. Также [ править ]
- Число центрированного куба
- Гомеоид
- Фокалоид
- Круговая симметрия
- Магический круг (математика)
- Спираль
Ссылки [ править ]
- ^ Александр, Дэниел С .; Коберлейн, Гералин М. (2009), Элементарная геометрия для студентов колледжей , Cengage Learning, стр. 279, ISBN 9781111788599.
- ^ Харди, Годфри Гарольд (1908), Курс чистой математики , The University Press, стр. 107.
- ^ Гиллард, Роберт Д. (1987), Всесторонняя координационная химия: теория и предпосылки , Pergamon Press, стр.137, 139 , ISBN 9780080262321.
- ^ a b Апостол, Том (2013), Новые горизонты в геометрии , Dolciani Mathematical Expositions, 47 , Mathematical Association of America, стр. 140, ISBN 9780883853542.
- ^ Сперк, Джозеф; Аксель, Нури (2008), Механика жидкости , Springer, стр. 174, ISBN 9783540735366.
- ^ Коул, Джордж М .; Харбин, Эндрю Л. (2009), Справочное руководство геодезиста , www.ppi2pass.com, §2, стр. 6, ISBN 9781591261742.
- ^ Морс, Джедидия (1812), Американская универсальная география ;: или, Взгляд на нынешнее состояние всех королевств, штатов и колоний в известном мире, Том 1 (6-е изд.), Томас и Эндрюс, стр. 19.
- ^ Драгутин Свртан и Дарко Вельян (2012), «Неевклидовы версии некоторых классических неравенств треугольника» , forumgeom.fau.edu , Forum Geometricorum, стр. 197–209
- Перейти ↑ Hahn, Liang-shin (1994), Комплексные числа и геометрия , MAA Spectrum, Cambridge University Press, стр. 142, ISBN 9780883855102.
- ^ Браннан, Дэвид А .; Эсплен, Мэтью Ф .; Грей, Джереми Дж. (2011), Геометрия , Cambridge University Press, стр. 320–321, ISBN 9781139503709.
- ^ Флеминг, сэр Джон Амброуз (1902), Волны и рябь в воде, воздухе и эфире: курс рождественских лекций, читаемых в Королевском институте Великобритании , Общество содействия христианскому знанию, стр. 20.
- ^ Хейвуд, Кэтлин; Льюис, Кэтрин (2006), Стрельба из лука: шаги к успеху , Human Kinetics, стр. xxiii, ISBN 9780736055420.
- ^ Вейк, Мартин (1997), Стандартный словарь по волоконной оптике , Springer, стр. 124, ISBN 9780412122415.
- ^ Мейер, Уолтер А. (2006), Геометрия и ее приложения (2-е изд.), Academic Press, стр. 436, ISBN 9780080478036.
Внешние ссылки [ править ]
- Геометрия: демонстрация концентрических кругов с интерактивной анимацией
