Дисперсия (волны на воде)

В динамике жидкости , дисперсия из воды волн обычно относится к частотной дисперсии , что означает , что волны разных длин волн , движутся с разными скоростями фазы . Водные волны в этом контексте - это волны, распространяющиеся по поверхности воды , с гравитацией и поверхностным натяжением в качестве восстанавливающих сил . В результате вода со свободной поверхностью обычно считается диспергирующей средой .

Для определенной глубины воды поверхностные гравитационные волны - т.е. волны, возникающие на границе раздела воздух-вода и гравитация как единственная сила, восстанавливающая плоскостность, - распространяются быстрее с увеличением длины волны . С другой стороны, для данной (фиксированной) длины волны гравитационные волны в более глубокой воде имеют большую фазовую скорость, чем в более мелкой воде . ^[1] В отличие от гравитационных волн, капиллярные волны (т. Е. Вызванные только поверхностным натяжением) распространяются быстрее для более коротких длин волн.

Помимо частотной дисперсии, волны на воде также обладают дисперсией амплитуды. Это нелинейный эффект, из-за которого волны большей амплитуды имеют отличную фазовую скорость от волн малой амплитуды.

Частотная дисперсия поверхностных гравитационных волн [ править ]

Этот раздел посвящен частотной дисперсии волн в слое жидкости под действием силы тяжести и в соответствии с линейной теорией. О влиянии поверхностного натяжения на частотную дисперсию см. Эффекты поверхностного натяжения в теории волн Эйри и капиллярных волнах .

Распространение и дисперсия волн [ править ]

Синусоидальная волна.

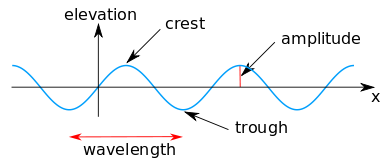
Простейшая распространяющаяся волна неизменной формы - это синусоида . Синусоидальная волна с возвышением водной поверхности η (x, t) определяется выражением ^[2]

${\ Displaystyle \ эта (х, т) = а \ грех \ влево (\ тета (х, т) \ вправо), \,}$

где a - амплитуда (в метрах), а θ = θ (x, t) - функция фазы (в радианах ), зависящая от горизонтального положения (  x  , в метрах) и времени (  t  , в секундах ): ^[3]

${\ displaystyle \ theta = 2 \ pi \ left ({\ frac {x} {\ lambda}} - {\ frac {t} {T}} \ right) = kx- \ omega t,}$   с     и   ${\ Displaystyle к = {\ гидроразрыва {2 \ pi} {\ lambda}}}$${\ displaystyle \ omega = {\ frac {2 \ pi} {T}},}$

куда:

• λ - длина волны (в метрах),
• T - период (в секундах),
• k - волновое число (в радианах на метр) и
• ω - угловая частота (в радианах в секунду).

Характерные фазы водной волны:

• пересечение нуля снизу вверх при θ = 0 ,
• гребень волны при θ =  ½  π ,
• переход через нуль вниз при θ = π и
• впадина волны при θ = 1½ π .

Определенная фаза повторяется после целого числа m, кратного 2π : sin ( θ ) = sin ( θ + m • 2π ).

Существенным для волн на воде и других волновых явлений в физике является то, что свободно распространяющиеся волны ненулевой амплитуды существуют только тогда, когда угловая частота ω и волновое число k (или, что эквивалентно, длина волны λ и период T ) удовлетворяют функциональному соотношению : частотная дисперсия соотношение ^{[4] [5]}

${\ Displaystyle \ omega ^ {2} = \ Omega ^ {2} (к). \,}$

У дисперсионного соотношения есть два решения: ω = + Ω (k) и ω = −Ω (k) , соответствующие волнам, распространяющимся в положительном или отрицательном направлении x . В общем случае дисперсионное соотношение будет зависеть от нескольких других параметров в дополнение к волновому числу k . Для гравитационных волн, согласно линейной теории, это ускорение свободного падения g и глубина воды h . Дисперсионное соотношение для этих волн: ^{[6] [5]}

неявное уравнение с TANH обозначая гиперболический тангенс функцию.

Начальная фаза волны θ = θ ₀ распространяется как функция пространства и времени . Его последующее положение определяется следующим образом:

${\displaystyle x={\frac {\lambda }{T}}\,t+{\frac {\lambda }{2\pi }}\,\theta _{0}={\frac {\omega }{k}}\,t+{\frac {\theta _{0}}{k}}.}$

Это показывает, что фаза движется со скоростью: ^[2]

${\displaystyle c_{p}={\frac {\lambda }{T}}={\frac {\omega }{k}}={\frac {\Omega (k)}{k}},}$

которая называется фазовой скоростью.

Фазовая скорость [ править ]

Синусоидальной волны, малой поверхности подъема амплитуды и с постоянной длиной волны , распростран с фазовой скоростью , которая также называется Celerity или скорость фазы. Хотя фазовая скорость является вектором и имеет соответствующее направление, скорость или фазовая скорость относятся только к величине фазовой скорости. Согласно линейной теории волн, вызванных силой тяжести, фазовая скорость зависит от длины волны и глубины воды. При фиксированной глубине воды длинные волны (с большой длиной волны) распространяются быстрее, чем более короткие волны.

На левом рисунке видно, что волны на мелководье с длинами волн λ, намного превышающими глубину воды h , распространяются с фазовой скоростью ^[2]

${\displaystyle c_{p}={\sqrt {gh}}\qquad \scriptstyle {\text{(shallow water),}}\,}$

где g - ускорение силы тяжести, а c _p - фазовая скорость. Поскольку эта фазовая скорость мелкой воды не зависит от длины волны, волны на мелкой воде не имеют частотной дисперсии.

Используя другую нормализацию для того же соотношения частотной дисперсии, рисунок справа показывает, что для фиксированной длины волны λ фазовая скорость c _p увеличивается с увеличением глубины воды. ^[1] До тех пор, пока в глубокой воде с глубиной воды h больше половины длины волны λ (так, при h / λ> 0,5 ) фазовая скорость c _p не зависит от глубины воды: ^[2]

${\displaystyle c_{p}={\sqrt {\frac {g\lambda }{2\pi }}}={\frac {g}{2\pi }}T\qquad \scriptstyle {\text{(deep water),}}}$

с Т волна период ( обратный от частоты F , Т = 1 / F ). Итак, на большой глубине фазовая скорость увеличивается с длиной волны и периодом.

Поскольку фазовая скорость удовлетворяет условию c _p  = λ / T = λf , длина волны и период (или частота) связаны. Например, в глубокой воде:

${\displaystyle \lambda ={\frac {g}{2\pi }}T^{2}\qquad \scriptstyle {\text{(deep water).}}}$

Ниже приведены дисперсионные характеристики для промежуточной глубины.

Групповая скорость [ править ]

Интерференция двух синусоидальных волн с немного разными длинами волн, но с одинаковой амплитудой и направлением распространения, приводит к форме биений , называемой группой волн. Как видно на анимации, группа движется с групповой скоростью c _g, отличной от фазовой скорости c _p , из-за частотной дисперсии.

Групповая скорость изображена красными линиями (отмеченными буквой B ) на двух рисунках выше. На мелководье групповая скорость равна фазовой скорости мелководья. Это связано с тем, что волны на мелководье не имеют дисперсии. На большой глубине групповая скорость равна половине фазовой скорости: c _g  = ½ c _p . ^[7]

Групповая скорость также оказывается скоростью переноса энергии. Это скорость, с которой средняя волновая энергия переносится горизонтально в узкополосном волновом поле. ^{[8] [9]}

В случае, если групповая скорость отличается от фазовой скорости, следствием этого является то, что количество волн, подсчитываемых в группе волн, отличается при подсчете по снимку в космосе в определенный момент от количества волн, отсчитываемых по времени от измеренной отметки поверхности. в фиксированном положении. Рассмотрим группу волн длиной Λ _g и длительностью группы τ _g . Групповая скорость: ^[10]

${\displaystyle c_{g}={\frac {\Lambda _{g}}{\tau _{g}}}.}$

Количество волн в группе волн, измеренное в пространстве в определенный момент, равно: Λ _g  / λ . В то время как измерена в фиксированном месте во время, число волн в группе: τ _г  / Т . Таким образом, отношение количества волн, измеренных в пространстве, к количеству волн, измеренных во времени, составляет:

${\displaystyle {\tfrac {\text{No. of waves in space}}{\text{No. of waves in time}}}={\frac {\Lambda _{g}/\lambda }{\tau _{g}/T}}={\frac {\Lambda _{g}}{\tau _{g}}}\cdot {\frac {T}{\lambda }}={\frac {c_{g}}{c_{p}}}.}$

Итак, на глубокой воде, с c _g = ½ c _p , ^[11] группа волн имеет в два раза больше волн во времени, чем в пространстве. ^[12]

Высота поверхности воды η (x, t) как функция горизонтального положения x и времени t для двухцветной волновой группы с полной модуляцией может быть математически сформулирована как: ^[11]

${\displaystyle \eta =a\,\sin \left(k_{1}x-\omega _{1}t\right)+a\,\sin \left(k_{2}x-\omega _{2}t\right),}$

с:

• а амплитуда волны каждой частотной составляющей в метрах,
• K ₁ и K ₂ на волновое число каждого компонента волны, в радианах на метр, и
• ω ₁ и ω ₂ - угловая частота каждой составляющей волны в радианах в секунду.

Как ω _{1, так} и k ₁ , а также ω ₂ и k ₂ должны удовлетворять дисперсионному соотношению:

${\displaystyle \omega _{1}^{2}=\Omega ^{2}(k_{1})\,}$   и   ${\displaystyle \omega _{2}^{2}=\Omega ^{2}(k_{2}).\,}$

Используя тригонометрические тождества , отметка поверхности записывается как: ^[10]

${\displaystyle \eta =\left[2\,a\,\cos \left({\frac {k_{1}-k_{2}}{2}}x-{\frac {\omega _{1}-\omega _{2}}{2}}t\right)\right]\;\cdot \;\sin \left({\frac {k_{1}+k_{2}}{2}}x-{\frac {\omega _{1}+\omega _{2}}{2}}t\right).}$

Часть в квадратных скобках - это медленно меняющаяся амплитуда группы с групповым волновым числом ½ (k ₁  - k ₂  ) и групповой угловой частотой ½ (ω ₁  - ω ₂  ) . В результате групповая скорость для предела k ₁  → k ₂  : ^{[10] [11]}

${\displaystyle c_{g}=\lim _{k_{1}\,\to \,k_{2}}{\frac {\omega _{1}-\omega _{2}}{k_{1}-k_{2}}}=\lim _{k_{1}\,\to \,k_{2}}{\frac {\Omega (k_{1})-\Omega (k_{2})}{k_{1}-k_{2}}}={\frac {{\text{d}}\Omega (k)}{{\text{d}}k}}.}$

Группы волн можно различить только в случае узкополосного сигнала, при этом разница волновых чисел k ₁  - k ₂ мала по сравнению со средним волновым числом ½ (k ₁  + k ₂ ) .

Многокомпонентные волновые паттерны [ править ]

Эффект частотной дисперсии заключается в том, что волны распространяются как функция длины волны, так что пространственные и временные фазовые свойства распространяющейся волны постоянно меняются. Например, под действием силы тяжести волны на воде с большей длиной волны распространяются быстрее, чем волны с меньшей длиной волны.

В то время как две наложенные синусоидальные волны, называемые бихроматической волной, имеют огибающую, которая распространяется без изменений, три или более синусоидальных волновых составляющих приводят к изменению структуры волн и их огибающей. Состояние моря, то есть настоящие волны на море или в океане, можно описать как суперпозицию множества синусоидальных волн с разными длинами волн, амплитудами, начальными фазами и направлениями распространения. Каждый из этих компонентов движется со своей фазовой скоростью в соответствии с дисперсионным соотношением. В статистике такой поверхности можно описать его спектра мощности . ^[13]

Отношение дисперсии [ править ]

В приведенной ниже таблице дано дисперсионное соотношение ω ² = [ Ω (k) ] ² между угловой частотой ω = 2π / T и волновым числом k = 2π / λ , а также фазовая и групповая скорости. ^[10]

Частотная дисперсия гравитационных волн на поверхности глубокой воды, мелководья и на промежуточных глубинах согласно теории линейных волн
количество	символ	единицы	глубокая вода ( h > ½ λ )	мелководье ( h <0,05 λ )	промежуточная глубина (все λ и h )
соотношение дисперсии	${\displaystyle \displaystyle \Omega (k)}$	рад / с	${\displaystyle {\sqrt {gk}}={\sqrt {\frac {2\pi \,g}{\lambda }}}}$	${\displaystyle k{\sqrt {gh}}={\frac {2\pi }{\lambda }}{\sqrt {gh}}}$	${\displaystyle {\begin{aligned}&{\sqrt {gk\,\tanh \left(kh\right)}}\,\\[1.2ex]&={\sqrt {{\frac {2\pi g}{\lambda }}\tanh \left({\frac {2\pi h}{\lambda }}\right)}}\,\end{aligned}}}$
фазовая скорость	${\displaystyle \displaystyle c_{p}={\frac {\lambda }{T}}={\frac {\omega }{k}}}$	РС	${\displaystyle {\sqrt {\frac {g}{k}}}={\frac {g}{\omega }}={\frac {g}{2\pi }}T}$	${\displaystyle {\sqrt {gh}}}$	${\displaystyle {\sqrt {{\frac {g}{k}}\tanh \left(kh\right)}}}$
групповая скорость	${\displaystyle \displaystyle c_{g}={\frac {\partial \Omega }{\partial k}}}$	РС	${\displaystyle {\frac {1}{2}}{\sqrt {\frac {g}{k}}}={\frac {1}{2}}{\frac {g}{\omega }}={\frac {g}{4\pi }}T}$	${\displaystyle {\sqrt {gh}}}$	${\displaystyle {\frac {1}{2}}c_{p}\left(1+{\frac {2kh}{\sinh \left(2kh\right)}}\right)}$
соотношение	${\displaystyle \displaystyle {\frac {c_{g}}{c_{p}}}}$	-	${\displaystyle \displaystyle {\frac {1}{2}}}$	${\displaystyle \displaystyle 1}$	${\displaystyle {\frac {1}{2}}\left(1+{\frac {2kh}{\sinh \left(2kh\right)}}\right)}$
длина волны	${\displaystyle \displaystyle \lambda }$	м	${\displaystyle {\frac {g}{2\pi }}T^{2}}$	${\displaystyle T{\sqrt {gh}}}$	для заданного периода T решение:   ${\displaystyle \displaystyle \left({\frac {2\pi }{T}}\right)^{2}={\frac {2\pi g}{\lambda }}\tanh \left({\frac {2\pi h}{\lambda }}\right)}$

Глубокая вода соответствует глубине воды, превышающей половину длины волны , что является обычной ситуацией в океане. На большой глубине волны с более длинным периодом распространяются быстрее и быстрее переносят свою энергию. Глубоководная групповая скорость составляет половину фазовой скорости . На мелководье для длин волн, превышающих глубину более чем в двадцать раз ^[14], что довольно часто встречается у берегов, групповая скорость равна фазовой скорости.

История [ править ]

Полное линейное соотношение дисперсии было впервые найдено Пьером-Симоном Лапласом , хотя в его решении линейной волновой задачи были некоторые ошибки. Полная теория линейных волн на воде, включая дисперсию, была получена Джорджем Бидделлом Эйри и опубликована примерно в 1840 году. Примерно в то же время подобное уравнение было также найдено Филипом Келландом (но с некоторыми ошибками при выводе теории волн) . ^[15]

Предел мелкой воды (с малым h / λ ), ω ² = gh k ² , был получен Джозефом Луи Лагранжем .

Эффекты поверхностного натяжения [ править ]

Рассеивание гравитационно-капиллярных волн на поверхности глубокой воды. Фаза и групповая скорость, деленные на как функция обратной относительной длины волны . Синие линии (A): фазовая скорость, красные линии (B): групповая скорость. Проведенные линии: дисперсионное соотношение для гравитационно-капиллярных волн. Пунктирные линии: дисперсионное соотношение для глубоководных гравитационных волн. Пунктирные линии: закон дисперсии для глубоководных капиллярных волн.${\displaystyle \scriptstyle {\sqrt[{4}]{g\sigma /\rho }}}$${\displaystyle \scriptstyle {\frac {1}{\lambda }}{\sqrt {\sigma /(\rho g)}}}$

В случае гравитационно-капиллярных волн, когда на волны влияет поверхностное натяжение , дисперсионное соотношение принимает вид ^[5]

${\displaystyle \omega ^{2}=\left(gk+{\frac {\sigma }{\rho }}k^{3}\right)\tanh(kh),}$

с σ поверхностным натяжением (в Н / м).

Для границы раздела вода-воздух (с σ = 0,074 Н / м и ρ = 1000 кг / м³ ) волны могут быть аппроксимированы чистыми капиллярными волнами, в которых преобладают эффекты поверхностного натяжения, для длин волн менее 0,4 см (0,2 дюйма). Для длин волн более 7 см (3 дюйма) волны в хорошем приближении являются чистыми поверхностными гравитационными волнами с очень небольшими эффектами поверхностного натяжения. ^[16]

Межфазные волны [ править ]

Для двух однородных слоев жидкости со средней толщиной h ниже границы раздела и h ′ сверху - под действием силы тяжести и ограниченных сверху и снизу горизонтальными жесткими стенками - для гравитационных волн обеспечивается дисперсионное соотношение ω ²  = Ω ² ( k ) автор: ^[17]

${\displaystyle \Omega ^{2}(k)={\frac {g\,k(\rho -\rho ')}{\rho \,\coth(kh)+\rho '\,\coth(kh')}},}$

где снова ρ и ρ ′ - плотности ниже и выше границы раздела, а coth - гиперболическая функция котангенса . Для случая, когда ρ ′ равно нулю, это сводится к закону дисперсии поверхностных гравитационных волн на воде конечной глубины h .

Когда глубина двух слоев жидкости становится очень большой ( h → ∞, h ′ → ∞), гиперболические котангенсы в приведенной выше формуле приближаются к значению единицы. Потом:

${\displaystyle \Omega ^{2}(k)={\frac {\rho -\rho '}{\rho +\rho '}}\,g\,k.}$

Нелинейные эффекты [ править ]

Мелководье [ править ]

Эффекты амплитудной дисперсии проявляются, например, в уединенной волне : одиночный выступ воды, движущийся с постоянной скоростью на мелководье с горизонтальным дном. Обратите внимание, что уединенные волны являются почти солитонами , но не совсем - после взаимодействия двух (сталкивающихся или догоняющих) уединенных волн они немного изменились по амплитуде и осталась осциллирующая невязка. ^[18] Односолитонное решение уравнения Кортевега – де Фриза для высоты волны H на глубине воды h вдали от гребня волны распространяется со скоростью:

${\displaystyle c_{p}=c_{g}={\sqrt {g(h+H)}}.}$

Таким образом, для этой нелинейной гравитационной волны именно общая глубина воды под гребнем волны определяет скорость, при этом более высокие волны распространяются быстрее, чем более низкие волны. Обратите внимание, что уединенные волновые решения существуют только для положительных значений H , уединенные гравитационные волны депрессии не существуют.

Глубокая вода [ править ]

Линейное дисперсионное соотношение - не зависящее от амплитуды волны - для нелинейных волн также верно во втором порядке разложения теории возмущений с порядками в терминах крутизны волны ka (где a - амплитуда волны ). Для третьего порядка и для глубокой воды дисперсионное соотношение имеет вид ^[19]

${\displaystyle \omega ^{2}=gk\left[1+(ka)^{2}\right],}$   так   ${\displaystyle c_{p}={\sqrt {\frac {g}{k}}}\,\left[1+{\tfrac {1}{2}}\,(ka)^{2}\right]+{\mathcal {O}}\left((ka)^{4}\right).}$

Это означает, что большие волны распространяются быстрее, чем маленькие с той же частотой. Это заметно только при большой крутизне волны ka .

Волны на среднем течении: Доплеровский сдвиг [ править ]

Волны на воде в среднем потоке (то есть волна в движущейся среде) испытывают доплеровский сдвиг . Предположим, что дисперсионное соотношение для неподвижной среды имеет вид:

${\displaystyle \omega ^{2}=\Omega ^{2}(k),\,}$

с k волновым числом. Тогда для среды с вектором средней скорости V дисперсионное соотношение с доплеровским сдвигом принимает вид ^[20]

${\displaystyle \left(\omega -\mathbf {k} \cdot \mathbf {V} \right)^{2}=\Omega ^{2}(k),}$

где k - вектор волнового числа, связанный с k следующим образом: k = | k |. Скалярное произведение к • V равна: к • V = кВ совы α , с V длиной среднего вектора скорости V : V = | V |, И & alpha ; угол между направлением распространения волны и направлением среднего потока. Для волн и тока в одном направлении k • V = кВ .

См. Также [ править ]

Другие статьи о дисперсии [ править ]

• Дисперсионное уравнение в частных производных
• Капиллярная волна

Модели дисперсионных волн на воде [ править ]

• Теория волн Эйри
• Уравнение Бенджамина – Бона – Махони
• Приближение Буссинеска (волны на воде)
• Кноидальная волна
• Уравнение Камассы – Холма
• Уравнение Дэви – Стюартсона
• Уравнение Кадомцева – Петвиашвили (также известное как уравнение КП)
• Уравнение Кортевега – де Фриза (также известное как уравнение КдФ)
• Вариационный принцип Люка
• Нелинейное уравнение Шредингера
• Уравнения мелкой воды
• Волновая теория Стокса
• Трохоидальная волна
• Волновая турбулентность
• Уравнение Уизема

Примечания [ править ]

Ссылки [ править ]

Внешние ссылки [ править ]

• Математические аспекты дисперсионных волн обсуждаются на Dispersive Wiki .