Конверт (волны)

Функции верхней и нижней огибающей для модулированной синусоидальной волны.

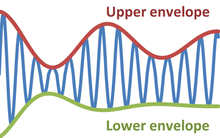
В физике и технике , то оболочка из осциллирующего сигнала является гладкой кривой с изложением своих экстремумов. ^[1] Таким образом, огибающая обобщает концепцию постоянной амплитуды до мгновенной амплитуды . На рисунке показана модулированная синусоида, изменяющаяся между верхней и нижней огибающей. Огибающая функция может быть функцией времени, пространства, угла или любой переменной.

Пример: бьющиеся волны [ править ]

Модулированная волна, полученная в результате сложения двух синусоидальных волн почти одинаковой длины и частоты.

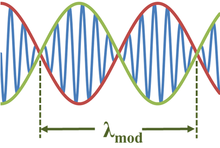
Обычная ситуация, приводящая к огибающей функции как в пространстве x, так и во времени t, является суперпозицией двух волн почти одинаковой длины волны и частоты: ^[2]

${\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}$

который использует тригонометрическую формулу для сложения двух синусоидальных волн и приближение Δ λ  ≪  λ :

${\displaystyle {\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.}$

Здесь длина волны модуляции λ _mod определяется как: ^{[2] [3]}

${\displaystyle \lambda _{\rm {mod}}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .}$

Длина волны модуляции вдвое больше длины самой огибающей, потому что каждая полуволна модулирующей косинусоидальной волны определяет как положительные, так и отрицательные значения модулированной синусоидальной волны. Аналогично, частота биений - это частота огибающей, в два раза превышающая частоту модулирующей волны, или 2Δ f . ^[4]

Если эта волна является звуковой волной, ухо слышит частоту, связанную с f, и амплитуда этого звука зависит от частоты биений. ^[4]

Фаза и групповая скорость [ править ]

Красный квадрат движется с фазовой скоростью , а зеленые кружки - с групповой скоростью .

Аргумент синусоид выше, за исключением множителя 2 π :

${\displaystyle \xi _{C}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,}$

${\displaystyle \xi _{E}=\left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\ ,}$

с индексами C и E, относящимися к перевозчику и конверту . Одна и та же амплитуда F волны является результатом одних и тех же значений ξ _C и ξ _E , каждое из которых само может возвращаться к одному и тому же значению при различных, но должным образом связанных выборах x и t . Эта инвариантность означает, что можно проследить эти формы волны в пространстве, чтобы найти скорость положения фиксированной амплитуды, когда оно распространяется во времени; для того, чтобы аргумент несущей волны оставался неизменным, выполняется условие:

${\displaystyle \left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,}$

который показывает, что для сохранения постоянной амплитуды расстояние Δ x связано с интервалом времени Δ t так называемой фазовой скоростью v _p

${\displaystyle v_{\rm {p}}={\frac {\Delta x}{\Delta t}}=\lambda f\ .}$

С другой стороны, те же соображения показывают, что оболочка распространяется с так называемой групповой скоростью v _g : ^[5]

${\displaystyle v_{\rm {g}}={\frac {\Delta x}{\Delta t}}=\lambda _{\rm {mod}}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .}$

Более общее выражение для групповой скорости получается путем введения волнового вектора k :

${\displaystyle k={\frac {2\pi }{\lambda }}\ .}$

Заметим, что для небольших изменений Δ λ величина соответствующего небольшого изменения волнового вектора, скажем Δ k , составляет:

${\displaystyle \Delta k=\left|{\frac {dk}{d\lambda }}\right|\Delta \lambda =2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,}$

поэтому групповая скорость может быть переписана как:

${\displaystyle v_{\rm {g}}={\frac {2\pi \Delta f}{\Delta k}}={\frac {\Delta \omega }{\Delta k}}\ ,}$

где ω - частота в радианах / с: ω = 2 π f . Во всех средствах массовой информации, частота и волновой вектор связаны с дисперсионным соотношением , ω = & omega ( K ), а групповая скорость может быть записано:

${\displaystyle v_{\rm {g}}={\frac {d\omega (k)}{dk}}\ .}$

Соотношение дисперсии ω = ω ( k ) для некоторых волн, соответствующих колебаниям решетки в GaAs. ^[6]

В такой среде, как классический вакуум, дисперсионное соотношение для электромагнитных волн имеет вид:

${\displaystyle \omega =c_{0}k}$

где c ₀ - скорость света в классическом вакууме. В этом случае фазовая и групповая скорости равны c ₀ .

В так называемых диспергирующих средах дисперсия может быть сложной функцией волнового вектора, и фазовые и групповые скорости не одинаковы. Например, для нескольких типов волн, проявляемых колебаниями атомов ( фононами ) в GaAs, на рисунке показаны дисперсионные соотношения для различных направлений волнового вектора k . В общем случае фазовая и групповая скорости могут иметь разные направления. ^[7]

Пример: аппроксимация огибающей функции [ править ]

В физике конденсированного состояния собственная функция энергии мобильного носителя заряда в кристалле может быть выражена как блоховская волна :

${\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )\ ,}$

где n - индекс зоны (например, зоны проводимости или валентной зоны), r - пространственное положение, а k - волновой вектор . Экспонента представляет собой синусоидально изменяющуюся функцию, соответствующую медленно изменяющейся огибающей, модулирующей быстро меняющуюся часть волновой функции u _{n , k,} описывающей поведение волновой функции вблизи ядер атомов решетки. Огибающая ограничена k-значениями в диапазоне, ограниченном зоной Бриллюэна кристалла, и это ограничивает скорость ее изменения в зависимости от местоположения r .

При определении поведения носителей с использованием квантовой механики , то приближение огибающего , как правило , используются , в котором уравнение Шредингера упрощается относится только к поведению оболочки, и граничные условия применяются к функции огибающей непосредственно, а не полному волновая функция. ^[9] Например, волновая функция носителя, захваченного вблизи примеси, определяется огибающей функцией F, которая управляет суперпозицией функций Блоха:

${\displaystyle \psi (\mathbf {r} )=\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }u_{\mathbf {k} }(\mathbf {r} )\ ,}$

где компоненты Фурье огибающей F ( k ) находятся из приближенного уравнения Шредингера. ^[10] В некоторых приложениях периодическая часть u _k заменяется ее значением около края зоны, скажем, k = k ₀ , а затем: ^[9]

${\displaystyle \psi (\mathbf {r} )\approx \left(\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }\right)u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )=F(\mathbf {r} )u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )\ .}$

Пример: дифракционные картины [ править ]

Дифракционные картины от нескольких щелей имеют огибающие, определяемые дифракционной картиной с одной щелью. Для одной щели образец задается следующим образом: ^[11]

${\displaystyle I_{1}=I_{0}\sin ^{2}\left({\frac {\pi d\sin \alpha }{\lambda }}\right)/\left({\frac {\pi d\sin \alpha }{\lambda }}\right)^{2}\ ,}$

где α - угол дифракции, d - ширина щели, λ - длина волны. Для нескольких прорезей используется шаблон ^[11]

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

где q - количество щелей, g - постоянная решетки. Первый фактор, результат I _{1 для} одной щели , модулирует более быстро меняющийся второй фактор, который зависит от количества щелей и их расстояния.

См. Также [ править ]

• Сложный конверт
• Разложение по эмпирическим модам
• Конверт (математика)
• Детектор конверта
• Отслеживание конвертов
• Мгновенная фаза
• Модуляция
• Математика колебаний
• Пиковая мощность огибающей
• Спектральная огибающая

Ссылки [ править ]

Эта статья включает материал из статьи Citizendium « Функция конверта », которая находится под лицензией Creative Commons Attribution-ShareAlike 3.0 Unported License, но не GFDL .