История математических обозначений [1] включает в себя начало, прогресс и культурное распространение в математических символах и конфликт методов нотации , сталкивающихся в движении нотации к популярности или незаметности. Математическая нотация [2] состоит из символов, используемых для написания математических уравнений и формул . Обозначения обычно подразумевают набор четко определенных представлений величин и операторов символов. [3] История включает индуистско-арабские цифры , буквы римского , греческого языков., Еврейский и немецкий алфавиты , а также множество символов, изобретенных математиками за последние несколько столетий.
Развитие математической записи можно разделить на этапы. [4] [5] На « риторическом » этапе вычисления выполняются словами, а символы не используются. [6] На этапе « синкопирования » часто используемые операции и количества представлены символьными синтаксическими сокращениями. С древних времен до постклассической эпохи [примечание 1] всплески математического творчества часто сменялись столетиями застоя. Когда наступила эпоха Нового времени и началось всемирное распространение знаний, появились письменные примеры математических разработок. " Символический«стадия, когда всеобъемлющие системы обозначений заменяют риторику. Начиная с Италии в 16 веке, новые математические разработки, взаимодействующие с новыми научными открытиями, делались все более быстрыми темпами, которые продолжаются и по сей день. Эта символическая система использовалась средневековыми Индийские математики и в Европе с середины 17 века [7] продолжали развиваться и в современную эпоху .
Область исследования, известная как история математики, - это прежде всего исследование происхождения открытий в математике и, в центре внимания, исследование математических методов и обозначений прошлого.
Риторический этап [ править ]
Хотя история начинается с истории ионийских школ , нет никаких сомнений в том, что те древние греки, которые обратили на нее внимание, во многом были обязаны предыдущим исследованиям древних египтян и древних финикийцев . Отличительная черта числового обозначения, т.е. символы, имеющие как локальные, так и внутренние значения ( арифметику ), подразумевает состояние цивилизации.в период его изобретения. Наши знания о математических достижениях этих древних народов, которым посвящен этот раздел, несовершенны, и следующие краткие заметки следует рассматривать как резюме выводов, которые кажутся наиболее вероятными, а история математики начинается с символических разделов.
Многие области математики начинались с изучения проблем реального мира до того, как основные правила и концепции были идентифицированы и определены как абстрактные структуры . Например, геометрия берет свое начало в вычислении расстояний и площадей в реальном мире; алгебра началась с методов решения задач по арифметике .
Нет сомнений в том, что большинство древних народов, сохранивших записи, кое-что знали о нумерации и механике , а некоторые были также знакомы с элементами топографической съемки . В частности, египтяне уделяли внимание геометрии и числам, а финикийцы - практической арифметике, бухгалтерскому учету , навигации и землеустройству. В результаты , полученные этими людьми , по- видимому, были доступны , при определенных условиях, для путешественников. Вероятно, что знания египтян и финикийцев были в значительной степени результатом наблюдений и измерений и представляли собой накопленный опыт многих веков.
Начало обозначений [ править ]
Письменная математика начиналась с чисел, выраженных в счетных отметках , где каждый счет представлял одну единицу. Числовые символы, вероятно, состояли из штрихов или выемок, вырезанных в дереве или камне, и были понятны всем народам. [примечание 2] Например, одна выемка в кости представляла одно животное, или человека, или что-то еще. Народы, с которыми греки Малой Азии (среди которых начинаются записи в западной истории), вероятно, часто вступали в контакт, были народами, населявшими восточное побережье Средиземного моря, и греческая традиция однозначно приписывала особое развитие геометрии египтянам. а наука о числах [примечание 3] - либо египтянам, либо финикийцам.
У древних египтян было символическое обозначение, которое исчислялось иероглифами . [8] [9] В египетской математике были символы: один, десять, сто, одна тысяча, десять тысяч, сто тысяч и один миллион. Меньшие цифры были помещены слева от числа, как в индусско-арабских цифрах. Позже египтяне использовали иератическое письмо вместо иероглифического письма для обозначения чисел. Иератик был больше похож на курсив и заменял несколько групп символов отдельными. Например, четыре вертикальные линии, используемые для представления четырех, были заменены одной горизонтальной линией. Это можно найти в Математическом папирусе Райнда.(ок. 2000–1800 до н. э.) и Московский математический папирус (ок. 1890 до н. э.). Система, которую использовали египтяне, была открыта и изменена многими другими цивилизациями Средиземноморья. У египтян также были символы для основных операций: ноги, идущие вперед, представляли сложение, а ноги, идущие назад, - вычитание.
У месопотамцев были символы для каждой степени десяти. [10] Позже они написали свои числа почти так же, как в наше время. Вместо того, чтобы иметь символы для каждой степени десяти, они просто поместили бы коэффициент этого числа. Каждая цифра была разделена пробелом, но ко времени Александра Великого они создали символ, который представлял ноль и был заполнителем. Жители Месопотамии также использовали шестидесятеричную систему счисления, то есть основание шестьдесят. Именно эта система используется в наше время для измерения времени и углов. Вавилонская математика основана на более чем 400 глиняных табличках, обнаруженных с 1850-х годов. [11] Написано клинописью.Таблички писали, пока глина была влажной и сильно запекалась в духовке или под воздействием солнечного тепла. Некоторые из них выглядят как домашние задания с оценками. Самые ранние свидетельства письменной математики относятся к древним шумерам, а система метрологии - к 3000 г. до н.э. Примерно с 2500 г. до н.э. шумеры писали таблицы умножения на глиняных табличках и решали геометрические упражнения и задачи деления . К этому периоду относятся и самые ранние следы вавилонских цифр. [12]
Большинство месопотамских глиняных табличек датируются 1800–1600 гг. До н.э. и охватывают темы, которые включают дроби, алгебру, квадратные и кубические уравнения, а также вычисление регулярных , взаимных и пар . [13] Таблички также включают таблицы умножения и методы решения линейных и квадратных уравнений . Вавилонская табличка YBC 7289 дает приближение √ 2 с точностью до пяти знаков после запятой. Вавилонская математика была написана с использованием шестидесятеричной системы счисления (с основанием 60).. Отсюда и происходит современное использование 60 секунд в минуту, 60 минут в час и 360 (60 × 6) градусов по кругу, а также использование минут и секунд дуги для обозначения долей градуса. . Вавилонскому прогрессу в математике способствовал тот факт, что 60 имеет много делителей: величина, обратная любому целому числу, кратному делителю 60, имеет конечное разложение по основанию 60 (в десятичной арифметике только обратные числа, кратные 2 и 5, имеют в конечных десятичных разложениях.) Кроме того, в отличие от египтян, греков и римлян, у вавилонян была настоящая система счисления знаков, в которой цифры, записанные в левом столбце, представляли большие значения, почти как в десятичном.система. Однако им не хватало эквивалента десятичной точки, и поэтому значение места символа часто приходилось выводить из контекста.
Синкопированный этап [ править ]
- Фетти (1620)
Последние слова, приписываемые Архимеду, - « Не тревожь мои круги » [примечание 4], ссылка на круги на математическом рисунке, который он изучал, когда его потревожил римский солдат.
Историю математики нельзя с уверенностью проследить до какой-либо школы или периода, предшествовавшего истории ионийских греков, но последующая история может быть разделена на периоды, различия между которыми достаточно хорошо заметны. Греческая математика, возникшая с изучения геометрии, с самого начала имела тенденцию к дедукции и научности. Начиная с четвертого века нашей эры, Пифагору обычно приписывают открытие теоремы Пифагора , теоремы в геометрии, которая утверждает, что в прямоугольном треугольнике площадь квадрата на гипотенузе (сторона, противоположная прямому углу) равна сумма площадей квадратов двух других сторон. [примечание 5]Древние математические тексты доступны с ранее упомянутой нотацией древних египтян и с Плимптоном 322 (вавилонская математика около 1900 г. до н.э.). Изучение математики как предмет в своем собственном праве начинается в 6 веке до н.э. с пифагорейцами , который ввел термин «математику» от древнегреческого μάθημα ( mathema ), что означает «предмет обучения». [14]
Влияние Платона было особенно сильным в математике и естественных науках. Он помог провести различие между чистой и прикладной математикой , увеличив разрыв между «арифметикой», которая теперь называется теорией чисел, и «логистикой», которая теперь называется арифметикой . Греческая математика значительно усовершенствовала методы (особенно за счет введения дедуктивного мышления и математической строгости в доказательствах ) и расширила предмет математики. [15] Аристотелю приписывают то, что позже будет названо законом исключенного третьего .
Абстрактная математика [16] - это то, что относится к величине [примечание 6] или количеству , абсолютно и обычно присваиваемой, без учета каких-либо видов конкретной величины, таких как арифметика и геометрия. В этом смысле абстрактная математика противопоставляется смешанной математике , в которой простые и абстрактные свойства и отношения величин, примитивно рассматриваемые в математике, применяются к чувствительным объектам и тем самым смешиваются с физическими соображениями, такими как гидростатика , оптика и навигация . [16]
Архимеда обычно считают величайшим математиком древности и одним из величайших математиков всех времен. [17] [18] Он использовал метод исчерпания для вычисления площади под дугой параболы с суммированием бесконечного ряда и дал удивительно точное приближение числа пи . [19] Он также определил спираль , носящую его имя, формулы для объемов от поверхностей вращения и изобретательной системы для выражения очень больших чисел.
Опора. 31, 32 и 33 книги Евклида XI, которая находится в т. 2 рукописи, листы с 207 по 208 лицевой.
В историческом развитии геометрии шаги к абстракции геометрии были сделаны древними греками. Элементы Евклида являются ранней существующей документацией аксиом плоскости Геометрия- хотя Прокл говорит о более раннем аксиоматизации по Гиппократ Хиоса . [20] Евклид элементы (. С 300 г. до н.э.) является одним из старейших сохранившихся греческих математических трактатов [примечание 7] и состоял из 13 книг , написанных в Александрии; сбор теорем, доказанных другими математиками, дополненный некоторыми оригинальными работами. [примечание 8]Документ представляет собой успешный сборник определений, постулатов (аксиом), утверждений (теорем и построений) и математических доказательств утверждений. Первая теорема Евклида - это лемма, которая обладает свойствами простых чисел . Тринадцать влиятельных книг охватывают евклидову геометрию, геометрическую алгебру и древнегреческую версию алгебраических систем и элементарной теории чисел. Это было повсеместно в Quadrivium и способствовало развитию логики, математики и науки.
Диофант Александрийский был автором серии книг под названием « Арифметика» , многие из которых сейчас утеряны. Эти тексты посвящены решению алгебраических уравнений . Боэций обеспечил место математике в учебной программе в VI веке, когда он ввел термин квадривиум для описания изучения арифметики, геометрии, астрономии и музыки. Он написал « De instante arithmetica» , вольный перевод с греческого « Введения в арифметику» Никомаха ; De Institée musica , также полученное из греческих источников; и серия отрывков из стихов Евклида.. Его работы были теоретическими, а не практическими, и были основой математических исследований до восстановления греческих и арабских математических работ. [21] [22]
Акрофоническая и милетская нумерация [ править ]
Греки использовали мансардное нумерацией , [23] , которая была основана на системе египтян , а позже была адаптирована и использована римлянами . Греческие цифры с первого по четвертый были вертикальными линиями, как в иероглифах. Символом пяти была греческая буква Π (пи), которая является буквой греческого слова, обозначающего пять, пенте . Номера с шестого по девятый были пенте с вертикальными линиями рядом с ними. Десять было представлено буквой (Δ) слова, обозначающим десять, дека , сто буквой слова, обозначающим сто, и т. Д.
Ионическое нумерация используется весь свой алфавит , включая три архаические буквы. Цифровое обозначение греков, хотя и гораздо менее удобное, чем то, что используется сейчас, было сформировано по совершенно регулярному и научному плану [24] и могло использоваться с приемлемым эффектом в качестве инструмента расчета, для чего использовалась римская система. совершенно неприменимо. Греки разделили двадцать четыре буквы своего алфавита на три класса и, добавив еще один символ к каждому классу, получили символы для обозначения единиц, десятков и сотен. ( Жана Батиста Жозефа Деламбра Astronomie Ancienne, т. II.)
| Α (α) | Β (β) | Г (γ) | Δ (δ) | Ε (ε) | Ϝ (ϝ) | Ζ (ζ) | Η (η) | θ (θ) | Ι (ι) | Κ (κ) | Λ (λ) | Μ (μ) | Ν (ν) | Ξ (ξ) | Ο (ο) | Π (π) | Ϟ (ϟ) | Ρ (ρ) | Σ (σ) | Τ (τ) | Υ (υ) | Φ (φ) | Χ (χ) | Ψ (ψ) | Ω (ω) | Ϡ (ϡ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Эта система появилась в третьем веке до нашей эры, до того, как буквы дигамма (Ϝ), коппа (Ϟ) и сампи (Ϡ) устарели. Когда буквы нижнего регистра стали отличаться от букв верхнего регистра, буквы нижнего регистра использовались как символы для обозначения. Умножение на тысячу было записано как девять чисел с чертой перед ними: таким образом, тысяча была ", α", две тысячи было ", β" и т. Д. M (для μὐριοι, как в "мириадах") было используется для умножения чисел на десять тысяч. Например, число 88 888 888 будет записано как M, ηωπη * ηωπη [25]
Греческие математические рассуждения были почти полностью геометрическими (хотя часто использовались для рассуждений о негеометрических предметах, таких как теория чисел ), и, следовательно, греков не интересовали алгебраические символы. Большое исключение было Диофант из Александрии , большой алгебраист. [26] Его Арифметика была одним из текстов, в которых использовались символы в уравнениях. Это не было полностью символическим, но гораздо более важным, чем предыдущие книги. Неизвестный номер был назван s. [27] Квадрат s был ; куб был ; четвертая степень была ; и пятая степень была . [28] [примечание 9]
Китайские математические обозначения [ править ]
Китайцы использовали цифры, очень похожие на систему подсчета голосов. [29] Номера с первого по четвертый были горизонтальными линиями. Пять - это крестик между двумя горизонтальными линиями; оно выглядело почти так же, как римская цифра десять. В настоящее время система huām используется только для отображения цен на китайских рынках или в традиционных рукописных счетах.
В истории китайцев были те, кто был знаком с науками арифметики, геометрии, механики, оптики, навигации и астрономии. Математика в Китае возникла независимо к XI веку до нашей эры. [30] Почти очевидно, что китайцы были знакомы с некоторыми геометрическими или, скорее, архитектурными орудиями; [примечание 10] с механическими машинами; [примечание 11]что они знали о характерных свойствах магнитной стрелки; и знали, что астрономические события происходят циклично. Китайцы того времени делали попытки классифицировать или расширить известные им правила арифметики или геометрии и объяснить причины явлений, с которыми они были знакомы заранее. Китайцы независимо разработали очень большие и отрицательные числа , десятичные дроби , десятичную систему с разрядами, двоичную систему , алгебру , геометрию и тригонометрию .
Китайская математика внесла ранний вклад, в том числе в систему счисления . [31] [32] Геометрическая теорема, известная древним китайцам, была известна и применима в определенных случаях (а именно, отношение сторон). [примечание 12] Им были также известны геометрические теоремы, которые можно продемонстрировать квазиэкспериментальным способом суперпозиции. В арифметике их познания, по-видимому, ограничивались искусством вычислений с помощью лебедя., а также возможность письменного выражения результатов. Наши знания о первых достижениях китайцев, какими бы незначительными они ни были, более полны, чем у большинства их современников. Таким образом, это поучительно и служит для иллюстрации того факта, что можно знать, что нация может обладать значительными навыками в прикладных искусствах, но наши знания более поздней математики, на которой основаны эти искусства, могут быть скудными. Знания китайской математики до 254 г. до н.э. несколько фрагментарны, и даже после этой даты рукописные традиции остаются неясными. Даты за столетия до классического периода обычно считаются предположительными китайскими учеными, если они не сопровождаются подтвержденными археологическими свидетельствами.
Как и в других ранних обществах, основное внимание уделялось астрономии с целью усовершенствования сельскохозяйственного календаря и другим практическим задачам, а не созданию формальных систем . Китайский совет по математике обязанности ограничивались ежегодной подготовки альманаха, даты и предсказания , в которых он регулируется. Древние китайские математики не разработали аксиоматический подход, но добились успехов в разработке алгоритмов и алгебре. Достижения китайской алгебры достигли своего апогея в 13 веке, когда Чжу Шицзе изобрел метод четырех неизвестных.
Предполагается, что в результате очевидных лингвистических и географических барьеров, а также содержания, китайская математика и математика древнего средиземноморского мира развивались более или менее независимо до того времени, когда Девять глав математического искусства достигли своего расцвета. окончательная форма, в то время как « Письма о счетах» и « Хуайнаньцзы» примерно современны классической греческой математике. Вероятен некоторый обмен идеями в Азии посредством известных культурных обменов, по крайней мере, с римских времен. Часто элементы математики ранних обществ соответствуют рудиментарным результатам, обнаруженным позже в таких областях современной математики, как геометрия или теория чисел . Теорема Пифагоранапример, было засвидетельствовано времен герцога Чжоу . Знание треугольника Паскаля также было показано, что существовали в Китае несколько веков до Паскаля , [33] , например, путем Шен Куо .
Состояние тригонометрии в Китае постепенно начало меняться и развиваться во время династии Сун (960–1279), когда китайские математики начали уделять больше внимания необходимости сферической тригонометрии в календарной науке и астрономических расчетах. [34] эрудит китайский ученый, математик и официальный Шен Куо (1031-1095) , используемые тригонометрические функции для решения математических задач хорд и дуг. [34] Сал Рестиво пишет, что работа Шэня о длинах дуг окружностей послужила основой для сферической тригонометрии, разработанной в 13 веке математиком и астрономом Го Шоуцзином (1231–1316). [35]Как утверждают историки Л. Гоше и Джозеф Нидхэм, Го Шоуцзин использовал сферическую тригонометрию в своих расчетах для улучшения календарной системы и китайской астрономии . [36] [37] Математическая наука в Китае будет включать в себя работу и обучение арабских миссионеров со знанием сферической тригонометрии, которые приехали в Китай в течение тринадцатого века.
Индийские и арабские цифры и обозначения [ править ]
Хотя происхождение нашей нынешней системы числовых обозначений является древним, нет сомнений в том, что она использовалась индусами более двух тысяч лет назад. Алгебраическая нотация индийского математика , Брахмагупты , был синкопированная . Сложение было обозначено размещением чисел рядом, вычитание - точкой над вычитаемым числом (число, которое нужно вычесть), деление - помещением делителя под делимым, аналогично нашим обозначениям, но без черты. Умножение, эволюция и неизвестные величины были представлены сокращениями соответствующих терминов. [38] индо-арабская цифра системаи правила использования его операций, используемые сегодня во всем мире, вероятно, эволюционировали в течение первого тысячелетия нашей эры в Индии и были переданы на Запад через исламскую математику. [39] [40]
Несмотря на название, арабские цифры имеют корни в Индии. Причиной этого некорректным является европейцы видели цифры , используемые в арабской книге, касается индуистского искусства расплаты , по Mohommed ибн Муса аль-Хорезми . Аль-Хваризми написал несколько важных книг по индусско-арабским цифрам и методам решения уравнений. Его книга по расчету с индуистским числительным , написанная около 825, наряду с работой Аль-Кинди , [примечание 13] сыграла важную роль в распространении индийской математики и индийские цифрна запад. Аль-Хорезми не называл цифры арабскими, но в нескольких латинских переводах тот факт, что цифры были индийскими по происхождению, был утерян. Слово алгоритм происходит от латинизации имени Аль-Хорезми, Algoritmi, и слово алгебра из названия одной из своих работ, Аль-Китаб аль-Мухтасар ¯Fi Хисаб аль-Gabr wa'l-мукабаля ( The Book на сжатый Расчет достройкой и балансировкой ).
Исламская математика развила и расширила математику, известную среднеазиатским цивилизациям. [41] Аль-Хваризми дал исчерпывающее объяснение алгебраического решения квадратных уравнений с положительными корнями, [42] и Аль-Хваризми должен был преподавать алгебру в элементарной форме и ради нее самого. [43] Аль-Хваризми также обсудил фундаментальный метод « редукции » и «уравновешивания», имея в виду перенос вычитаемых членов в другую сторону уравнения, то есть сокращение одинаковых членов на противоположных сторонах уравнения. Это операция, которую аль-Хваризми первоначально назвал аль-джабр . [44]Его алгебра также больше не была связана «с рядом проблем, которые нужно решить, а с изложением, которое начинается с примитивных терминов, в которых комбинации должны давать все возможные прототипы для уравнений, которые отныне явным образом составляют истинный объект исследования». Аль-Хваризми также изучал уравнение ради него самого и «в общем смысле, поскольку оно не просто возникает в процессе решения проблемы, но специально призвано определять бесконечный класс проблем». [45]
Аль-Караджи в своем трактате аль-Фахри расширяет методологию, чтобы включить целые степени и целые корни неизвестных величин. [примечание 14] [46] историк математики, Ф. Woepcke, [47] похвалил Аль-Караджа за то , что «первым , кто ввел теорию о алгебраическом исчислении .» В том же 10 веке Абул Вафа перевел произведения Диофанта на арабский язык. Ибн аль-Хайтам разработал аналитическую геометрию. Аль-Хайтам вывел формулу суммы четвертых степеней, используя метод, который легко обобщается для определения общей формулы суммы любых целых степеней. Аль-Хайтам выполнил интегрирование, чтобы найти объем параболоида , и смог обобщить свой результат для интегралов от многочленов до четвертой степени . [примечание 15] [48] В конце 11 - го века, Омар Хайям будет развиваться алгебраической геометрией , писал Обсуждение Трудности в Евклиде , [примечание 16] и написал на общем геометрическом решении кубических уравнений . Насир ад-Дин Туси(Насиреддин) добился успехов в сферической тригонометрии . Мусульманские математики в этот период включают добавление десятичной запятой к арабским цифрам .
Современные арабские цифровые символы, используемые во всем мире, впервые появились в исламской Северной Африке в 10 веке. Отличительный западноарабский вариант восточных арабских цифр начал появляться примерно в 10 веке в странах Магриба и Аль-Андалуса (иногда их называют цифрами губар , хотя этот термин не всегда принимается), которые являются прямым предком используемых современных арабских цифр. По всему миру. [49]
Многие греческие и арабские тексты по математике были затем переведены на латынь , что привело к дальнейшему развитию математики в средневековой Европе. В XII веке ученые путешествовали по Испании и Сицилии в поисках научных арабских текстов, в том числе Аль-Хваризми [примечание 17] и полного текста Элементов Евклида . [примечание 18] [50] [51] Одной из европейских книг, пропагандирующих использование цифр, была « Liber Abaci » Леонардо Пизанского, более известного как Фибоначчи . Liber Abaci более известна математической проблемой, которую Фибоначчи написал в ней о популяции кроликов. Рост населения оказалсяПоследовательность Фибоначчи , где член - это сумма двух предыдущих членов.
Символический этап [ править ]
- Символы по популярной дате введения
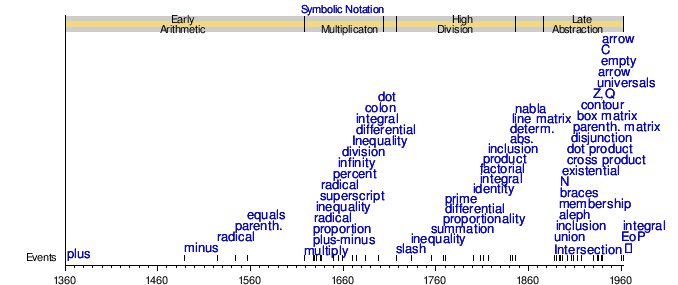
Ранняя арифметика и умножение [ править ]
Переход к символической алгебре, где используются только символы, впервые можно увидеть в работах Ибн аль-Банна аль-Марракуши (1256–1321) и Абу аль-Хасана ибн Али аль-Каладади (1412–1482). [52] [53] Аль-Каласади был последним крупным средневековым арабским алгебраистом , улучшившим алгебраические обозначения, ранее использовавшиеся в Магрибе Ибн аль-Банной. [54] В отличие от синкопированных обозначений своих предшественников, Диофанта и Брахмагупты , в которых отсутствовали символы для математических операций , [55]Алгебраическая нотация аль-Каласади была первой, в которой были символы для этих функций, и, таким образом, была «первым шагом к введению алгебраической символики». Он представлял математические символы, используя символы арабского алфавита . [54]
В 14 веке появились новые математические концепции для исследования широкого круга проблем. [56] Два широко используемых арифметических символа - это сложение и вычитание, + и -. Знак плюс использовался в 1360 году Николь Орем [57] [примечание 19] в его работе « Алгоризм пропорции» . [58] Считается, что это сокращение от «et», что означает «и» на латыни, во многом так же, как знак амперсанда также начинался как «et». Орем из Парижского университета и итальянец Джованни ди Казалинезависимо предоставили графические демонстрации расстояния, пройденного телом, совершающим равномерно ускоренное движение, утверждая, что площадь под линией, изображающей постоянное ускорение, представляет собой общее пройденное расстояние. [59] Знак минус использовался в 1489 году Иоганном Видманном в « Торговой арифметике» или « Behende und hüpsche Rechenung auff allen Kauffmanschafft» . [60] Видманн использовал символ «минус» со знаком «плюс» для обозначения дефицита и излишка, соответственно. [61] В Summa de arithmetica, geometria, пропорционально и пропорционально , [примечание 20] [62] Лука Пачолииспользовала символы плюса и минуса и содержала алгебру . [примечание 21]
В 15 веке Гият аль-Каши вычислил значение π до 16-го знака после запятой. У Каши также был алгоритм для вычисления корней n- й степени. [примечание 22] В 1533 году была опубликована таблица синусов и косинусов Региомонтана . [63] Сципионе дель Ферро и Никколо Фонтана Тарталья открыли решения для кубических уравнений . Джероламо Кардано опубликовал их в своей книге 1545 года Ars Magna вместе с решением уравнений четвертой степени , обнаруженным его учеником Лодовико Феррари . Радикал , символ[примечание 23] для квадратного корня было введено Кристофом Рудольфом . [примечание 24] Важная работа Майкла Стифеля Arithmetica integ [64] содержала важные нововведения в математической нотации. В 1556 году Никколо Тарталья использовал круглые скобки для группировки по старшинству. В 1557 году Роберт Рекорд опубликовал «Точильный камень» Витте, который ввел знак равенства (=), а также знаки плюс и минус для английского читателя. В 1564 году Джероламо Кардано проанализировал азартные игры, положив начало ранним этапам теории вероятностей . В 1572 году Рафаэль Бомбелли опубликовал свойL'Algebra, в которой он показал, как работать с мнимыми величинами, которые могут появиться в формуле Кардано для решения кубических уравнений. Книга Саймона Стевина De Thiende («Искусство десятых»), опубликованная на голландском языке в 1585 году, содержала систематическую трактовку десятичной системы счисления , которая повлияла на все последующие работы по действительной системе счисления . Новая алгебра (1591) из Виет ввел современные нотации манипуляции алгебраических выражений. Для навигации и создания точных карт больших территорий тригонометрия стала основным разделом математики. Bartholomaeus Pitiscusчеканить слово «тригонометрия», опубликовав свою « Тригонометрию» в 1595 году.
Джон Нэпьер наиболее известен как изобретатель логарифмов [примечание 25] [65] и сделал обычным использование десятичной точки в арифметике и математике. [66] [67] После Нэпьера, Эдмунд Гюнтер создал логарифмические шкалы (линии или правила), на которых основаны правила скольжения , именно Уильям Отред использовал две такие шкалы, скользящие друг относительно друга, для выполнения прямого умножения и деления ; и он считается изобретателем логарифмической линейки в 1622 году. В 1631 году Отред ввел знак умножения (×) в свой знак пропорциональности [примечание 26].и сокращения sin и cos для функций синуса и косинуса . [68] Альбер Жирар также использовал аббревиатуры «грех», «соз» и «загар» для тригонометрических функций в своем трактате.
Иоганн Кеплер был одним из пионеров математических приложений бесконечно малых . [примечание 27] Рене Декарт считается отцом аналитической геометрии , моста между алгеброй и геометрией [примечание 28], имеющего решающее значение для открытия исчисления бесконечно малых и анализа . В 17 веке Декарт ввел декартовы координаты, которые позволили развить аналитическую геометрию. [примечание 29] Блез Паскаль влиял на математику на протяжении всей своей жизни. Его черта арифметического треугольника(«Трактат об арифметическом треугольнике») 1653 г. описал удобное табличное представление биномиальных коэффициентов . [примечание 30] Пьер де Ферма и Блез Паскаль исследовали вероятность . [примечание 31] Джон Уоллис ввел символ бесконечности . [примечание 32] Он аналогичным образом использовал это обозначение для бесконечно малых. [примечание 33] В 1657 году Христиан Гюйгенс опубликовал трактат о вероятности « О рассуждении в играх с шансом» . [примечание 34] [69]
Иоганн Ран ввел знак деления (÷, измененный вариант обела) и знак, следовательно, в 1659 году. Уильям Джонс использовал π в Synopsis palmariorum mathesios [70] в 1706 году, потому что это начальная буква греческого слова периметрон (περιμετρον), которое означает периметр по-гречески. Это использование было популяризировано в 1737 году Эйлером. В 1734 году Пьер Бугер использовал двойную горизонтальную черту под знаком неравенства . [71]
Обозначение производных: Лейбниц и Ньютон [ править ]
| Производные обозначения | |
|---|---|
| |
Изучение линейной алгебры возникло из изучения определителей , которые использовались для решения систем линейных уравнений . В исчислении были две основные системы обозначений, каждая из которых была создана одним из создателей: система, разработанная Исааком Ньютоном, и система обозначений, разработанная Готфридом Лейбницем . Обозначения Лейбница используются сегодня чаще всего. Ньютон был просто точкой или тире, помещенной над функцией. [примечание 35] В современном использовании это обозначение обычно обозначает производные физических величин по времени и часто используется в науке механики . Лейбниц, с другой стороны, использовал букву dв качестве префикса для обозначения дифференциации и ввел обозначение, представляющее производные, как если бы они были особым типом дроби. [примечание 36] Это обозначение явно указывает переменную, по которой берется производная функции. Лейбниц также создал интегральный символ. [примечание 37] Символ представляет собой удлиненную букву S , представляющую латинское слово Summa , означающее «сумма». При нахождении областей под кривыми интеграция часто иллюстрируется разделением области на бесконечное множество высоких и тонких прямоугольников, области которых складываются. Таким образом, интегральный символ представляет собой удлиненную букву s для суммы.
Операторы и функции высокого уровня [ править ]
Буквы алфавита в это время должны были использоваться как символы количества ; и хотя существовало много разнообразия в выборе букв, в следующей истории должно было быть несколько общепризнанных правил . [24] Таким образом, здесь в истории уравнений первые буквы алфавита были обозначены как коэффициенты , а последние буквы - как неизвестные термины ( incerti ordinis ). В алгебраической геометрии , опять же, должно было соблюдаться аналогичное правило, где последние буквы алфавита обозначают переменные или текущие координаты . Некоторые буквы, такие как , ,и т. д. , были с всеобщего согласия присвоены как символы часто встречающихся чисел 3,14159 ... и 2,7182818 .... , [примечание 38] и т. д., и их использования в любом другом признании следовало избегать, насколько это возможно. [24] Буквы также должны были использоваться как символы операции, а вместе с ними и другие ранее упомянутые символы произвольной операции. Буквы , вытянутые должны были быть присвоены в качестве оперативных символов в дифференциальном исчислении и интегрального исчисления , и Е в исчислении различий . [24] В d {\ displaystyle d} S {\ displaystyle S} Δ {\ displaystyle \ Delta} В функциональных обозначениях одна буква, как символ операции, сочетается с другой, которая рассматривается как символ количества . [24] [примечание 39]
Начиная с 1718 года Томас Твинен использовал косую черту деления ( солидус ), получив ее от более ранней арабской горизонтальной черты дроби . Пьер-Симон, маркиз де Лаплас разработал широко используемый лапласовский дифференциальный оператор . [примечание 40] В 1750 году Габриэль Крамер разработал « правило Крамера » для решения линейных систем .
Эйлер и простые обозначения [ править ]
Леонард Эйлер был одним из самых плодовитых математиков в истории, а также плодотворным изобретателем канонической системы обозначений. Его вклад включает использование e для представления основания натуральных логарифмов . Точно неизвестно, почему было выбрано, но, вероятно, это произошло потому, что четыре буквы алфавита уже широко использовались для обозначения переменных и других констант. Эйлер последовательно представлял пи . Использование было предложено Уильямом Джонсом , который использовал его как сокращение для периметра . Эйлер представлял квадратный корень из отрицательного [примечание 41]хотя раньше он использовал это как бесконечное число. [примечание 42] [Примечание 43] Для суммирования Эйлера используется сигмы , Σ . [примечание 44] Для функций Эйлер использовал обозначение для представления функции от . В 1730 году Эйлер написал гамма-функцию . [примечание 45] В 1736 году Эйлер публикует свою статью о семи мостах Кенигсберга [72], положившую начало изучению теории графов .
Математик Уильям Эмерсон [73] разовьет знак пропорциональности . [примечание 46] [примечание 47] [74] [75] Намного позже в абстрактных выражениях значения различных пропорциональных явлений нотация частей на единицу станет полезной в качестве набора псевдоединиц для описания малых значений различных безразмерных величин. . Маркиз де Кондорсе в 1768 году предложил знак частичного дифференциала . [примечание 48] В 1771 году Александр-Теофиль Вандермонд вывел важность топологических особенностей при обсуждении свойств узлов.связанные с геометрией положения. Между 1772 и 1788 годами Жозеф-Луи Лагранж переформулировал формулы и расчеты классической «ньютоновской» механики, получившей название лагранжевой механики . Главный символ для производных также был сделан Лагранжем.
Но, на наш взгляд, истины такого рода следует извлекать из понятий, а не из нотаций.
- Карл Фридрих Гаусс [примечание 49]
Обозначения Гаусса, Гамильтона и Матрицы [ править ]
На рубеже 19-го века Карл Фридрих Гаусс разработал знак тождества для отношения конгруэнтности и, в квадратичной взаимности , интегральной части . Гаусс вклад функции от комплексных переменных , в геометрии , и о сходимости рядов . Он дал удовлетворительные доказательства основной теоремы алгебры и квадратичного закона взаимности . Гаусс разработал теорию решения линейных систем с использованием метода исключения Гаусса , который первоначально был отмечен как прогресс в геодезии .[76] Он также разработал знак продукта . Также в это время Нильс Хенрик Абель и Эварист Галуа [примечание 50] проводили свою работу по разрешимости уравнений , связывая теорию групп и теорию поля .
После 1800-х годов Кристиан Крамп будет продвигать факторную нотацию во время своих исследований обобщенной факторной функции, которая применяется к нецелым числам. [77] Джозеф Диас Жергонн ввел знаки включения множества . [примечание 51] Дирихле разработал Дирихль L -функции дать доказательство теоремы Дирихля об арифметических прогрессиях и начал аналитическую теорию чисел . [примечание 52] В 1828 году Гаусс доказал свою теорему Egregium ( замечательная теоремана латыни), устанавливая свойство поверхностей. В 1830-х годах Джордж Грин разработал функцию Грина . В 1829 г. Карл Густав Якоб Якоби публикует Fundamenta nova theoriae functionum ellipticarum со своими эллиптическими тета-функциями . К 1841 году Карл Вейерштрасс , «отец современного анализа », разработал концепцию абсолютного значения и определителя матрицы .
Матричные обозначения были бы более полно развиты Артуром Кэли в его трех статьях, по темам, которые были предложены при чтении Mécanique analytique [78] Лагранжа и некоторых работ Лапласа. Кэли определяется умножение матриц и матричных инверсий . Кэли использовал одну букву для обозначения матрицы [79], таким образом рассматривая матрицу как агрегированный объект. Он также осознал связь между матрицами и детерминантами [80] и написал: « Можно много чего сказать об этой теории матриц, которая, как мне кажется, должна предшествовать теории детерминантов ». [81]
[... Математический кватернион] имеет или, по крайней мере, включает ссылку на четыре измерения.
- Уильям Роуэн Гамильтон [примечание 53]
Уильям Роуэн Гамильтон ввел бы символ набла [примечание 54] для векторных дифференциалов . [82] [83] Ранее это использовалось Гамильтоном как знак оператора общего назначения . [84] Гамильтон переформулировал механику Ньютона , которая теперь называется гамильтоновой механикой . Эта работа оказалась центральной в современном исследовании классических теорий поля, таких как электромагнетизм . Это также было важно для развития квантовой механики . [примечание 55] В математике он, пожалуй, наиболее известен как изобретатель кватернионной нотации [примечание 56]и бикватернионы . Гамильтон также ввел слово « тензор » в 1846 году. [85] [примечание 57] Джеймс Кокл разработал тессарины [примечание 58], а в 1849 году - кокватернионы . В 1848 году Джеймс Джозеф Сильвестр ввел в матричную алгебру термин « матрица» . [примечание 59]
Обозначения Максвелла, Клиффорда и Риччи [ править ]
Самым выдающимся достижением Максвелла была формулировка системы уравнений , объединивших ранее не связанные наблюдения, эксперименты и уравнения электричества , магнетизма и оптики в единую теорию. [86]
В 1864 году Джеймс Клерк Максвелл свел все современные на тот момент знания об электромагнетизме в связанный набор дифференциальных уравнений с 20 уравнениями с 20 переменными, содержащийся в «Динамической теории электромагнитного поля» . [87] (См. Уравнения Максвелла .) Метод расчета, который необходимо использовать, был дан Лагранжем и впоследствии развит с некоторыми изменениями уравнениями Гамильтона . Обычно это называют принципом Гамильтона ; когда используются уравнения в исходной форме, они известны как уравнения Лагранжа . В 1871 году Ричард Дедекиндназывается набор действительных или комплексных чисел, который закрывается под четырьмя арифметическими операциями полем . В 1873 году Максвелл представил «Трактат об электричестве и магнетизме» .
В 1878 году Уильям Кингдон Клиффорд опубликовал свои « Элементы динамики» . [88] Clifford разработали сплит-Бикватернионы , [примечание 60] , которые он назвал алгебраические двигатели . Клиффорд отказался от исследования кватернионов, отделив скалярное произведение и векторное произведение двух векторов от полной записи кватернионов. [примечание 61] Этот подход сделал векторное исчисление доступным для инженеров и других специалистов, работающих в трех измерениях и скептически относящихся к эффекту опережения-отставания [примечание 62] в четвертом измерении .[Примечание 63] Общий вектор обозначение используется при работе с векторамикоторые являются пространственными или более абстрактными членами векторных пространств ,то время как угол обозначение (или Фазор обозначение) представляет собой обозначениеиспользуемое в электронике .
В 1881 году Леопольд Кронекера определили , что он назвал «домен рациональности», который является расширением поля в поле рациональных чисел в современных условиях. [89] В 1882 году Хусейн Тевфик Паша написал книгу под названием «Линейная алгебра». [90] [91] Лорд Кельвин «s эфирная теория атома (1860) привел Питер Guthrie Tait , в 1885 году, чтобы опубликовать топологическую таблицу узлов до десяти переездов , известных как догадки Tait . В 1893 году Генрих М. Вебер дал четкое определениеабстрактное поле . [Примечание 64] Тензорное исчисление был разработан Риччи-Курбастро между 1887-96, который был представлен в 1892 году под названием абсолютное дифференциальное исчисление , [92] и современного использования «тензора» высказал Woldemar Voigt в 1898. [93] В 1895 году Анри Пуанкаре опубликовал « Анализ Situs» . [94] В 1897 году Чарльз Протеус Стейнмец опубликует « Теорию и расчет явлений переменного тока» с помощью Эрнста Дж. Берга. [95]
От формульной математики к тензорам [ править ]
Вышеупомянутое предложение иногда бывает полезным.
- Бертран Рассел [примечание 65]
В 1895 Пеано выпустил свой Formulario математико , [96] усилие , чтобы переварить математику в лаконичный текст на основе специальных символов. Он дал бы определение векторного пространства и линейной карты . Он также ввел бы знак пересечения , в знак накидной , в знак членства (элемент), и экзистенциального квантора [примечание 66] (существует). Пеано передаст Бертрану Расселу свою работу в 1900 году на конференции в Париже; это так впечатлило Рассела, что Рассел тоже был увлечен стремлением передать математику более кратко. Результат былPrincipia Mathematica написана с Альфредом Норт Уайтхедом . Этот трактат знаменует собой переломный момент в современной литературе, где символ стал доминирующим. [примечание 67] Риччи-Курбастро и Туллио Леви-Чивита популяризировали обозначение тензорного индекса примерно в 1900 году. [97]
Математическая логика и абстракция [ править ]
| Абстракция | |
|---|---|
| |
В начале этого периода « Эрлангенская программа » Феликса Кляйна определила основную тему различных геометрий, определяя каждую из них как исследование свойств, инвариантных относительно данной группы симметрий . Этот уровень абстракции выявил связи между геометрией и абстрактной алгеброй . Георг Кантор [примечание 68] ввел бы символ алеф для кардинальных чисел трансфинитных множеств. [примечание 69] Его обозначение количественных чисел было еврейской буквой ( алеф ) с нижним индексом натурального числа; для ординалов он использовал греческую букву ω (омега ). Эта нотация все еще используется сегодня в порядковой нотации конечной последовательности символов из конечного алфавита, который называет порядковый номер в соответствии с некоторой схемой, придающей смысл языку. Его теория создала много споров . Кантор в своем исследовании рядов Фурье рассматривал точечные множества в евклидовом пространстве .
На рубеже 20-го века Джозия Уиллард Гиббс в физической химии ввел среднюю точку для скалярного произведения и знак умножения для перекрестных произведений . Он также предоставил обозначения для скалярных и векторных произведений, которые были введены в векторном анализе . В 1904 году Эрнст Цермело продвигает аксиому выбора и свое доказательство теоремы о хорошем порядке . [98] Вскоре после этого Бертран Рассел ввел логическую дизъюнкцию ( ИЛИ ) в 1906 году. Также в 1906 году Пуанкаре опубликовалО динамике электрона [99] и Морис Фреше ввели метрическое пространство . [100] Позже Герхард Ковалевски и Катберт Эдмунд Куллис [101] [102] [103] последовательно вводили обозначения матриц, матрицы в скобках и обозначения матриц ячеек соответственно. После 1907 г. математики [примечание 70] изучали узлы с точки зрения группы узлов и инварианты сточки зрения теории гомологий . [примечание 71] В 1908 годуструктурные теоремы Джозефа Веддерберна были сформулированы для конечномерных алгебр над полем.. Кроме того, в 1908 год Цермело предложил «определенное» свойство и первую теорию множеств аксиомы , Цермела теорию множеств . В 1910 году Эрнст Стейниц опубликовал влиятельную статью « Алгебраическая теория полей» . [примечание 72] [примечание 73] В 1911 году Стейнмец опубликует « Теорию и расчет переходных электрических явлений и колебаний» .
Альберт Эйнштейн в 1916 году ввел обозначения Эйнштейна [примечание 74], которые суммировали по набору проиндексированных членов в формуле, тем самым придавая краткость обозначениям. Арнольд Зоммерфельд создал знак контурного интеграла в 1917 году. Также в 1917 году Димитрий Мириманов предложил аксиому регулярности . В 1919 году Теодор Калуца решал уравнения общей теории относительности с использованием пяти измерений , в результате чего возникали электромагнитные уравнения. [104] Это будет опубликовано в 1921 году в «Zum Unitätsproblem der Physik». [105] В 1922 г.Авраам Френкель и Thoralf Skolem независимо предложили заменить схему выделения с аксиомой схемой замещения . В том же 1922 году была разработана теория множеств Цермело – Френкеля . В 1923 году Стейнмец опубликует « Четыре лекции по теории относительности и космосу» . Примерно в 1924 году Ян Арнольдус Схоутен разработал современные обозначения и формализм для структуры исчисления Риччи во время приложений абсолютного дифференциального исчисления к общей теории относительности и дифференциальной геометрии в начале двадцатого века. [примечание 75] [106] [107] [108]В 1925 году Энрико Ферми описал систему, состоящую из множества идентичных частиц, которые подчиняются принципу исключения Паули , а затем разработал уравнение диффузии ( уравнение Фермиджа ). В 1926 году Оскар Клейн разработал теорию Калуцы – Клейна . В 1928 году Эмиль Артин абстрагировал теорию колец с помощью артиновых колец . В 1933 году Андрей Колмогоров вводит аксиомы Колмогорова . В 1937 году Бруно де Финетти вывел понятие « операционально-субъективное » .
Математический символизм [ править ]
Математическая абстракция началась как процесс извлечения основной сущности математической концепции, [109] [110] устранения любой зависимости от объектов реального мира, с которыми она могла быть изначально связана, [111] и ее обобщения, чтобы она имела более широкие применения. или сопоставление среди других абстрактных описаний эквивалентных явлений . Два абстрактных областей современной математики теория категорий и теория моделей . Бертран Рассел [112] сказал: "Обычный язык совершенно не подходит для выражения того, что на самом деле утверждает физика, поскольку слова повседневной жизни недостаточно абстрактны. Только математика и математическая логика могут сказать так мало, как хочет сказать физик ». Хотя можно заменить математикой объекты реального мира, блуждать по уравнению за уравнением и построить концептуальную структуру, не имеющую отношения к реальности. [ 113]
Символическая логика изучает чисто формальные свойства цепочек символов. Интерес к этой области проистекает из двух источников. Во-первых, обозначения, используемые в символической логике, можно рассматривать как представление слов, используемых в философской логике . Во-вторых, правила манипулирования символами, найденные в символьной логике, могут быть реализованы на вычислительной машине . Символическая логика, как правило , делится на два подполя, пропозициональной логики и логики предикатов . Другие представляющие интерес логики включают темпоральную логику , модальную логику и нечеткую логику . Область символической логики, называемая логикой высказываний , также называемая исчислением высказываний., изучает свойства предложений, образованных из констант [примечание 76] и логических операторов . Соответствующие логические операции известны, соответственно, как конъюнкция , дизъюнкция , материальное условное , двусмысленное и отрицание . Эти операторы обозначаются ключевыми словами [примечание 77] и символическими обозначениями.
Некоторые из введенных в то время обозначений математической логики включали набор символов, используемых в булевой алгебре . Он был создан Джорджем Булем в 1854 году. Сам Буль не считал логику разделом математики, но она все равно была охвачена. Символы, встречающиеся в булевой алгебре, включают (И), (ИЛИ) и ( не ). С этими символами и буквами , чтобы представлять разные значения истинности , можно сделать логические операторы , такие как , то есть «( правда ИЛИ это не верно) истинно», это означает , что это правда , чтолибо верно, либо неверно (т.е. ложно). Булева алгебра сама по себе имеет множество практических применений, но она также положила начало тому, что могло бы стать большим набором символов, которые будут использоваться в логике. [примечание 78] Логика предикатов, первоначально называвшаяся исчислением предикатов , расширяет логику высказываний за счет введения переменных [примечание 79] и предложений, содержащих переменные, называемых предикатами . [примечание 80] Кроме того, логика предикатов позволяет использовать кванторы . [примечание 81] С помощью этих логических символов и дополнительных квантификаторов из логики предикатов [примечание 82] могут быть сделаны достоверные доказательства которые нерационально искусственные , [примечание 83] , но синтаксические. [примечание 84]
Обозначение неполноты Гёделя [ править ]
Для каждого со-последовательных рекурсивного класса К формулам соответствуют рекурсивным признакам класса г , таким , что ни v Gen г , ни отр ( v Gen г ) принадлежит Flg (х) (где v является свободным переменным из г ).
- Курт Гёдель [114]
При доказательстве его неполноте теоремы , [примечание 85] Курт Гедель создал альтернативу символов , обычно используемых в логике. Он использовал числа Гёделя , которые представляли собой операции с множеством чисел, и переменные с простыми числами больше 10. С помощью чисел Гёделя логические утверждения могут быть разбиты на числовую последовательность. Затем Гёдель пошел дальше, взяв n простых чисел и положив их в степень числа в последовательности. Затем эти числа были перемножены, чтобы получить конечный продукт, присвоив каждому логическому утверждению свой номер. [115] [примечание 86]
Современные обозначения и темы [ править ]
Обозначения начала 20-го века [ править ]
Абстракция обозначений - это непрерывный процесс, и историческое развитие многих математических тем демонстрирует прогрессию от конкретного к абстрактному. Для основных наборов объектов будут разработаны различные обозначения наборов . Примерно в 1924 году Дэвид Гильберт и Ричард Курант опубликовали « Методы математической физики. Уравнения с частными производными ». [116] В 1926 году Оскар Клейн и Уолтер Гордон предложили уравнение Клейна – Гордона для описания релятивистских частиц. [примечание 87] Первая формулировка квантовой теорииописание взаимодействия излучения и материи принадлежит Полю Адриену Морису Дираку , который в 1920 году впервые смог вычислить коэффициент спонтанного излучения атома . [117] В 1928 году Дирак сформулировал релятивистское уравнение Дирака, чтобы объяснить поведение релятивистски движущегося электрона . [примечание 88] Дирак описал количественную оценку электромагнитного поля как ансамбля гармонических осцилляторов с введением концепции операторов рождения и уничтожения частиц. В последующие годы при участии Вольфганга Паули ,Юджин Вигнер , Паскуаль Иордан , и Вернер Гейзенберг и элегантный формулировка квантовой электродинамики в связи с Энрико Ферми , [118] физики пришли к убеждению , что, в принципе, можно было бы выполнить любое вычисление для любого физического процесса с участием фотонов и заряженных частицы.
В 1931 году Александру Прока разработал уравнение Прока ( уравнение Эйлера – Лагранжа ) [примечание 89] для векторной мезонной теории ядерных сил и уравнений релятивистского квантового поля . Джон Арчибальд Уиллер в 1937 году разрабатывает S-матрицу . Исследования Феликса Блоха с Арнольдом Нордсиком , [119] и Виктор Вайскопф , [120] в 1937 и 1939 годах, показали , что такие расчеты были достоверными только в первом порядке теории возмущений , проблема уже указывалРоберт Оппенгеймер . [121] На более высоких порядках в рядах возникали бесконечности, делающие такие вычисления бессмысленными и вызывающие серьезные сомнения во внутренней непротиворечивости самой теории. Поскольку в то время не было известно решения этой проблемы, казалось, что существует фундаментальная несовместимость между специальной теорией относительности и квантовой механикой .
В 1930-е годы Эдмунд Ландау создал двойную заглавную букву Z для целых чисел . Николя Бурбаки создал двойную заглавную букву Q для наборов рациональных чисел. В 1935 году Герхард Гентцен создал универсальные кванторы . В 1936 году Альфред Тарский сформулировал и доказал теорему Тарского о неопределенности . [примечание 90] В 1938 году Гёдель предлагает конструируемую вселенную в статье « Согласованность аксиомы выбора и обобщенной гипотезы континуума ». Андре Вейль и Николя Бурбаки разработали пустой наборподписали в 1939 году. В том же году Натан Джейкобсон чеканил двойную заглавную букву C для комплексных числовых наборов.
Примерно в 1930-х годах для полилинейной алгебры была разработана нотация Фойгта [примечание 91] как способ представления симметричного тензора путем уменьшения его порядка. Обозначения Шенфлиса [примечание 92] стали одним из двух соглашений, используемых для описания точечных групп ( второе - обозначение Германа – Могена ). Также в это время стали популярными обозначения Ван-дер-Вардена [122] [123] для использования двухкомпонентных спиноров ( спиноров Вейля ) в четырех измерениях пространства-времени. Аренд Гейтинг представит алгебру Гейтинга иАрифметика Гейтинга .
Стрелка, например, →, была разработана для обозначения функций в 1936 году Ойстейном Оре для обозначения изображений определенных элементов. [примечание 93] [примечание 94] Позже, в 1940 году, он принял свою нынешнюю форму, например, f: X → Y , благодаря работам Витольда Гуревича . Вернер Гейзенберг в 1941 году предложил S-матричную теорию взаимодействий частиц.
Обозначение Брэ-Кет ( обозначение Дирака ) - это стандартное обозначение для описания квантовых состояний , состоящее из угловых скобок и вертикальных полос . Его также можно использовать для обозначения абстрактных векторов и линейных функционалов . Это так называемый , потому что внутренний продукт (или скалярное произведение на комплексном векторном пространстве) двух состояний обозначается ⟨bra | ket⟩ [примечание 95] , состоящий из левой части, ⟨ ф |, а правая часть, | г | ⟩. Обозначения была введена в 1939 году Поль Дирак , [124] , хотя обозначение имеет предшественников вИспользование Грассманом обозначения [ φ | ψ ] для своих внутренних продуктов почти 100 лет назад. [125]
Обозначения Брэкет широко распространены в квантовой механике : почти каждое явление, которое объясняется с помощью квантовой механики, включая большую часть современной физики , обычно объясняется с помощью нотации Брэкет. Обозначения устанавливают кодированную абстрактное представление-независимость, производя универсальный конкретное представление (например, х или р , или собственной функция базы) без особых проволочек или чрезмерных зависимости от, по природе из линейных пространств , участвующих. Выражение перекрытия ⟨ ф | г | ⟩ , как правило , интерпретируется как амплитуда вероятности длясостояние ψ , чтобы рухнуть в состояние ф . Фейнман слэш обозначение (Дирак слэш обозначения [126] ) был разработан Ричард Фейнман для изучения полей Дирака в квантовой теории поля .
В 1948 году Валентин Баргманн и Юджин Вигнер предложили релятивистские уравнения Баргмана – Вигнера для описания свободных частиц, которые имеют форму многокомпонентных волновых функций спинорного поля . В 1950 году Уильям Валланс Дуглас Ходж представил « Топологические инварианты алгебраических многообразий » на Трудах Международного конгресса математиков. Между 1954 и 1957 годами Эудженио Калаби работал над гипотезой Калаби для кэлеровых метрик и разработкой многообразий Калаби – Яу . В 1957 г.Туллио Редже сформулировал математическое свойство потенциального рассеяния в уравнении Шредингера . [примечание 96] Стэнли Мандельштам вместе с Редже разработали реджевскую теорию феноменологии сильного взаимодействия. В 1958 году Мюррей Гелл-Манн и Ричард Фейнман , наряду с Джорджем Сударшану и Роберта Маршака , вывел хиральных структур на слабое взаимодействие в физике. Джеффри Чу , наряду с другими, будет продвигать матричную запись для сильного взаимодействия и связанных с нимпринцип бутстрапа , в 1960 году. В 1960-х годах была разработана нотация конструктора множеств для описания множества посредством указания свойств, которым должны удовлетворять его члены. Также в 1960-х годах тензоры абстрагировались в рамках теории категорий с помощью концепции моноидальной категории . Позже многоиндексная нотация устраняет традиционные понятия, используемые в многомерном исчислении , уравнениях в частных производных и теории распределений , путем абстрагирования концепции целочисленного индекса до упорядоченного набора индексов.
Современные математические обозначения [ править ]
В современной математике специальной теории относительности , электромагнетизма и теории волн , то оператор Даламбера [примечание 97] [примечание 98] является оператор Лапласа в пространстве Минковского . Символ Леви-Чивита [примечание 99] используется в тензорном исчислении .
После полных формулировок ковариации Лоренца , конечных в любом порядке в ряду возмущений квантовой электродинамики, Син-Итиро Томонага , Джулиан Швингер и Ричард Фейнман были совместно награждены Нобелевской премией по физике в 1965 году. [127] Их вклад и вклад из Freeman Dyson , были о ковариантных и калибровочных инвариантных формулировках квантовой электродинамики , которые позволяют расчеты наблюдаемых в любом порядке теории возмущений . Математическая техника Фейнмана, основанная на его диаграммах , поначалу казалась очень отличной от теоретико-полевой,основанный на операторах подход Швингера и Томонаги, но позже Фриман Дайсон показал, что эти два подхода эквивалентны. Перенормировка , необходимость придать физический смысл некоторым расхождениям, появляющимся в теории, через интегралы , впоследствии стала одним из фундаментальных аспектов квантовой теории поля и стала рассматриваться как критерий общей приемлемости теории. Квантовая электродинамика послужила моделью и шаблоном для последующих квантовых теорий поля. Питер Хиггс , Джеффри Голдстоун и другие, Шелдон Глэшоу , Стивен Вайнберг и Абдус Саламнезависимо показали, как слабое ядерное взаимодействие и квантовая электродинамика могут быть объединены в одну электрослабую силу . В конце 1960-х годов зоопарк частиц состоял из известных тогда элементарных частиц до открытия кварков .
В фундаментальных фермионов и фундаментальных бозонов . (c.2008) [примечание 100] На основе собственной публикации , обзор физики элементарных частиц . [примечание 101]
Шагом к Стандартной модели стало открытие Шелдоном Глэшоу в 1960 году способа сочетать электромагнитное и слабое взаимодействия . [128] В 1967 году Стивен Вайнберг [129] и Абдус Салам [130] включили механизм Хиггса [131] [132] [133] в электрослабую теорию Глэшоу , придав ей современную форму. Считается, что механизм Хиггса определяет массы всех элементарных частиц Стандартной модели. Сюда входят массы W- и Z-бозонов, а также массы фермионов - кварков и лептонов . Также в 1967 году Брайс ДеВитт опубликовал свое уравнение под названием « уравнение Эйнштейна – Шредингера » (позже переименованное в « уравнение Уиллера – ДеВитта »). [134] В 1969 году Йоитиро Намбу , Хольгер Бек Нильсен и Леонард Сасскинд описали пространство и время в терминах струн . В 1970 году Пьер Рамон разработал двумерные суперсимметрии. Мичио Каку и Кейджи Киккававпоследствии сформулировал бы строковые вариации. В 1972 году Майкл Артин , Александр Гротендик , Жан-Луи Вердье предложили вселенную Гротендика . [135]
После нейтральных слабых токов, вызванных
Z
бозонный обмен был открыт в ЦЕРНе в 1973 г. [136] [137] [138] [139] теория электрослабого взаимодействия получила широкое признание, и Глэшоу, Салам и Вайнберг разделили Нобелевскую премию по физике 1979 г. за ее открытие. Теория сильного взаимодействия , в которую многие внесли свой вклад, приобрела свою современную форму примерно в 1973–74. С созданием квантовой хромодинамики был разработан окончательный набор фундаментальных и обменных частиц, что позволило создать « стандартную модель », основанную на математике калибровочной инвариантности., который успешно описывает все силы, кроме силы тяжести, и который остается общепринятым в той области, к которой он предназначен. В конце 1970-х годов Уильям Терстон ввел гиперболическую геометрию в изучение узлов с помощью теоремы гиперболизации . Система обозначений орбифолда , изобретенная Терстоном, была разработана для представления типов групп симметрии в двумерных пространствах постоянной кривизны. В 1978 году Шинг-Тунг Яу пришел к выводу, что гипотеза Калаби имеет плоскую метрику Риччи . В 1979 году Даниэль Фриданпоказал , что уравнения движения теории струн являются абстракциями уравнений Эйнштейна в общей теории относительности .
Первая революция суперструн состоит из математических уравнений , разработанных в период между 1984 и 1986. В 1984, Vaughan Jones вывел полином Джонса и последующие вклады от Виттен , Максим Концевич и другие, показали глубокие связи между теорией узлов и математических методов в статистической механике и квантовая теория поля. Согласно теории струн , все частицы в «зоопарке частиц» имеют общего предка - вибрирующую струну . В 1985 году Филип Канделас , Гэри Горовиц , [140] Эндрю Строминджер, а Эдвард Виттен опубликует «Вакуумные конфигурации для суперструн» [141]. Позднее тетрадный формализм ( обозначение тетрадного индекса ) будет введен как подход к общей теории относительности, который заменяет выбор координатного базиса менее ограничивающим выбором локального базис для касательного расслоения. [примечание 102] [142]
В 1990-х Роджер Пенроуз предложил графическую нотацию Пенроуза ( нотацию тензорной диаграммы ) как визуальное изображение полилинейных функций или тензоров , обычно рукописное . [143] Пенроуз также ввел бы абстрактные индексные обозначения . [примечание 103] В 1995 году Эдвард Виттен предложил М-теорию и впоследствии использовал ее для объяснения некоторых наблюдаемых двойственностей , положив начало второй революции суперструн . [примечание 104]
Джон Конвей будет далее различные обозначения, включая обозначения конвея , в Conway обозначения теории узлов , а многогранник обозначения Conway . Система обозначений Кокстера классифицирует группы симметрии, описывая углы между фундаментальными отражениями группы Кокстера . Он использует обозначения в квадратных скобках с модификаторами для обозначения определенных подгрупп. Обозначение названо в честь HSM Coxeter, и Норман Джонсон дал ему более полное определение.
Комбинаторная нотация LCF [примечание 105] была разработана для представления кубических графов, которые являются гамильтоновыми . [144] [145] обозначение цикла является соглашением для записи вниз перестановок в терминах его составных циклов . [146] Это также называется циклической нотацией, а перестановка - циклической или циклической перестановкой. [147]
Компьютеры и обозначения разметки [ править ]
В 1931 году IBM выпускает пробойник для умножения IBM 601 ; это электромеханическая машина, которая может считывать с карты два числа длиной до 8 цифр и наносить их продукт на ту же карту. [148] В 1934 году Уоллес Эккерт использовал оснастку IBM 601 Multiplying Punch для автоматизации интегрирования дифференциальных уравнений. [149] В 1936 году Алан Тьюринг публикует книгу « О вычислимых числах в приложении к Entscheidungsproblem ». [150] [примечание 106] Джон фон Нейман , пионер цифровых компьютеров и информатики, [примечание 107] в 1945 г., пишет неполное Первый проект отчета о EDVAC . В 1962 году Кеннет Э. Айверсон разработал нотацию составных частей, которая стала APL , для управления массивами, которую он обучал своих студентов и описал в своей книге «Язык программирования» . В 1970 году Эдгар Ф. Кодд предложил реляционную алгебру в качестве реляционной модели данных для языков запросов к базам данных . В 1971 году Стивен Кук издает « Сложность теоремы процедур , доказывающие » [151] В 1970е годырамках компьютерной архитектуры , Quote обозначениебыл разработан для представительной системы счисления рациональных чисел . Также в этом десятилетии в нотации Z (точно так же, как и в языке APL , задолго до него) используется множество символов, отличных от ASCII , спецификация включает предложения по отображению символов нотации Z в ASCII и LaTeX . В настоящее время существуют различные математические функции C (Math.h) и числовые библиотеки . Это библиотеки, используемые при разработке программного обеспечения для выполнения численных расчетов. Эти вычисления могут выполняться символическим исполнением.; анализ программы, чтобы определить, какие входные данные вызывают выполнение каждой части программы. Mathematica и SymPy - это примеры вычислительных программ, основанных на символической математике .
Будущее математической записи [ править ]
В истории математической нотации нотация идеографических символов прошла полный цикл с появлением компьютерных систем визуализации. Обозначения могут быть применены к абстрактной визуализации, например, для рендеринга некоторых проекций Калаби-Яу многообразии . Примеры абстрактной визуализации, которые принадлежат математическому воображению, можно найти в компьютерной графике . Потребность в таких моделях изобилует, например, когда меры объекта исследования на самом деле являются случайными величинами, а не обычными математическими функциями .
См. Также [ править ]
- Основная актуальность
- Злоупотребление обозначениями , Правильная формула , Нотация Big O ( L-нотация ), Нотация Даукера , Венгерская нотация , Инфиксная нотация , Позиционная нотация , Польская нотация ( Обратная польская нотация ), Знаковая нотация , История написания чисел
- Цифры и количества
- Список чисел , Иррациональные и предполагаемые иррациональные числа , γ , ζ (3) , √ 2 , √ 3 , √ 5 , φ , ρ , δ S , α , e , π , δ , Физические константы , c , ε 0 , h , G , греческие буквы, используемые в математике, науке и технике.
- Общая актуальность
- Порядок операций , научная запись ( инженерная запись ), актуарная запись
- Точечная запись
- Химическая нотация ( точечная нотация Льюиса ( электронная точечная нотация )), десятичная точка
- Обозначение стрелки
- Нотация Кнута, направленная вверх , бесконечная комбинаторика (Нотация стрелки (теория Рамсея))
- Геометрии
- Проективная геометрия , Аффинная геометрия , Конечная геометрия
- Списки и наброски
- Структура математики ( темы истории математики и математика темы ( Математика категория )), математических теории ( теории первого порядка , теоремы и опровергнут математические идеи ), математические доказательства ( Неполные Доказательства ), математические тождества , математические ряды , справочные таблицы Математика , Математическая логика темы , Математические методы , Математические функции , Преобразования иОператоры , Точки в математике , Математические фигуры , Узлы ( простые узлы и математические узлы и связи ), Неравенства , Математические концепции, названные в честь мест, Математические темы в классической механике , Математические вопросы в квантовой теории , Математические вопросы в теории относительности , Темы теории струн , Неразрешенные задачи по математике , математический жаргон , математические примеры , математические сокращения , список математических символов
- Разное.
- Проблемы Гильберта , математическое совпадение , шахматы обозначение , линия обозначение , нотная запись ( пунктирная примечание ), Whyte обозначение , Dice обозначение , рекурсивный категорический синтаксис
- Люди
- Математики ( любительские математики и женские математики ), Брадвардин , Томас Харриет , Хаусдорф , Гастон Жюлиа , Хельге фон Кох , Пауль Леви , Ляпунов , Бенуа Мандельброт , Льюис Фрай Ричардсон , Серпинский , Маклейн , Пол Коэн , Фрег , GS Carr , Robert Recorde , Bartel Leendert van der Waerden ,Харди , Э.М. Райт , Джеймс Р. Ньюман , Карл Густав Джейкоб Якоби , Роджер Джозеф Боскович , Эрик В. Вайсштейн , математические вероятностники , статистики
Примечания [ править ]
- ^ Или средневековье.
- ^ Фактически, такие символы сохранились с небольшими изменениями в римской системе обозначений , описание которых можно найти в«Философии арифметики» Джона Лесли .
- ^ Теория чисел - это раздел чистой математики, посвященный в первую очередь изучению целых чисел . Теоретики чисел изучают простые числа, а также свойства объектов, составленных из целых чисел (например, рациональных чисел ) или определенных как обобщения целых чисел (например, алгебраических целых чисел ).
- ^ Греческий : μή μου τοὺς κύκλους τάραττε
- ^ То есть.
- ^ Величина (математика) , относительный размер объекта; Величина (вектор) , термин, обозначающий размер или длину вектора; Скаляр (математика) , величина, определяемая только своей величиной; Евклидов вектор , величина, определяемая как величиной, так и направлением; Порядок величины , класс шкалы, имеющий отношение фиксированного значения к предыдущему классу.
- ^ Автолик " О Moving сферы является другой древней математической рукописью времени.
- ↑ Прокл , греческий математик, живший через несколько столетий после Евклида, написал в своем комментарии к Элементам: «Евклид, который собрал воедино элементы, собрал многие изтеорем Евдокса , усовершенствовал многие из теорем Теэтета , а также довел до исчерпывающего доказательстватеоремы.вещи, которые его предшественники лишь несколько слабо доказали ".
- ^ Выражение:будет записано как:SS2 C3 x5 M S4 u6. [ необходима цитата ]
- ^ такие как линейка , угольник , циркуль , уровень воды ( тростниковый уровень ) и отвес .
- ^ такие как колесо и ось
- ^ Площадь квадрата, описанного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, описанных на сторонах
- ↑ Аль-Кинди также ввел криптоанализ и частотный анализ .
- ^ Нечто близкое к доказательству с помощью математической индукции появляется в книге, написанной Аль-Караджи около 1000 г. н.э., который использовал ее для доказательства биномиальной теоремы , треугольника Паскаля и суммы целых кубов .
- ^ Таким образомон был близок к нахождению общей формулы для интегралов от полиномов, но он не был связан с любыми полиномами выше четвертой степени.
- ^ книга о том, что он считал недостатками в Элементах Евклида , особенно о параллельном постулате
- ^ переведен на латынь Робертом Честерским
- ^ переведены в различных версиях Аделардом Бата , Германом Каринтии и Герардом Кремоны
- ^ Его личное использование началось около 1351 года.
- ^ Summa de Arithmetica: Geometria Proportioni et Proportionalita. Тр . Сумма арифметики: геометрия в пропорциях и соразмерности.
- ↑ Большая часть работ принадлежит Пьеро Делла Франческа, которого он присвоил и украл .
- ^ Это был частный случай методов, данных много веков спустя Руффини и Хорнером .
- ^ То есть.
- ^ Потому что, как думают, он напоминал строчную букву «r» (от « radix »).
- ^ Опубликовано в Описание чудесного канона логарифмов
- ^ То есть∷
- ^ см. Закон непрерывности .
- ^ Используя декартовы координаты на плоскости, расстояние между двумя точками ( x 1 , y 1 ) и ( x 2 , y 2 ) определяется по формуле:
которую можно рассматривать как версию теоремы Пифагора .
- ^ Дальнейшие шаги в абстракции были предприняты Лобачевским , Бойяи , Риманом и Гауссом, которые обобщили концепции геометрии для разработки неевклидовых геометрий .
- ^ Теперь называется треугольником Паскаля .
- ^ Например, « проблема очков ».
- ^ То есть.
- ^ Например,
- ^ Оригинальное название, " De ratiociniis в Людо aleae "
- ^ Например, производная функции x будет записана как. Вторая производная от x будет записана каки т. Д.
- ^ Например, производная функции x по переменной t в обозначениях Лейбница будет записана как.
- ^ То есть.
- ^ См. Также: Список представлений е
- ^ Таким образомобозначает математический результат выполнения операциинад субъектом . Если бы после этого результата была повторена та же операция, новый результат был бы выражен, или, более кратко, и так далее. Сама величинарассматривается как результат той же операциинад некоторой другой функцией; правильный символкоторый, по аналогии. Таким образом,иявляются символами обратных операций , причем первые отменяют влияние вторых на объект. ианалогичным образом называются обратными функциями .
- ^ То есть
- ^ То есть
- ^ Сегодня символ, созданный Джоном Уоллисом ,используется дляобозначениябесконечности.
- ^ Как в,
- ^ Обозначение заглавной сигмы использует символ, который компактно представляет собой суммирование многих похожих терминов: символ суммирования , ∑ , увеличенная форма прямой заглавной греческой буквы сигма . Это определяется как:
Где, i представляет собой индекс суммирования ; a i - индексированная переменная, представляющая каждый последующий член в ряду; m - нижняя граница суммирования , а n - верхняя граница суммирования . «Я = т» под знаком суммы средств , что индекс я начинаю равен м . Индекс i увеличивается на 1 для каждого последующего члена, останавливаясь, когда i = n .
- ^ То есть. действительно для n> 0.
- ^ То есть∝
- ^ Пропорциональность - это отношение одной величины к другой, особенно отношение части к целому. В математическом контексте пропорция - это утверждение равенства между двумя отношениями; См. Пропорциональность (математика) , отношение двух переменных, отношение которых является постоянным. См. Также соотношение сторон , геометрические пропорции.
- ^ Фигурная д или дельта - Якоби .
- ^ О доказательстве теоремы Вильсона . Disquisitiones Arithmeticae (1801) Статья 76.
- ^ Теория Галуа и геометрия Галуа названаего честь.
- ^ То есть «подмножество» и «надмножество»; Позднее Эрнст Шредер переработал его.
- ^ Наука чисел , которая использует методы из математического анализа для решения задач о целых числах.
- ^ Цитируется в Роберте Персевале Грейвсе " Жизнь сэра Уильяма Роуэна Гамильтона" (3 тома, 1882, 1885, 1889)
- ^ То есть(или, позже названный del , ∇)
- ^ См. Гамильтониан (квантовая механика) .
- ^ То есть i 2 = j 2 = k 2 = i j k = − 1 {\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1}
- ^ Хотя его использование описывает нечто иное, чем то, что сейчас подразумевается под тензором. А именно, операция нормы в определенном типе алгебраической системы (теперь известной как алгебра Клиффорда ).
- ^ То естьгде
- ^ Это латинское слово "матка".
- ^ То есть q = w + x i + y j + z k {\displaystyle q=w+xi+yj+zk}
- ^ Клиффорд пересек алгебру с кватернионами Гамильтона, заменивправило Германа Грассмана e p e p = 0 правилом e p e p = 1. Подробнее см. Внешняя алгебра .
- ^ См .: Фазор , Группа (математика) , Скорость сигнала , Многофазная система , Гармонический осциллятор и последовательная цепь RLC.
- ^ Или концепция четвертого пространственного измерения. См. Также: Пространство- время, объединение времени и пространства как четырехмерного континуума ; и пространство Минковского , математическое обоснование специальной теории относительности.
- ^ См. Также: Математические поля и расширение поля
- ^ Комментарий после доказательства того, что 1 + 1 = 2, завершенного в Principia mathematica, Альфредом Норт Уайтхедом ... и Бертраном Расселом. Том II, первое издание (1912 г.)
- ^ Это поднимает вопросы о чистых теоремах существования .
- ^ Formulario Mathematico Пеано, хотя и менее популярный, чем работа Рассела, выдержал пять изданий. Пятый появился в 1908 году и включал 4200 формул и теорем.
- ^ Изобретатель теории множеств
- ^ Трансфинитная арифметика - это обобщение элементарной арифметики на бесконечные величины, такие как бесконечные множества ; См. Разделы Трансфинитные числа , Трансфинитная индукция и Трансфинитная интерполяция . См. Также Порядковая арифметика .
- ^ Такие, как Макс Ден , Дж. В. Александр и другие.
- ^ Например, полином Александра .
- ^ (Немецкий: алгебраическая теория дер Кёрпер)
- ^ В этой статье Стейниц аксиоматически изучал свойства полей и определил много важной области теоретических концепцийкак простое поле , совершенное поле и степень трансцендентности в виде расширения поля .
- ^ Индексы пробегает множество {1, 2, 3} ,
уменьшаются на конвенцию:
Верхние индексы не являются показателями , но индексы координат, коэффициентов или базисных векторов .
Смотрите также: исчисление Риччи
- ^ Исчисление Риччи составляет правила обозначения индексов и манипуляций с тензорами и тензорными полями . См. Также: Synge JL; Шильд А. (1949). Тензорное исчисление . первое издание Dover Publications 1978 года. С. 6–108.
- ^ Здесь логическая константа - это символ в символьной логике, который имеет одинаковое значение во всех моделях, например, символ «=» для «равно». Константа , в математическом контексте, это число , которое естественным образом возникает в области математики , такие как ялибо е; В такой математике постоянные значения не меняются. Это может означать полиномиальный постоянный член (член степени 0) или постоянную интегрирования , свободный параметр, возникающий при интегрировании.Связанные с этим физические константы - это физическая величина, которая обычно считается универсальной и неизменной. Константы программирования
- это значения, которые, в отличие от переменной, не могут быть повторно связаны с другим значением. - ^ Хотя это и не индексный термин , ключевые слова - это термины, которые представляют информацию. Ключевое слово - это слово со специальным значением (это семантическое определение), а синтаксически это терминальные символы в грамматике фраз. См. Зарезервированное слово для соответствующей концепции.
- ^ Большинство этих символов можно найти в исчислении высказываний , формальной системе, описываемой как. - это набор элементов, таких как a в приведенном выше примере с булевой алгеброй. - это набор, содержащий подмножества, содержащие операции, такие какили. содержит правила вывода , которые являются правилами, определяющими, как выводы могут быть логически сделаны, исодержит аксиомы . См. Также: Базовые и производные формы аргументов .
- ^ Обычно обозначаетсябуквами x , y , z или другими строчными буквами.
Здесь символы, представляющие величину в математическом выражении, математическую переменную, используемую во многих науках.
Переменные могут иметь символическое имя, связанное со значением, связанное с которым значение может быть изменено, известное в информатике как ссылка на переменную . Переменный может также быть в действие способомв котором атрибут представлен для дальнейшей обработки данных (например, логический набор атрибутов). См. Также: Зависимые и независимые переменные в статистике. - ^ Обычно обозначается прописной буквой, за которой следует список переменных, например P ( x ) или Q ( y , z ).
Здесь предикат математической логики , фундаментальное понятие в логике первого порядка. Грамматические предикаты - это грамматические компоненты предложения.
Связан синтаксический предикат в технологии синтаксического анализа, который является руководством для процесса синтаксического анализа. В компьютерном программировании предсказание ветвления позволяет выбирать выполнять или не выполнять данную инструкцию на основе содержимого машинного регистра. - ^ Представляя ВСЕ и СУЩЕСТВУЕТ
- ^ например, ∃ для "существует" и ∀ для "для всех"
- ^ Смотрите также: Dialetheism , Противоречие и Paradox
- ^ Связанная, шутливая абстрактная бессмыслица описывает определенные виды аргументов и методов, относящихся к теории категорий, которые напоминают комические литературные приемы non sequitur (не нелогичные non sequiturs ).
- ^ Теоремы Гёделя о неполноте показывают, что программа Гильберта по поиску полного и непротиворечивого набора аксиом для всей математики невозможна, что дает оспариваемый отрицательный ответ на вторую проблему Гильберта
- ^ Например, возьмем утверждение «Существует такое число x , которое не является y ». Использование символов исчисления высказываний, это стало бы: .
Если число Геделя заменить символы, она становится:. Есть десять чисел, так что десять простых числа найдены и это:. Затем число Геделя сделаны полномочия соответствующих простых чисел и умножается,дает:. Полученное число примерно.
- ^ Уравнение Клейна – Гордона:
- ^ Уравнение Дирака в форме, первоначально предложенной Дираком:
где ψ = ψ ( х , т ) является волновая функция для электрона , х и т являются пространственные и временные координаты, т есть масса покоя электрона, р представляет собой импульс , понимается как оператор импульса в Теория Шредингера , c - скорость света , а ħ = h / 2 π - приведенная постоянная Планка . - ^ То есть
- ^ Теорема применима в более общем плане к любой достаточно сильной формальной системе, показывая, что истина в стандартной модели системы не может быть определена внутри системы.
- ↑ Назван в честь работы Фойгта 1898 года.
- ^ Назван в честь Артура Морица Шенфлиса
- ^ См. Связи Галуа .
- ^ Ойстейн Оре также написал бы « Теорию чисел и ее историю ».
- ^
- ^ Что амплитуду рассеяния можно рассматривать как аналитическую функцию углового момента, и что положение полюсов определяет степенные темпы роста амплитуды в чисто математической области больших значений косинуса угла рассеяния.
- ^ То есть
- ^ Также известен как Даламбертиан или волновой оператор .
- ^ Также известен как « символ перестановки » (см .: перестановка ), « антисимметричный символ » (см .: антисимметричный ) или « переменный символ »
- ^ Отметимчто « массы » (например, когерентное не определенная форма тела) частиц периодически переоцениваются по научным сообществом . Значения могли быть скорректированы; регулировка с помощью операций, выполняемых с приборами, для обеспечения заданных показаний, соответствующих заданным значениям измеряемой величины. В технике, математике и геодезии, оптимальный параметр такая оценка в математической модели так, чтобы наилучшим образом соответствует в набор данных .
- ^ Для консенсуса см. Группа данных по частицам .
- ^ Локально определенный набор из четырех линейно независимых векторных полей, называемый тетрадой
- ^ Его использование суммирования Эйнштейна было для того, чтобы компенсировать неудобство при описании сокращений и ковариантного дифференцирования в современной абстрактной тензорной нотации, сохраняя при этом явную ковариантность используемых выражений.
- ^ См. Также: Пейзаж теории струн и Болото
- ^ Предназначенный от Джошуа Ледербергом дополненной Кокстером и Фрухта
- ^ И в 1938 году Тьюринг AM (1938). «О вычислимых числах в приложении к Entscheidungsproblem. Исправление». Труды Лондонского математического общества . s2-43: 544–546. DOI : 10.1112 / ПНИЛИ / s2-43.6.544 ..
- ↑ Среди других работ фон Неймана - применение теории операторов к квантовой механике , в развитие функционального анализа и к различным формам теории операторов .
Ссылки и цитаты [ править ]
- Общий
- Флориан Каджори (1929) История математических обозначений , 2 тома. Отпечаток Dover в 1 томе, 1993. ISBN 0-486-67766-4 .
- Цитаты
- ↑ Флориан Каджори . История математических обозначений: два тома в одном. Cosimo, Inc., 1 декабря 2011 г.
- ^ Словарь науки, литературы и искусства, Том 2. Под редакцией Уильяма Томаса Бранда , Джорджа Уильяма Кокса . Стр. 683
- ^ "Обозначение - из Wolfram MathWorld" . Mathworld.wolfram.com . Проверено 24 июня 2014 .
- ^ Диофант Александрийский: Исследование по истории греческой алгебры. Сэр Томас Литтл Хит. Pg 77 .
- ^ Математика: его сила и полезность. Карл Дж. Смит. Pg 86 .
- ^ Коммерческая революция и начало западной математики в эпоху Возрождения Флоренция, 1300–1500. Уоррен Ван Эгмонд. 1976. С. 233.
- ^ Соломон Гандз . «Источники алгебры аль-Ховаризми»
- ↑ Энциклопедия Американа. Томас Гамалиэль Брэдфорд. Стр. 314
- ^ Математический экскурс, Расширенное издание: Расширенное издание Webassign Ричард Н. Ауфманн, Джоан Локвуд, Ричард Д. Нэйшн, Дэниел К. Клег. Страница 186
- ^ Математика в Египте и Месопотамии [ мертвая ссылка ]
- ^ Бойер, CB История математики , 2-е изд. rev. пользователя Uta C. Merzbach . Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). «Месопотамия» с. 25.
- ^ Дункан Дж. Мелвилл (2003). Третья хронология тысячелетия , Третья Mathematics тысячелетия . Университет Святого Лаврентия .
- ^ Aaboe, Аскер (1998). Эпизоды из ранней истории математики . Нью-Йорк: Random House. С. 30–31.
- ^ Хит (1931). «Учебное пособие по греческой математике». Природа . 128 (3235): 5. Bibcode : 1931Natur.128..739T . DOI : 10.1038 / 128739a0 . S2CID 3994109 .
- ↑ Сэр Томас Л. Хит, Руководство по греческой математике , Дувр, 1963, стр. 1: «В случае математики наиболее важно знать вклад Греции, поскольку именно греки сделали математику наукой».
- ^ a b Новая энциклопедия; или Универсальный словарь искусств и наук. Энциклопедия Perthensi. Стр. 49
- ^ Calinger, Рональд (1999). Контекстная история математики . Прентис-Холл. п. 150. ISBN 0-02-318285-7.
Вскоре после Евклида, составителя окончательного учебника, пришел Архимед Сиракузский (ок. 287 212 до н.э.), самый оригинальный и глубокий математик древности.
- ^ "Архимед Сиракузский" . Архив истории математики MacTutor. Январь 1999 . Проверено 9 июня 2008 года .
- ^ О'Коннор, JJ; Робертсон, EF (февраль 1996 г.). «История математического анализа» . Сент-Эндрюсский университет . Архивировано 15 июля 2007 года . Проверено 7 августа 2007 года .
- ^ "Резюме Прокла" . Gap.dcs.st-and.ac.uk. Архивировано из оригинального 23 сентября 2015 года . Проверено 24 июня 2014 .
- ↑ Колдуэлл, Джон (1981) « Институт арифметики и институт музыки », стр. 135–54 в издании Маргарет Гибсон, Боэций: его жизнь, мысли и влияние (Оксфорд: Бэзил Блэквелл).
- ^ Фолкертс, Menso, "Боэций" Geometrie II , (Wiesbaden: Franz Steiner Verlag, 1970).
- ^ Математика и измерения Освальда Эштона Вентворта Дилка. Стр. 14
- ^ а б в г д Научно-литературный и художественный словарь под ред. пользователя WT Brande. Стр. 683
- ^ Бойер, Карл Б. История математики , 2-е издание, John Wiley & Sons, Inc., 1991.
- ^ Диофантовы уравнения . Представлено: Аароном Церхузеном, Крисом Рейксом и Шастой Мис. МА 330-002. Доктор Карл Эберхарт. 16 февраля 1999 г.
- ^ История греческой математики: от Аристарха до Диофанта. Сэр Томас Литтл Хит. Стр. 456
- ^ История греческой математики: от Аристарха до Диофанта. Сэр Томас Литтл Хит. Стр. 458
- ^ The American Mathematical Monthly, том 16. Стр. 131
- ^ «Обзор китайской математики» . Groups.dcs.st-and.ac.uk . Проверено 24 июня 2014 .
- ^ Джордж Gheverghese Джозеф, The Crest павлина: неевропейские корни математики , Penguin Books, London, 1991, pp.140-148
- ^ Georges Ифра, Universalgeschichte дер Zahlen , Campus, Frankfurt / НьюЙорк, 1986, pp.428-437
- ^ "Фрэнк Дж. Свец и Т.И. Као: Был ли Пифагор китайцем?" . Psupress.psu.edu . Проверено 24 июня 2014 .
- ^ a b Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о Небесах и Земле. Тайбэй: Caves Books, Ltd.
- ^ Сэл Рестиво
- ^ Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о Небесах и Земле. Тайбэй: Caves Books, Ltd.
- ^ Марсель Гоше , 151.
- ^ Бойер, CB История математики, 2-е изд. rev. пользователя Uta C. Merzbach. Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). «Китай и Индия» с. 221. (ср., «Он был первым, кто дал общее решение линейного диофантова уравнения ax + by = c, где a, b и c - целые числа. [...] Это большая заслуга Брахмагупта, что он отдал все интегральные решения линейного диофантова уравнения, тогда как сам Диофант удовлетворился тем, что дал одно частное решение неопределенного уравнения. Поскольку Брахмагупта использовал некоторые из тех же примеров, что и Диофант, мы снова видим вероятность греческого влияния в Индии - или возможность того, что они оба использовали общий источник, возможно, из Вавилонии. Интересно также отметить, что алгебра Брахмагупты, как и алгебра Диофанта, была синкопирована. Сложение обозначалось сопоставлением, вычитание - помещением точки над вычитаемым, а деление - помещением делителя под делимым, как в нашей дробной системе счисления, но без черты. Операции умножения и эволюции (извлечения корней), а также неизвестные величины были представлены сокращениями соответствующих слов. ")
- ^ Роберт Каплан, "Ничто, что есть: естественная история нуля", Аллен Лейн / Penguin Press, Лондон, 1999
- ^ " " Гениальный метод выражения всех возможных чисел с помощью набора из десяти символов (каждый символ имеет разрядное значение и абсолютное значение) появился в Индии. В наши дни идея кажется настолько простой, что ее значимость и глубокая важность больше не осознаются. Его простота заключается в том, что он упрощает вычисления и ставит арифметику на первое место среди полезных изобретений. важность этого изобретения легче понять, если учесть, что оно превосходило двух величайших людей Античности, Архимеда и Аполлония »- Пьер-Симон Лаплас» . History.mcs.st-and.ac.uk . Проверено 24 июня 2014 .
- ^ AP Juschkewitsch , "Geschichte дер Mathematik им Mittelalter", Teubner, Лейпциг, 1964
- ^ Бойер, CB История математики, 2-е изд. rev. пользователя Uta C. Merzbach. Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). «Арабская гегемония» с. 230. (см. «Шесть случаев приведенных выше уравнений исчерпывают все возможности для линейных и квадратных уравнений, имеющих положительный корень. Изложение аль-Хваризми было настолько систематическим и исчерпывающим, что его читатели, должно быть, не испытывали особых трудностей в освоении решений»).
- ^ Gandz и Саломаны (1936), Источники алгебры Хореой , Осирис я, стр 263-77:. «В некотором смысле, Хорезй более право называться„отец алгебры“чемДиофантпотому что Хорезй является первымчтобы научить алгебры в элементарной форме и ради нее самого Диофанта занимается прежде всего теорией чисел ».
- ^ Бойер, CB История математики, 2-е изд. rev. пользователя Uta C. Merzbach. Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). «Арабская гегемония» с. 229. (ср., «Не совсем ясно, чтоозначаюттермины аль-джабр и мукабала , но обычное толкование аналогично тому, что подразумевается в переводе выше. Слово аль-джабр предположительно означало что-то вроде« восстановление »или« завершение »и, кажется, относится к переносу вычитаемых членов на другую сторону уравнения; слово мукабала, как говорят, относится к« сокращению »или« уравновешиванию », то есть
- ^ Rashed, R .; Армстронг, Анджела (1994). Развитие арабской математики . Springer . С. 11–12. ISBN 0-7923-2565-6. OCLC 29181926 .
- ↑ Виктор Дж. Кац (1998). История математики: Введение , стр. 255–59. Эддисон-Уэсли . ISBN 0-321-01618-1 .
- ^ F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi . Париж.
- ^ Кац, Виктор Дж. (1995). «Идеи исчисления в исламе и Индии». Математический журнал . 68 (3): 163–74. DOI : 10.1080 / 0025570X.1995.11996307 .
- ^ Kunitzsch, Пол (2003), "О передаче индо-арабскими цифрами Пересмотренные" , в JP Hogendijk; А.И. Сабра (ред.), Предприятие науки в исламе: новые перспективы , MIT Press, стр. 3–22 (12–13), ISBN 978-0-262-19482-2
- ^ Мари-Терез d'Alverny, «Переводы и переводчики», стр 421-62 в Роберт Л. Бенсон и Giles констебль,. Ренессанс и обновлении в двенадцатом веке , (Кембридж: Harvard University Press, 1982).
- ^ Г Beaujouan, «Трансформация Quadrivium», стр 463-87 в Роберт Л. Бенсон и Giles констебль,. Ренессанс и обновлении в двенадцатом веке , (Кембридж: Harvard University Press, 1982).
- ^ О'Коннор, Джон Дж .; Робертсон, Эдмунд Ф. , "аль-Марракуши ибн аль-Банна" , архив истории математики MacTutor , Университет Сент-Эндрюс.
- ^ Гуллберг, Ян (1997). Математика: от рождения чисел . WW Нортон. п. 298 . ISBN 0-393-04002-X.
- ^ а б О'Коннор, Джон Дж .; Робертсон, Эдмунд Ф. , «Абу'л Хасан ибн Али аль-Каласади» , архив истории математики MacTutor , Университет Сент-Эндрюс.
- ^ Бойер, CB История математики, 2-е изд. rev. пользователя Uta C. Merzbach. Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). «Возрождение и упадок греческой математики» с. 178 (ср. «Основное отличие диофантова синкопа от современной алгебраической записи - отсутствие специальных символов для операций и отношений, а также экспоненциальной записи»).
- ^ Грант, Эдвард и Джон Э. Мердок (1987), редакторы, Математика и ее приложения к науке и естественной философии в средние века , (Кембридж: издательство Кембриджского университета) ISBN 0-521-32260-X .
- ^ Математический журнал, Том 1. Артемас Мартин, 1887. Pg 124.
- ^ Der Algorismus ratio des Nicolaus Oresme : Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Николь Орем . С. Голгофа и компания, 1868 г.
- ^ Clagett, Маршалл (1961) Наука механики в средние века (Мэдисон: Университет Висконсин Press), стр 332-45, 382-91..
- ^ Более поздняя ранняя современная версия : Новая система товарной арифметики : адаптирована к торговле Соединенных Штатов, в ее внутренних и внешних отношениях с формами счетов и другими письменными документами, обычно встречающимися в торговле. По Майкл Уолш . Эдмунд М. Блант (владелец), 1801 г.
- ↑ Миллер, Джефф (4 июня 2006 г.). «Раннее использование символов операций» . Средняя школа Персидского залива . Проверено 24 сентября 2006 года .
- ^ Арифметические книги от изобретения печати до наших дней. Автор Огастес Де Морган . стр 2 .
- Перейти ↑ Grattan-Guinness, Ivor (1997). Радуга математики: история математических наук . WW Нортон. ISBN 0-393-32030-8.
- ^ Arithmetica Integra . По Михаэль Штифель , Philipp Меланхтона . Norimbergæ : Apud Iohan Petreium , 1544.
- ^ История математики Энн Роун. Стр. 40
- ↑ Мемуары Джона Напьера из Мерчистона . Марк Напье
- ↑ Отчет о жизни, сочинениях и изобретениях Джона Напьера из Мерчистона . Дэвид Стюарт Эрскин, граф Бьюкен, Уолтер Минто
- ↑ Флориан Каджори (1919). История математики . Макмиллан. п. 157 .
- ^ Ян Гуллберг , Математика с момента рождения чисел, WW Norton & Company; ISBN 978-0-393-04002-9 . стр. 963–965,
- ^ Сводка Palmariorum Matheseos . По Уильяма Джонса . 1706. ( Альтернативный вариант : Synopsis Palmariorum Matheseos: или Новое введение в математику . Archive.org.)
- ^ Когда меньше значит больше: визуализация основных неравенств. Клауди Альсина, Роджер Б. Нелсе. Pg 18 .
- ^ Эйлер, Леонард, Solutio problematis ad geometriam situs pertinentis
- ^ Элементы геометрии . Уильям Эмерсон
- ^ Доктрина пропорции, арифметической и геометрической. Вместе с общим методом пропорционального распределения . Уильям Эмерсон.
- ^ Математический корреспондент. Джордж Барон. 83
- ^ Vitulli, Мари . «Краткая история линейной алгебры и теории матриц» . Кафедра математики . Университет Орегона. Архивировано из оригинального 10 сентября 2012 года . Проверено 24 января 2012 года .
- ^ "Биография Крампа" . History.mcs.st-and.ac.uk . Проверено 24 июня 2014 .
- ^ Mécanique analytique: Том 1 , Том 2 . По Жозеф Луи Лагранж . Мисс Ве Курсье , 1811 год.
- ^ Собрание математических работ Артура Кэли . Том 11. Страница 243 .
- ^ Историческая энциклопедия естественных и математических наук, том 1. Ари Бен-Менахем. Стр. 2070 .
- ^ Vitulli, Мари . «Краткая история линейной алгебры и теории матриц». Кафедра математики. Университет Орегона. Первоначально по адресу: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html.
- ^ Слова математики. Стивен Шварцман. 6 .
- ^ Электро-магнетизм: теория и приложения. Автор А. Праманик. 38
- ^ История Наблы и других математических символов . homepages.math.uic.edu/~hanson.
- ^ Гамильтон, Уильям Роуэн (1854–1855). Уилкинс, Дэвид Р. (ред.). «О некоторых расширениях кватернионов» (PDF) . Философский журнал (7–9): 492–499, 125–137, 261–269, 46–51, 280–290. ISSN 0302-7597 .
- ^ "Джеймс Клерк Максвелл" . Сеть глобальной истории IEEE . Проверено 25 марта 2013 года .
- ^ Максвелл, Джеймс Клерк (1865). «Динамическая теория электромагнитного поля» (PDF) . Философские труды Лондонского королевского общества . 155 : 459–512. Bibcode : 1865RSPT..155..459C . DOI : 10,1098 / rstl.1865.0008 . S2CID 186207827 . (Эта статья сопровождала выступление Максвелла 8 декабря 1864 г. перед Королевским обществом.)
- ↑ Книги I, II, III (1878 г.) в Интернет-архиве ; Книга IV (1887 г.) в Интернет-архиве
- ^ Кокс, Дэвид А. (2012). Теория Галуа . Чистая и прикладная математика. 106 (2-е изд.). Джон Вили и сыновья. п. 348. ISBN 978-1118218426.
- ^ "TÜBİTAK ULAKBİM DergiPark" . Journals.istanbul.edu.tr. Архивировано из оригинального 16 марта 2014 года . Проверено 24 июня 2014 .
- ^ "Линейная алгебра: Хусейн Тевфик: Бесплатная загрузка и потоковая передача: Интернет-архив" . А. Х. Бояджян. +1882 . Проверено 24 июня 2014 .
- ^ Риччи Курбастро, Г. (1892). "Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique". Bulletin des Sciences Mathématiques . 2 (16): 167–189.
- Перейти ↑ Voigt, Woldemar (1898). Die Fundmentalen Physikalischen Eigenschaften der Krystalle в elementarer Darstellung . Лейпциг: фон Файт.
- ↑ Пуанкаре, Анри, "Analysis situs", Journal de l'École Polytechnique ser 2, 1 (1895), стр. 1–123
- ^ Уайтхед, Джон Б., младший (1901). «Обзор: Явления переменного тока , автор CP Steinmetz» (PDF) . Бык. Амер. Математика. Soc . 7 (9): 399–408. DOI : 10.1090 / s0002-9904-1901-00825-7 .
- ^
Есть много редакций. Вот два:
- (Французский) Опубликовано в 1901 году Готье-Вилларом, Париж. 230p. OpenLibrary OL15255022W , PDF .
- (Итальянский) Опубликовано в 1960 году издательством Edizione cremonese, Roma. 463п. OpenLibrary OL16587658M .
- ^ Риччи, Грегорио ; Леви-Чивита Туллио (март 1900 г.), "Méthodes де Расчитать différentiel Absolu и др Leurs приложения" , Mathematische Annalen , Springer, 54 (1-2): 125-201, DOI : 10.1007 / BF01454201 , S2CID 120009332
- ↑ Цермело, Эрнст (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (перепечатка) . Mathematische Annalen . 59 (4): 514–16. DOI : 10.1007 / BF01445300 . S2CID 124189935 .
- ↑ - через Wikisource .
- ^ Фреше, Морис, "Sur quelques points du Calcul fonctionnel", докторская диссертация, 1906 г.
- ↑ Катберт Эдмунд Каллис (автор) (5 июня 2011 г.). "Матрицы и детереноиды Том 2: Катберт Эдмунд Каллис: Amazon.com: Книги" . Проверено 24 июня 2014 .
- ^ Может быть назначена заданная матрица : О классе матриц. (Gr. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) Исай Шур
- ^ Введение в современную теорию уравнений . Флориан Каджори.
- ^ Труды Прусской академии наук (1918). Стр.966.
- ^ Sitzungsberichte дер Preussischen Akademie дер Wissenschaften (1918) (Tr. Труды Прусской Академии наук (1918)). archive.org; См. Также: Теория Калуцы – Клейна .
- ^ Дж. А. Уиллер; К. Миснер; К.С. Торн (1973). Гравитация . WH Freeman & Co. стр. 85 -86, § 3.5. ISBN 0-7167-0344-0.
- ^ Р. Пенроуз (2007). Дорога к реальности . Винтажные книги. ISBN 978-0-679-77631-4.
- ↑ Схоутен, Ян А. (1924). Р. Курант (ред.). Der Ricci-Kalkül - Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Исчисление Риччи - Введение в новейшие методы и проблемы многомерной дифференциальной геометрии) . Grundlehren der Mathematischen Wissenschaften (на немецком языке). 10 . Берлин: Springer Verlag.
- ^ Роберт Б. Эш. Учебник по абстрактной математике. Cambridge University Press, 1 января 1998 г.
- ^ Новый американский энциклопедический словарь. Под редакцией Эдварда Томаса Роу, Ле Роя Хукера, Томаса У. Хэндфорда. Стр. 34
- ^ Математические принципы естественной философии, Том 1. Сэр Исаак Ньютон, Джон Мачин. Стр.12.
- ^ В The Scientific Outlook (1931)
- ^ Математика упрощена и сделана привлекательной: или, объяснение законов движения. Томас Фишер. Стр. 15. (ср. Но абстракция, не основанная на Природе и ( Логической ) Истине и не согласная с ними , была бы ложью , безумием . )
- ^ Предложение VI, О формально неразрешимых предложениях в Principia Mathematica и родственных системах I (1931)
- ^ Касти, Джон Л. 5 Золотых правил . Нью-Йорк: MJF Books, 1996.
- ^ Gr. Methoden Der Mathematischen Physik
- ^ Дирак (1927). «Квантовая теория излучения и поглощения излучения» . Труды Королевского общества Лондона . 114 (767): 243–265. Bibcode : 1927RSPSA.114..243D . DOI : 10.1098 / RSPA.1927.0039 .
- ↑ Э. Ферми (1932). «Квантовая теория излучения». Обзоры современной физики . 4 (1): 87–132. Bibcode : 1932RvMP .... 4 ... 87F . DOI : 10.1103 / RevModPhys.4.87 .
- ^ Ф. Блох ; А. Нордсик (1937). «Заметка о радиационном поле электрона». Физический обзор . 52 (2): 54–59. Полномочный код : 1937PhRv ... 52 ... 54B . DOI : 10.1103 / PhysRev.52.54 .
- ↑ VF Weisskopf (1939). «О собственной энергии и электромагнитном поле электрона». Физический обзор . 56 (1): 72–85. Bibcode : 1939PhRv ... 56 ... 72W . DOI : 10.1103 / PhysRev.56.72 .
- ^ Р. Оппенгеймер (1930). «Заметка о теории взаимодействия поля и материи». Физический обзор . 35 (5): 461–477. Полномочный код : 1930PhRv ... 35..461O . DOI : 10.1103 / PhysRev.35.461 .
- ^ Ван дер Варден BL (1929). «Спиноранализ». Nachr. Ges. Wiss. Göttingen Math.-Phys . 1929 : 100–109.
- ↑ Веблен О. (1933). «Геометрия двухкомпонентных спиноров» . Proc. Natl. Акад. Sci. США . 19 (4): 462–474. Bibcode : 1933PNAS ... 19..462V . DOI : 10.1073 / pnas.19.4.462 . PMC 1086023 . PMID 16577541 .
- ^ Дирак (1939). «Новые обозначения для квантовой механики» . Математические труды Кембриджского философского общества . 35 (3). С. 416–418. Bibcode : 1939PCPS ... 35..416D . DOI : 10.1017 / S0305004100021162 .
- ^ Х. Грассманн (1862). Теория расширений . История источников математики. Американское математическое общество, Лондонское математическое общество, 2000 перевод Ллойда К. Канненберга.
- ^ Стивен Вайнберг (1964), Квантовая теория полей, Том 2 , Cambridge University Press, 1995, стр. 358, ISBN 0-521-55001-7
- ^ "Нобелевская премия по физике 1965" . Нобелевский фонд . Проверено 9 октября 2008 года .
- ↑ SL Glashow (1961). «Частичные симметрии слабых взаимодействий». Ядерная физика . 22 (4): 579–588. Bibcode : 1961NucPh..22..579G . DOI : 10.1016 / 0029-5582 (61) 90469-2 .
- ^ С. Вайнберг (1967). «Модель лептонов». Письма с физическим обзором . 19 (21): 1264–1266. Bibcode : 1967PhRvL..19.1264W . DOI : 10.1103 / PhysRevLett.19.1264 .
- ↑ А. Салам (1968). Н. Свартхольм (ред.). Физика элементарных частиц: релятивистские группы и аналитичность . Восьмой Нобелевский симпозиум . Стокгольм: Альмквист и Викселл . п. 367.
- ^ Ф. Энглерт; Р. Браут (1964). «Нарушенная симметрия и масса калибровочных векторных мезонов» . Письма с физическим обзором . 13 (9): 321–323. Bibcode : 1964PhRvL..13..321E . DOI : 10.1103 / PhysRevLett.13.321 .
- ^ PW Хиггс (1964). «Нарушенные симметрии и массы калибровочных бозонов» . Письма с физическим обзором . 13 (16): 508–509. Bibcode : 1964PhRvL..13..508H . DOI : 10.1103 / PhysRevLett.13.508 .
- ^ Г.С. Гуральник; CR Hagen; TWB Kibble (1964). «Глобальные законы сохранения и безмассовые частицы» . Письма с физическим обзором . 13 (20): 585–587. Bibcode : 1964PhRvL..13..585G . DOI : 10.1103 / PhysRevLett.13.585 .
- ^ http://www.physics.drexel.edu/~vkasli/phys676/Notes%20for%20a%20brief%20history%20of%20quantum%20gravity%20-%20Carlo%20Rovelli.pdf
- ^ Бурбаки, Николас (1972). «Универс» . В Майкле Артине ; Александр Гротендик ; Жан-Луи Вердье (ред.). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Конспект лекций по математике 269 ) (на французском языке). Берлин; Нью-Йорк: Springer-Verlag . С. 185–217.
- ^ FJ Hasert; и другие. (1973). «Поиски упругого рассеяния электронов мюон-нейтрино». Физика Письма Б . 46 (1): 121. Bibcode : 1973PhLB ... 46..121H . DOI : 10.1016 / 0370-2693 (73) 90494-2 .
- ^ FJ Hasert; и другие. (1973). «Наблюдение нейтриноподобных взаимодействий без мюона или электрона в нейтринном эксперименте Гаргамеля». Физика Письма Б . 46 (1): 138. Bibcode : 1973PhLB ... 46..138H . DOI : 10.1016 / 0370-2693 (73) 90499-1 .
- ^ FJ Hasert; и другие. (1974). «Наблюдение нейтриноподобных взаимодействий без мюона или электрона в нейтринном эксперименте Гаргамеля». Ядерная физика Б . 73 (1): 1. Bibcode : 1974NuPhB..73 .... 1H . DOI : 10.1016 / 0550-3213 (74) 90038-8 .
- ^ D. Haidt (4 октября 2004). «Открытие слабых нейтральных токов» . ЦЕРН Курьер . Проверено 8 мая 2008 года .
- ^ "Главная страница" .
- ^ Канделас, P. (1985). «Вакуумные конфигурации для суперструн». Ядерная физика Б . 258 : 46–74. Bibcode : 1985NuPhB.258 ... 46С . DOI : 10.1016 / 0550-3213 (85) 90602-9 .
- ^ Де Феличе, Ф .; Кларк, CJS (1990), Теория относительности на искривленных многообразиях , стр. 133
- ^ "Квантовые инварианты узлов и 3-многообразий" В. Г. Тураева (1994), стр. 71
- ^ Писанский, Томаж ; Серватиус, Бриджит (2013), «2.3.2 Кубические графы и нотация LCF», Конфигурации с графической точки зрения , Springer, стр. 32, ISBN 9780817683641
- ^ Frucht, R. (1976), «Каноническое представление трехвалентных гамильтоновых графов», Журнал теории графов , 1 (1): 45–60, DOI : 10.1002 / jgt.3190010111
- ^ Fraleigh 2002: 89; Хангерфорд 1997: 230
- ^ Ден, Эдгар. Алгебраические уравнения, Дувр. 1930: 19
- ^ "Ударник IBM 601 Умножающий" . Columbia.edu . Проверено 24 июня 2014 .
- ^ «Связанное оборудование перфокарт» . Columbia.edu. 24 октября 1935 . Проверено 24 июня 2014 .
- ^ Труды Лондонского математического общества 42 (2)
- ^ Кук, Стивен (1971). «Сложность процедур доказательства теорем» . Материалы третьего ежегодного симпозиума ACM по теории вычислений . С. 151–158.
Дальнейшее чтение [ править ]
- Общий
- Краткое изложение истории математики . По Вальтера Уильяма Рауза Бал .
- Букварь по истории математики . Уолтер Уильям Роуз Болл.
- История элементарной математики : с подсказками о методах обучения. Флориан Каджори.
- История элементарной математики . Флориан Каджори.
- История математики . Флориан Каджори.
- Краткая история греческой математики . По Джеймс Гоу .
- О развитии математической мысли в девятнадцатом веке . По Джон Теодор Мерц .
- Новый математико-философский словарь . Питер Барлоу.
- Историческое введение в математическую литературу . По Джордж Миллер Абрама
- Краткая история математики . По Карл Финк , Вустер Вудрафф Беман , Дэвид Юджин Смит
- История современной математики . Дэвид Юджин Смит.
- История современной математики . Дэвид Юджин Смит, Мэнсфилд Мерриман .
- Другой
- Principia Mathematica, Том 1 и Том 2 . Альфред Норт Уайтхед, Бертран Рассел.
- Математические основы естественной философии , том 1, выпуск 1. Сэр Исаак Ньютон, Эндрю Мотт, Уильям Дэвис, Джон Мачин, Уильям Эмерсон.
- Общие исследования криволинейных поверхностей 1827 и 1825 гг . Карл Фридрих Гаус.
Внешние ссылки [ править ]
- Математическая нотация: прошлое и будущее
- История математических обозначений
- Самые ранние виды использования математических обозначений
- Подсчет пальцев . files.chem.vt.edu.
- Некоторые общеупотребительные математические символы и сокращения (с историей) . Исайя Лэнкхэм, Бруно Нахтергаэле, Энн Шиллинг.

























![f [f (x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f54da4ffd78a97e0493340583f3157015327436)




























