Метод Лилля

Нахождение корней −2, −1 (повторяющийся корень) и −1/3 четверки 3 x ⁴ +13 x ³ +19 x ² +11 x +2 с использованием метода Лилла. Черные сегменты помечены своей длиной (коэффициенты в уравнении), в то время как каждая цветная линия с начальным наклоном m и той же конечной точкой соответствует действительному корню.

В математике , метод LILL в визуальном метод нахождения действительных корней из однофакторного полинома любой степени . ^[1] Он был разработан австрийским инженером Эдуардом Лиллем в 1867 году. ^[2] Более поздняя работа Лилля была посвящена проблеме сложных корней. ^[3]

Метод Лилля включает рисование пути из отрезков прямой, образующих прямые углы , с длинами, равными коэффициентам полинома. Затем корни полинома могут быть найдены как наклоны других прямоугольных путей, также соединяющих начало и конец, но с вершинами на линиях первого пути.

Описание метода

Нахождение корней −1/2, −1 / √ 2 и 1 / √ 2 кубики 4 x ³ +2 x ² −2 x −1, показывающих, как обрабатываются отрицательные коэффициенты и расширенные сегменты. Каждое число, показанное на цветной линии, является отрицательным значением его наклона и, следовательно, действительным корнем многочлена.

Чтобы использовать этот метод, рисуется диаграмма, начиная с начала координат. Линейный сегмент рисуется вправо на величину первого коэффициента (коэффициент члена с наибольшей степенью) (так, чтобы с отрицательным коэффициентом сегмент заканчивался слева от начала координат). От конца первого сегмента проводится другой сегмент вверх на величину второго коэффициента, затем влево на величину третьего и вниз на величину четвертого и т. Д. Последовательность направлений (не поворотов) всегда направо, вверх, влево, вниз, а затем повторяется. Таким образом, каждый поворот идет против часовой стрелки. Процесс продолжается для каждого коэффициента полинома, включая нули, с отрицательными коэффициентами, «идущими назад». Конечная точка, достигнутая в конце сегмента, соответствующего постоянному члену уравнения,это конечная остановка.

Затем линия запускается из начала координат под некоторым углом $θ$ , отражается от каждого сегмента линии под прямым углом (не обязательно «естественный» угол отражения) и преломляется под прямым углом через линию, проходящую через каждый сегмент (включая линия для нулевых коэффициентов), когда наклонный путь не попадает в сегмент линии на этой линии. ^[4] Вертикальные и горизонтальные линии отражаются от или преломляются через в следующей последовательности: строка , содержащую сегмент , соответствующий коэффициент затем т.д. Выбор $θ$ так, чтобы путь земля на конце, отрицательное тангенса $θ$ ${\ displaystyle x ^ {n-1},}$ ${\ displaystyle x ^ {n-2},}$ является корнем этого многочлена. Для каждого реального нуля многочлена будет один уникальный начальный угол и путь, который попадет в конечную точку. Например, квадратичный с двумя действительными корнями будет иметь ровно два угла, которые удовлетворяют указанным выше условиям.

Для комплексных корней также необходимо найти серию подобных треугольников, но с вершинами корневого пути, смещенными от полиномиального пути на расстояние, равное мнимой части корня. В этом случае корневой путь не будет прямоугольным. ^[5]^[3]

Объяснение

Действующая конструкция вычисляет многочлен в соответствии с методом Хорнера . Для полинома значения , , последовательно генерируются как расстояния между вершинами полиномиальных и корневыми путями. Для корня полинома конечное значение равно нулю, поэтому последняя вершина совпадает с концом пути полинома. ${\ displaystyle a_ {n} x ^ {n} + a_ {n-1} x ^ {n-1} + a_ {n-2} x ^ {n-2} + \ cdots}$ ${\ displaystyle a_ {n} x}$ ${\ Displaystyle (а_ {п} х + а_ {п-1}) х}$ $((a_{n}x+a_{n-1})x+a_{n-2})x,\ \dots$

Дополнительные свойства

Линия решения, дающая корень, аналогична конструкции Лилля для многочлена с удаленным корнем, потому что визуальная конструкция аналогична синтетическому делению многочлена на линейную (корневую) монику ( правило Руффини ).

Из симметрии диаграммы легко увидеть, что корни обращенного многочлена являются обратными исходным корням.

Конструкция также может быть выполнена с использованием поворотов по часовой стрелке вместо поворотов против часовой стрелки. Когда путь интерпретируется с использованием другого соглашения, он соответствует зеркально отраженному многочлену (каждый знак нечетного коэффициента изменен), а корни инвертируются.

Когда путь под прямым углом проходит в другом направлении, но с тем же соглашением о направлении, он соответствует перевернутому зеркально отраженному многочлену, а корни являются отрицательными обратными величинами исходных корней. ^[4]

Нахождение квадратных корней по теореме Фалеса

Нахождение корней из 3 x ² +5 x −2

Метод Лилла можно использовать с теоремой Фалеса, чтобы найти действительные корни квадратичного многочлена.

В этом примере с 3 x ² +5 x −2 сегменты линии многочлена сначала рисуются черным, как указано выше. Нарисуется круг с отрезком прямой линии, соединяющим начальную и конечную точки, образуя диаметр.

Согласно теореме Фалеса, треугольник, содержащий эти точки и любую другую точку на окружности, является прямоугольным треугольником . Пересечения этого круга со средним сегментом метода Лилла, при необходимости расширяемым, таким образом, определяют два наклонных пути в методе Лилла, окрашенные в синий и красный цвета.

Отрицательные значения градиентов их первых сегментов m дают действительные корни 1/3 и −2.

Поиск корней с помощью складывания бумаги

Найдите корни из 3x ³ + 2x ² −7x + 2

В 1936 году Маргарита Пьяццола Белох показала, как метод Лилла можно адаптировать для решения кубических уравнений с помощью складывания бумаги . ^[6] Если разрешены одновременные складки, то любое уравнение n- й степени с вещественным корнем может быть решено с использованием n –2 одновременных складок. ^[7]

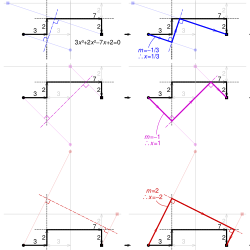
В этом примере с 3x ³ + 2x ² −7x + 2 отрезки линии многочлена сначала рисуются на листе бумаги (черным). Рисуются линии, проходящие через отражения начальной и конечной точек во втором и третьем сегментах соответственно (слабый кружок и квадрат) и параллельные им (серые линии).

Для каждого корня бумага складывается до тех пор, пока начальная точка (черный кружок) и конечная точка (черный квадрат) не будут отражены на этих линиях. Ось отражения (штрих-пунктирная линия) определяет наклонный путь, соответствующий корню (синий, фиолетовый и красный). Отрицательные значения градиентов их первых сегментов m дают действительные корни 1/3, 1 и −2.

Смотрите также

Круг Карлайла , основанный на слегка модифицированной версии метода Лилла для нормированной квадратичной системы.

использованная литература

^ Дэн Калман (2009). Необычные математические экскурсии: полиномия и связанные области . AMS. стр. 13 -22. ISBN 978-0-88385-341-2.
^ ME Lill (1867). «Графическое решение численных уравнений де тус градусов à une seule inconnue, и описание устройства, изобретенного в данс, но» (PDF) . Nouvelles Annales de Mathématiques . 2. 6 : 359–362.
^ a b М. Э. Лилль (1868). «Графическое решение для алгебраических уравнений Qui ont des racines imaginaires» (PDF) . Nouvelles Annales de Mathématiques . 2. 7 : 363–367.
^ а б Брэдфорд, Филлипс Вернер. «Визуализация решений алгебраических уравнений n-й степени с использованием прямоугольных геометрических путей» . www.concentric.net. Архивировано из оригинала 2 мая 2010 года . Проверено 3 февраля 2012 года .
^ Табачников, Серж (2017-03-01). «Многочлены как многоугольники» (PDF) . Математический интеллигент . 39 (1): 41–43. DOI : 10.1007 / s00283-016-9681-у . ISSN 1866-7414 .
↑ Томас С. Халл (апрель 2011 г.). «Решение кубиков со складками: работа Белоха и Лилля» (PDF) . Американский математический ежемесячник : 307–315. DOI : 10,4169 / amer.math.monthly.118.04.307 .
^ Роджер С. Альперин; Роберт Дж. Лэнг (2009). «Аксиомы одно-, двух- и многоуровневого оригами» (PDF) . 4OSME . А.К. Петерс.

внешние ссылки

Викискладе есть медиафайлы, связанные с методом Лилла .

Анимация для метода Лилла
Видео для математиков: «Решение уравнений путем стрельбы по черепахам с помощью лазера»

[1] Дэн Калман (2009). Необычные математические экскурсии: полиномия и связанные области . AMS. стр. 13 -22. ISBN 978-0-88385-341-2.

[2] ME Lill (1867). «Графическое решение численных уравнений де тус градусов à une seule inconnue, и описание устройства, изобретенного в данс, но» (PDF) . Nouvelles Annales de Mathématiques . 2. 6 : 359–362.

[:1-3] М. Э. Лилль (1868). «Графическое решение для алгебраических уравнений Qui ont des racines imaginaires» (PDF) . Nouvelles Annales de Mathématiques . 2. 7 : 363–367.

[:0-4] а б Брэдфорд, Филлипс Вернер. «Визуализация решений алгебраических уравнений n-й степени с использованием прямоугольных геометрических путей» . www.concentric.net. Архивировано из оригинала 2 мая 2010 года . Проверено 3 февраля 2012 года .

[5] Табачников, Серж (2017-03-01). «Многочлены как многоугольники» (PDF) . Математический интеллигент . 39 (1): 41–43. DOI : 10.1007 / s00283-016-9681-у . ISSN 1866-7414 .

[6] Томас С. Халл (апрель 2011 г.). «Решение кубиков со складками: работа Белоха и Лилля» (PDF) . Американский математический ежемесячник : 307–315. DOI : 10,4169 / amer.math.monthly.118.04.307 .

[7] Роджер С. Альперин; Роберт Дж. Лэнг (2009). «Аксиомы одно-, двух- и многоуровневого оригами» (PDF) . 4OSME . А.К. Петерс.

[1]