Группа точек
В геометрии группа точек — это математическая группа геометрических симметрий ( изометрий ), которые сохраняют фиксированной хотя бы одну точку. Точечные группы могут существовать в евклидовом пространстве любой размерности, и каждая точечная группа размерности d является подгруппой ортогональной группы O( d ). Группы точек могут быть реализованы как наборы ортогональных матриц M , которые преобразуют точку x в точку y :
где начало координат является фиксированной точкой. Элементы точечной группы могут быть либо вращениями ( определитель M = 1 ), либо отражениями , либо неправильными вращениями (определитель M = −1). Такой набор матриц называется представлением точечной группы.
Дискретные точечные группы более чем в одном измерении входят в бесконечные семейства, но из кристаллографической теоремы ограничения и одной из теорем Бибербаха каждое число измерений имеет только конечное число точечных групп, симметричных над некоторой решеткой или сеткой с этим числом. Это кристаллографические точечные группы .
Точечные группы можно разделить на хиральные (или чисто вращательные) группы и ахиральные группы. [1] Киральные группы являются подгруппами специальной ортогональной группы SO( d ): они содержат только ортогональные преобразования, сохраняющие ориентацию, т. е. детерминанта +1. Ахиральные группы содержат также преобразования определителя −1. В ахиральной группе преобразования, сохраняющие ориентацию, образуют (хиральную) подгруппу индекса 2.
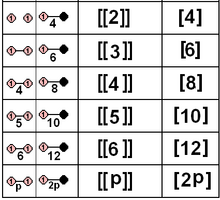
Конечные группы Кокстера или группы отражения — это те группы точек, которые генерируются исключительно набором отражающих зеркал, проходящих через одну и ту же точку. Группа Кокстера ранга n имеет n зеркал и представлена диаграммой Кокстера-Дынкина . Обозначение Кокстера предлагает обозначение в квадратных скобках, эквивалентное диаграмме Кокстера, с символами разметки для вращательных и других групп точек субсимметрии. Группы отражений обязательно ахиральны (за исключением тривиальной группы, содержащей только единичный элемент).
Применение кристаллографической теоремы об ограничении ограничивает n значениями 1, 2, 3, 4 и 6 для обоих семейств, что дает 10 групп.