Бернулли суд

Графики вероятности Р от не наблюдения независимых событий , каждый из вероятностей р после п испытаний Бернулли против нп для различного р . Показаны три примера:
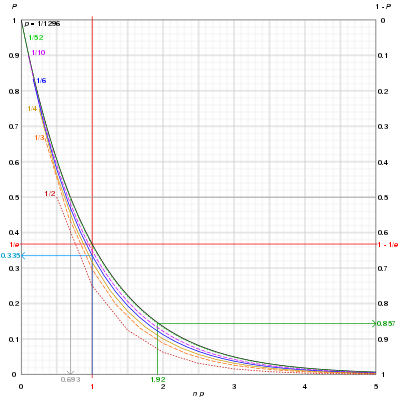
Синяя кривая : бросок 6-гранной кости 6 раз дает 33,5% шанс, что 6 (или любое другое заданное число) никогда не выпадет; можно заметить, что по мере увеличения n вероятность того, что случайное событие 1 / n никогда не появится после n попыток, быстро сходится к 0 .
Серая кривая : чтобы получить 50-50 шансов бросить Яхтзи(5 кубических кубиков показывают одно и то же число) требует 0,69 × 1296 ~ 898 бросков.
Зеленая кривая : Вытягивание карты из колоды игральных карт без джокеров 100 (1,92 × 52) раз с заменой дает 85,7% шанс вытянуть туз пик хотя бы один раз.

В теории вероятности и статистики , испытание Бернулли (или биномиальное испытание ) является случайным экспериментом ровно два возможных исходов , «успех» и «провал», в котором вероятность успеха является то же самое каждый раз , когда проводится эксперимент. ^[1] Он назван в честь Якоба Бернулли , швейцарского математика 17-го века, который проанализировал их в своей книге Ars Conjectandi (1713). ^[2]

Математическая формализация процесса Бернулли известна как процесс Бернулли . Эта статья предлагает элементарное введение в концепцию, тогда как статья о процессе Бернулли предлагает более продвинутую трактовку.

Поскольку у испытания Бернулли есть только два возможных исхода, его можно сформулировать как вопрос «да или нет». Например:

Является ли верхняя карта перетасованной колоды тузом?
Был ли новорожденный ребенок девочкой? (См. Соотношение полов человека .)

Следовательно, успех и неудача - это просто ярлыки для двух результатов, и их не следует толковать буквально. Термин «успех» в этом смысле означает результат, отвечающий определенным условиям, а не какое-либо моральное суждение. В более общем смысле, учитывая любое вероятностное пространство , для любого события (набора исходов) можно определить испытание Бернулли, соответствующее тому, произошло событие или нет (событие или дополнительное событие ). Примеры испытаний Бернулли включают:

Подбрасывание монеты. В этом контексте лицевая сторона («решка») условно означает успех, а обратная сторона («решка») - неудача. Справедливая монета имеет вероятность успеха 0,5 по определению. В этом случае есть ровно два возможных исхода.
Бросок кости , где шестерка - «успех», а все остальное - «неудача». В этом случае есть шесть возможных исходов, и событие - шесть; дополнительное событие «не шестерка» соответствует пяти другим возможным исходам.
При проведении опроса политического мнения выбор избирателя наугад, чтобы выяснить, проголосует ли этот избиратель «за» на предстоящем референдуме.

Определение [ править ]

Независимые повторные испытания эксперимента с двумя возможными исходами называются испытаниями Бернулли. Назовите один результат «успехом», а другой - «неудачей». Позвольте быть вероятностью успеха в испытании Бернулли, и быть вероятностью неудачи. Тогда вероятность успеха и вероятность неудачи в сумме равны единице, поскольку это взаимодополняющие события: «успех» и «неудача» взаимоисключают и исчерпывают . Таким образом, имеются следующие отношения: ${\ displaystyle p}$ ${\ displaystyle q}$

{\ Displaystyle p = 1-q, \ quad \ quad q = 1-p, \ quad \ quad p + q = 1.}

В качестве альтернативы, они могут быть сформулированы в терминах шансов : заданной вероятности р успеха и д неудачи, то шансы на это и шансы на которые Они также могут быть выражены в виде чисел, путем деления, что дает шансы на, и шансы против , ${\ displaystyle p: q}$ ${\ displaystyle q: p.}$ ${\ displaystyle o_ {f}}$ ${\ displaystyle o_ {a}:}$

{\ displaystyle {\ begin {align} o_ {f} & = p / q = p / (1-p) = (1-q) / q \\ o_ {a} & = q / p = (1-p ) / p = q / (1-q) \ end {выровнено}}}

Это мультипликативные инверсии , поэтому они умножаются на 1 со следующими соотношениями:

{\ displaystyle o_ {f} = 1 / o_ {a}, \ quad o_ {a} = 1 / o_ {f}, \ quad o_ {f} \ cdot o_ {a} = 1.}

В случае, если испытание Бернулли представляет собой событие из конечного числа равновероятных исходов , где S результатов являются успехом, а F результатов - неудачей, шансы на равны, а шансы против равны, Это дает следующие формулы для вероятности и шансы: ${\ displaystyle S: F}$ $F:S.$

{\begin{aligned}p&=S/(S+F)\\q&=F/(S+F)\\o_{f}&=S/F\\o_{a}&=F/S\end{aligned}}

Обратите внимание, что здесь шансы вычисляются путем деления количества исходов, а не вероятностей, но пропорция такая же, поскольку эти отношения различаются только умножением обоих членов на один и тот же постоянный коэффициент.

Случайные переменные, описывающие испытания Бернулли, часто кодируются с использованием соглашения, согласно которому 1 = «успех», 0 = «неудача».

Тесно связана с суда Бернулли является бином эксперимент, который состоит из фиксированного числа из статистически независимых испытаний Бернулли, каждый из которых с вероятностью успеха , и подсчитывает количество успехов. Случайная величина, соответствующая биному, обозначается и, как говорят, имеет биномиальное распределение . Вероятность именно успеха в эксперименте определяется выражением: $n$ $p$ $B(n,p)$ $k$ $B(n,p)$

P(k)={n \choose k}p^{k}q^{n-k}

где - биномиальный коэффициент . ${n \choose k}$

Испытания Бернулли также могут приводить к отрицательным биномиальным распределениям (которые подсчитывают количество успехов в серии повторных испытаний Бернулли до тех пор, пока не будет обнаружено определенное количество неудач), а также к различным другим распределениям.

Когда выполняется несколько испытаний Бернулли, каждое со своей вероятностью успеха, их иногда называют испытаниями Пуассона . ^[3]

Пример: подбрасывание монет [ править ]

Рассмотрим простой эксперимент, когда честная монета подбрасывается четыре раза. Найдите вероятность того, что ровно две подбрасывания завершатся орлом.

Решение [ править ]

Для этого эксперимента пусть орел будет успешным, а решка - неудачным. Поскольку предполагается, что монета является честной, вероятность успеха равна . Таким образом, вероятность отказа определяется выражением $p={\tfrac {1}{2}}$ $q$

q=1-p=1-{\tfrac {1}{2}}={\tfrac {1}{2}}

.

Используя приведенное выше уравнение, вероятность точно двух бросков из четырех, в результате которых выпадет орел, определяется как:

{\begin{aligned}P(2)&={4 \choose 2}p^{2}q^{4-2}\\&=6\times \left({\tfrac {1}{2}}\right)^{2}\times \left({\tfrac {1}{2}}\right)^{2}\\&={\dfrac {3}{8}}.\end{aligned}}

См. Также [ править ]

Схема Бернулли
Отбор проб Бернулли
Распределение Бернулли
Биномиальное распределение
Биномиальный коэффициент
Доверительный интервал биномиальной пропорции
Пуассоновская выборка
Дизайн выборки
Подбрасывание монет
Джейкоб Бернулли
Точный тест Фишера
Тест Босхлоо

Ссылки [ править ]

^ Папулиса, A. (1984). «Испытания Бернулли». Вероятность, случайные величины и случайные процессы (2-е изд.). Нью-Йорк: Макгроу-Хилл . С. 57–63.
^ Джеймс Виктор Успенский: Введение в математическую вероятность , McGraw-Hill, Нью-Йорк 1937, стр. 45
^ Раджив Мотвани и П. Рагхаван. Рандомизированные алгоритмы. Издательство Кембриджского университета, Нью-Йорк (Нью-Йорк), 1995, стр.67-68.

Внешние ссылки [ править ]

Викискладе есть средства массовой информации, связанные с судом над Бернулли .

"Испытания Бернулли" , Энциклопедия математики , EMS Press , 2001 [1994]
«Моделирование судебных процессов Бернулли» . math.uah.edu . Проверено 21 января 2014 .

[1] Папулиса, A. (1984). «Испытания Бернулли». Вероятность, случайные величины и случайные процессы (2-е изд.). Нью-Йорк: Макгроу-Хилл . С. 57–63.

[2] Джеймс Виктор Успенский: Введение в математическую вероятность , McGraw-Hill, Нью-Йорк 1937, стр. 45

[3] Раджив Мотвани и П. Рагхаван. Рандомизированные алгоритмы. Издательство Кембриджского университета, Нью-Йорк (Нью-Йорк), 1995, стр.67-68.

[1]