 | Эта статья требует дополнительных ссылок для проверки . ( январь 2017 г. ) ( Узнайте, как и когда удалить это сообщение-шаблон ) |
Кумулятивная функция распределения  | |||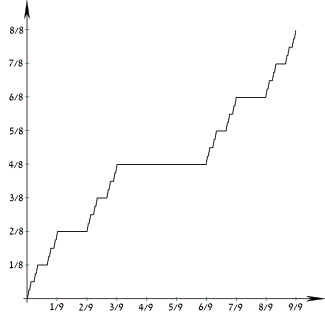
| Параметры | никто | ||
|---|---|---|---|
| Поддерживать | Кантор набор | ||
| PMF | никто | ||
| CDF | Функция Кантора | ||
| Иметь в виду | 1/2 | ||
| Медиана | где угодно в [1/3, 2/3] | ||
| Режим | н / д | ||
| Дисперсия | 1/8 | ||
| Асимметрия | 0 | ||
| Бывший. эксцесс | −8/5 | ||
| MGF | |||
| CF | |||
Распределение Кантора - это распределение вероятностей , совокупная функция распределения которого является функцией Кантора .
Это распределение не имеет ни функции плотности вероятности, ни функции массы вероятности , поскольку, хотя его кумулятивная функция распределения является непрерывной функцией , это распределение не является абсолютно непрерывным относительно меры Лебега и не имеет никаких точечных масс. Таким образом, это ни дискретное, ни абсолютно непрерывное распределение вероятностей, ни их смесь. Скорее это пример особого распределения .
Его кумулятивная функция распределения непрерывна повсюду, но почти везде горизонтальна, поэтому иногда ее называют лестницей Дьявола , хотя этот термин имеет более общее значение.
Характеристика [ править ]
Поддержка распределения Cantor является множество Кантора , само пересечение (счетно бесконечного числа множеств):
![{\ displaystyle {\ begin {align} C_ {0} = {} & [0,1] \\ [8pt] C_ {1} = {} & [0,1 / 3] \ чашка [2 / 3,1 ] \\ [8pt] C_ {2} = {} & [0,1 / 9] \ чашка [2 / 9,1 / 3] \ чашка [2 / 3,7 / 9] \ чашка [8/9, 1] \\ [8pt] C_ {3} = {} & [0,1 / 27] \ чашка [2 / 27,1 / 9] \ чашка [2 / 9,7 / 27] \ чашка [8/27 , 1/3] \ чашка \\ [4pt] {} & [2 / 3,19 / 27] \ чашка [20 / 27,7 / 9] \ чашка [8 / 9,25 / 27] \ чашка [26 / 27,1] \\ [8pt] C_ {4} = {} & [0,1 / 81] \ чашка [2 / 81,1 / 27] \ чашка [2 / 27,7 / 81] \ чашка [ 8 / 81,1 / 9] \ чашка [2 / 9,19 / 81] \ чашка [20 / 81,7 / 27] \ чашка \\ [4pt] и [8 / 27,25 / 81] \ чашка [ 26 / 81,1 / 3] \ чашка [2 / 3,55 / 81] \ чашка [56 / 81,19 / 27] \ чашка [20 / 27,61 / 81] \ чашка \\ [4pt] & [ 62 / 81,21 / 27] \ чашка [8 / 9,73 / 81] \ чашка [74 / 81,25 / 27] \ чашка [26 / 27,79 / 81] \ чашка [80 / 81,1] \\ [8pt] C_ {5} = {} & \ cdots \ end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066362d7de9b7a1d0bcf600d1dd5a2fcb9196ae4)
Распределение Кантора - это уникальное распределение вероятностей, для которого для любого C t ( t ∈ {0, 1, 2, 3, ...}) вероятность определенного интервала в C t, содержащего случайную величину с распределением Кантора, тождественно 2 - t на каждом из 2 t интервалов.
Моменты [ править ]
По симметрии легко увидеть, что для случайной величины X, имеющей такое распределение, ее математическое ожидание E ( X ) = 1/2 и что все нечетные центральные моменты X равны 0.
Закон общей дисперсии может быть использован , чтобы найти дисперсию Var ( X ), как показано ниже. Для указанного выше множества C 1 пусть Y = 0, если X ∈ [0,1 / 3], и 1, если X ∈ [2 / 3,1]. Потом:
Отсюда получаем:
Выражение в замкнутой форме для любого четного центрального момента можно найти, предварительно получив четные кумулянты [1]
где В 2 п есть 2 н е число Бернулли , а затем выразить моменты как функции кумулянтов .
Ссылки [ править ]
- ^ Моррисон, Кент (1998-07-23). «Случайные блуждания с убывающими шагами» (PDF) . Департамент математики Калифорнийского политехнического государственного университета . Проверено 16 февраля 2007 .
Дальнейшее чтение [ править ]
- Hewitt, E .; Стромберг, К. (1965). Реальный и абстрактный анализ . Берлин-Гейдельберг-Нью-Йорк: Springer-Verlag. В нем, как и в других стандартных текстах, есть функция Кантора и ее односторонние производные.
- Ху, Тянь-Ю; Лау, Ка Синг (2002). "Фурье-асимптотика мер канторова на бесконечности". Proc. AMS . 130 (9). С. 2711–2717. Это более современный текст, чем другие тексты в этом списке литературы.
- Книл, О. (2006). Теория вероятностей и случайные процессы . Индия: зарубежная пресса.
- Маттилла, П. (1995). Геометрия множеств в евклидовых пространствах . Сан-Франциско: Издательство Кембриджского университета. Здесь есть более продвинутый материал по фракталам.
