Эллипсоид Якоби

Художественная визуализация Хаумеа , карликовой планеты трехосного эллипсоида.

Якобите эллипсоид является трехосным (т.е. неравносторонним) эллипсоид при равновесии , которое возникает , когда самогравитирующее тело жидкости вращается однородной плотность с постоянной угловой скоростью. Он назван в честь немецкого математика Карла Густава Якоба Якоби . ^[1]

История [ править ]

До Якоби сфероид Маклорена , который был сформулирован в 1742 году, считался единственным типом эллипсоидов, который может находиться в равновесии. ^{[2] [3]} Лагранж в 1811 г. ^[4] рассмотрел возможность равновесия трехосного эллипсоида, но пришел к выводу, что две экваториальные оси эллипсоида должны быть равны, что привело к решению сфероида Маклорена . Но Якоби понял, что Лагранждемонстрация является достаточным, но не обязательным условием. Он заметил: «Можно было бы сделать серьезную ошибку, если бы кто-то предположил, что сфероиды вращения являются единственными допустимыми фигурами равновесия даже при ограничительном предположении о поверхностях второй степени» и далее добавляет, что «на самом деле простое рассмотрение показывает, что эллипсоиды с тремя неравные оси вполне могут быть фигурами равновесия; и что можно принять эллипс произвольной формы для экваториального сечения и определить третью ось (которая также является наименьшей из трех осей) и угловую скорость вращения так, чтобы эллипсоид фигура равновесия ". ^[5]

Формула Якоби [ править ]

Экваториальная ( a , b ) и полярная ( c ) полуглавные оси эллипсоида Якоби и сфероида Маклорена как функция нормированного углового момента при условии abc  = 1 (т.е. для постоянного объема 4π / 3).
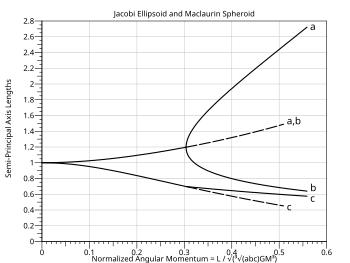
Пунктирные линии относятся к сфероиду Маклорена в диапазоне, в котором он обладает динамической, но не вековой стабильностью - он будет релаксировать в эллипсоид Якоби при условии, что он может рассеивать энергию за счет вязкой составляющей жидкости.

Для эллипсоида с экваториальными полуглавными осями и полярными полуглавными осями угловая скорость около определяется выражением${\ displaystyle a, \ b}$${\ displaystyle c}$${\ displaystyle \ Omega}$${\ displaystyle c}$

${\ displaystyle {\ frac {\ Omega ^ {2}} {\ pi G \ rho}} = 2abc \ int _ {0} ^ {\ infty} {\ frac {udu} {(a ^ {2} + u ) (b ^ {2} + u) \ Delta}} \, \ quad \ Delta ^ {2} = (a ^ {2} + u) (b ^ {2} + u) (c ^ {2} + u),}$

где - плотность, - гравитационная постоянная , при условии${\ displaystyle \ rho}$${\ displaystyle G}$

${\displaystyle a^{2}b^{2}\int _{0}^{\infty }{\frac {du}{(a^{2}+u)(b^{2}+u)\Delta }}=c^{2}\int _{0}^{\infty }{\frac {du}{(c^{2}+u)\Delta }}.}$

Для фиксированных значений и вышеупомянутое условие имеет решение для таких, что ${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\displaystyle {\frac {1}{c^{2}}}>{\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}.}$

Интегралы могут быть выражены через неполные эллиптические интегралы . ^[6] В терминах эллиптического интеграла симметричной формы Карлсона формула для угловой скорости принимает вид${\displaystyle R_{J}}$

${\displaystyle {\frac {\Omega ^{2}}{\pi G\rho }}={\frac {4abc}{3(a^{2}-b^{2})}}(a^{2}R_{J}(a^{2},b^{2},c^{2},a^{2})-b^{2}R_{J}(a^{2},b^{2},c^{2},b^{2}))}$

а условием относительного размера полуглавных осей является${\displaystyle a,\ b,\ c}$

${\displaystyle {\frac {2}{3}}{\frac {a^{2}b^{2}}{b^{2}-a^{2}}}(R_{J}(a^{2},b^{2},c^{2},a^{2})-R_{J}(a^{2},b^{2},c^{2},b^{2}))={\frac {2}{3}}c^{2}R_{J}(a^{2},b^{2},c^{2},c^{2}).}$

Угловой момент эллипсоида Якоби определяется выражением${\displaystyle L}$

${\displaystyle {\frac {L}{\sqrt {GM^{3}{\bar {a}}}}}={\frac {\sqrt {3}}{10}}{\frac {a^{2}+b^{2}}{{\bar {a}}^{2}}}{\sqrt {\frac {\Omega ^{2}}{\pi G\rho }}}\ ,\quad {\bar {a}}=(abc)^{1/3},}$

где - масса эллипсоида, а - средний радиус , радиус сферы того же объема, что и эллипсоид.${\displaystyle M}$${\displaystyle {\bar {a}}}$

Связь с эллипсоидом Дедекинда [ править ]

Эллипсоиды Якоби и Дедекинда являются фигурами равновесия для тела вращающейся однородной самогравитирующей жидкости. Однако в то время как эллипсоид Якоби вращается телесно, без внутреннего потока жидкости во вращающейся раме, эллипсоид Дедекинда сохраняет фиксированную ориентацию, а составляющая жидкость циркулирует внутри него. Это прямое следствие теоремы Дедекинда .

Для любого данного эллипсоида Якоби, существует дедекиндово эллипсоида с теми же полу-главных осей и той же массы , и с полем скоростей потока из ^[7]${\displaystyle a,\ b,\ c}$

${\displaystyle \mathbf {u} =\zeta {\frac {-a^{2}y\mathbf {\hat {x}} +b^{2}x\mathbf {\hat {y}} }{a^{2}+b^{2}}},}$

где декартовы координаты по осям, выровненным соответственно с осями эллипсоида. Вот это завихренность , которая однородна по сфероиду ( ). Угловая скорость эллипсоида Якоби и завихренность соответствующего эллипсоида Дедекинда связаны соотношением ^[7]${\displaystyle x,\ y,\ z}$${\displaystyle {\hat {x}},\ {\hat {y}},\ {\hat {z}}}$${\displaystyle a,\ b,\ c}$${\displaystyle \zeta }$${\displaystyle \nabla \times \mathbf {u} =\zeta \mathbf {\hat {z}} }$${\displaystyle \Omega }$

${\displaystyle \zeta =\left({\frac {a}{b}}+{\frac {b}{a}}\right)\Omega .}$

То есть каждая частица жидкости эллипсоида Дедекинда описывает подобный эллиптический контур в тот же период, в течение которого сфероид Якоби совершает один оборот.

В частном случае эллипсоиды Якоби и Дедекинда (и сфероид Маклорена) становятся одним и тем же; телесное вращение и круговой поток означают одно и то же. В этом случае , как всегда, для жестко вращающегося тела.${\displaystyle a=b}$${\displaystyle \zeta =2\Omega }$

В общем случае эллипсоиды Якоби и Дедекинда имеют одинаковую энергию ^[8], но угловой момент сфероида Якоби больше в ^{[8] раз.}

${\displaystyle {\frac {L_{\mathrm {Jac} }}{L_{\mathrm {Ded} }}}={\frac {1}{2}}\left({\frac {a}{b}}+{\frac {b}{a}}\right).}$

См. Также [ править ]

• Сфероид маклорена
• Эллипсоид Римана
• Эллипсоид Роша
• Эллипсоидальная задача Дирихле
• Сфероид
• Эллипсоид

Ссылки [ править ]