В геометрии , обобщенный многоугольник можно назвать Polygram , и назвал конкретно его числом сторон. Все полигоны являются полиграммами, но могут также включать в себя отдельные наборы ребер, называемые составным многоугольником . Например, обычная пентаграмма {5/2} имеет 5 сторон, а правильная гексаграмма {6/2} или 2 {3} имеет 6 сторон, разделенных на два треугольника.
Регулярно Polygram { р / д } может быть либо в наборе регулярных звездных многоугольников (для НОД ( р , д ) = 1, д > 1) или в наборе правильного многоугольника соединений (если НОД ( р , д )> 1). [1]
Этимология [ править ]
Имена полиграмм сочетают в себе числовой префикс , например пента- , с греческим суффиксом -грамма (в данном случае - слово пентаграмма ). Приставкой обычно является греческий кардинал , но существуют синонимы, использующие другие префиксы. В -gram суффикс происходит от γραμμῆς ( Grammos ) означает линию. [2]
Обобщенные правильные многоугольники [ править ]
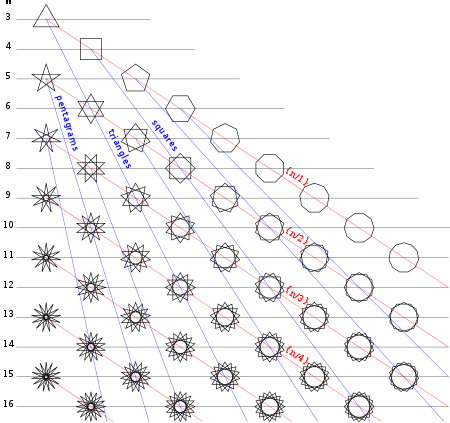
Регулярное Polygram, в качестве общего правильного многоугольника , обозначается его Шлефли символом { р / д }, где р и д являются взаимно простыми (они не разделяют ни одного фактора) и д ≥ 2. Для целых чисел р и д , то можно считать как построенные путем соединения каждой q- й точки из p точек, равномерно разнесенных по кругу. [3] [1]
 {5/2} |  {7/2} |  {7/3} |  {8/3} |  {9/2} |  {9/4} |  {10/3} ... |
Правильные составные многоугольники [ править ]
В других случаях, когда n и m имеют общий множитель, полиграмма интерпретируется как нижний многоугольник, { n / k , m / k }, с k = gcd ( n , m ), а повернутые копии объединяются как составной многоугольник. . Эти фигуры называются правильными составными многоугольниками .
| Треугольники ... | Квадраты ... | Пентагоны ... | Пентаграммы ... | ||||
|---|---|---|---|---|---|---|---|
{6/2} = 2 {3} | {9/3} = 3 {3} | {12/4} = 4 {3} | {8/2} = 2 {4} | {12/3} = 3 {4} | {10/2} = 2 {5} | {10/4} = 2 {5/2} | {15/6} = 3 {5/2} |
См. Также [ править ]
- Список правильных многогранников и соединений # Звезды
Ссылки [ править ]
- ^ a b Вайсштейн, Эрик В. "Полиграмм" . MathWorld .
- ^ γραμμή , Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон , о Персее
- ^ Кокстер, Гарольд Скотт Макдональд (1973). Правильные многогранники . Courier Dover Publications. п. 93 . ISBN 978-0-486-61480-9.
- Cromwell, P .; Многогранники , CUP, Hbk. 1997, ISBN 0-521-66432-2 . Pbk. (1999), ISBN 0-521-66405-5 . п. 175
- Грюнбаум, Б. и Г.К. Шепард; Плитки и узоры , Нью-Йорк: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
- Grünbaum, B .; Многогранники с полыми гранями, Материалы конференции NATO-ASI по многогранникам ... и т. Д. (Торонто, 1993) , изд. Т. Бистрички и др., Kluwer Academic (1994), стр. 43–70.
- Джон Х. Конвей , Хайди Берджел, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 404: Размерность 2 правильных звездно-многогранников)
- Роберт Лахлан, Элементарный трактат по современной чистой геометрии . Лондон: Macmillan, 1893, стр. 83 полиграммы. [1]
- Бранко Грюнбаум , Метаморфозы многоугольников , опубликованный в The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History , (1994)