Уравнение тепла
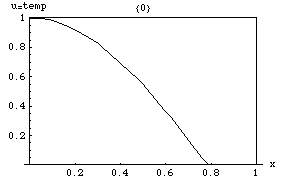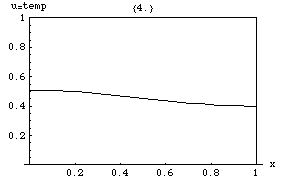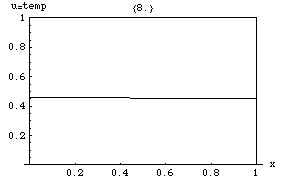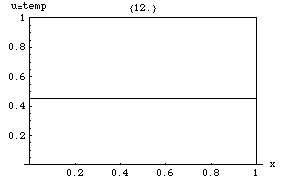
В математике и физике уравнение теплопроводности представляет собой некоторое дифференциальное уравнение в частных производных . Решения уравнения теплопроводности иногда называют калорическими функциями . Теория уравнения теплопроводности была впервые разработана Жозефом Фурье в 1822 году с целью моделирования того, как такая величина, как теплота , распространяется через заданную область.
В качестве прототипа параболического дифференциального уравнения в частных производных уравнение теплопроводности является одним из наиболее широко изучаемых тем в чистой математике , и его анализ считается фундаментальным для более широкой области дифференциальных уравнений в частных производных . Уравнение теплопроводности также можно рассматривать на римановых многообразиях , что приводит ко многим геометрическим приложениям. После работы Subbaramiah Minakshisundaram и Åke Pleijel уравнение теплопроводности тесно связано со спектральной геометрией . Основополагающий нелинейный вариант уравнения теплопроводности был введен в дифференциальную геометрию Джеймсом Иллсом иДжозефом Сэмпсоном в 1964 году, что вдохновило Ричарда Гамильтона на введение потока Риччи в 1982 году и завершилось доказательством гипотезы Пуанкаре Григорием Перельманом в 2003 году. Некоторые решения уравнения теплопроводности, известные как тепловые ядра , предоставляют тонкую информацию об области, в которой они определены, как показано на примере их применения к теореме Атьи-Зингера об индексе . [1]
Уравнение теплопроводности вместе с его вариантами также важно во многих областях науки и прикладной математики . В теории вероятностей уравнение теплопроводности связано с изучением случайных блужданий и броуновского движения через уравнение Фоккера-Планка . Уравнение Блэка-Шоулза в финансовой математике представляет собой небольшой вариант уравнения теплопроводности, а уравнение Шредингера в квантовой механике можно рассматривать как уравнение теплопроводности в мнимом времени . При анализе изображений уравнение теплопроводности иногда используется для устранения пикселизации иобозначить края . После введения Робертом Рихтмайером и Джоном фон Нейманом методов «искусственной вязкости» решения уравнений теплопроводности были полезны в математической формулировке гидродинамических ударов . Решениям уравнения теплопроводности также уделялось большое внимание в литературе по численному анализу , начиная с 1950-х годов с работ Джима Дугласа, Д. В. Писмана и Генри Рэчфорда-младшего.
В математике, если задано открытое подмножество U в Rn и подинтервал I в R , говорят, что функция u : U × I → R является решением уравнения теплопроводности, если
где ( x 1 , …, x n , t ) обозначает общую точку области. Обычно t называют «временем», а x 1 , …, x n — «пространственными переменными» даже в абстрактных контекстах, где эти фразы не имеют своего интуитивного значения. Набор пространственных переменных часто называют просто x . Для любого заданного значения t правая часть уравнения является лапласианом функции u (⋅, t ) : U → R. Таким образом, уравнение теплопроводности часто записывается более компактно как