| Аксиомы разделения в топологических пространствах | |
|---|---|
| Классификация Колмогорова | |
| Т 0 | (Колмогоров) |
| Т 1 | (Фреше) |
| Т 2 | (Хаусдорф) |
| Т 2 ½ | (Урысон) |
| полностью Т 2 | (полностью Хаусдорф) |
| Т 3 | (обычный Хаусдорф) |
| Т 3½ | (Тихонов) |
| Т 4 | (нормальный Хаусдорф) |
| Т 5 | (совершенно нормальный Хаусдорф) |
| Т 6 | (совершенно нормальный Хаусдорф) |
В топологии и смежных отраслей математики , тихоновских пространств и вполне регулярных пространств являются виды топологических пространств . Эти условия являются примерами аксиом разделения .
Тихоновские пространства названы в честь Андрея Николаевича Тихонова , русское имя которого (Тихонов) по-разному переводится как «Тихонов», «Тихонов», «Тихонов», «Тихонов» и т. Д., Который ввел их в 1930 году, чтобы избежать патологической ситуации Хаусдорфа. пространства , единственные непрерывные действительные функции которых являются постоянными отображениями. [1]
Определения [ править ]
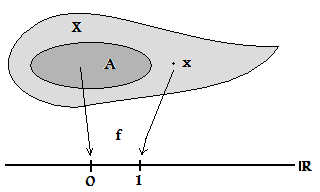
Топологическое пространство называется полностью регулярным именно в том случае, если точки можно отделить от замкнутых множеств с помощью (ограниченных) непрерывных вещественнозначных функций. С технической точки зрения это означает: для любого замкнутого множества и любой точки существует непрерывная функция с действительными значениями такая, что и (эквивалентно можно выбрать любые два значения вместо и и даже потребовать, чтобы они были ограниченной функцией.)
Топологическое пространство называется пространство тихоновский ( в качестве альтернативы: T 3½ пространство , или Т - П пространство , или полностью T 3 пространство ) , если это вполне регулярное хаусдорфово пространство .
Замечание. Вполне регулярные пространства и тихоновские пространства связаны понятием колмогоровской эквивалентности . Топологическое пространство тихоновское тогда и только тогда, когда оно полностью регулярно и T 0 . С другой стороны, пространство полностью регулярно тогда и только тогда, когда его фактор Колмогорова тихоновский.
Соглашения об именах [ править ]
В математической литературе применяются разные соглашения, когда речь идет о терминах «полностью регулярные» и «Т» -аксиомы. Определения в этом разделе даны в типичном современном использовании. Некоторые авторы, однако, меняют значения двух видов терминов или используют все термины как синонимы. В Википедии термины «полностью регулярный» и «тихоновский» используются свободно, а использование буквы «Т» обычно избегается. Поэтому в стандартной литературе рекомендуется проявлять осторожность, чтобы выяснить, какие определения использует автор. Для получения дополнительной информации по этому вопросу см. История аксиом разделения .
Примеры и контрпримеры [ править ]
Почти каждое топологическое пространство, изучаемое математическим анализом , тихоновское или, по крайней мере, полностью регулярное. Например, реальная прямая Тихонова по стандартной евклидовой топологии . Другие примеры включают:
- Каждое метрическое пространство тихоновское; каждое псевдометрическое пространство вполне регулярно.
- Каждое локально компактное регулярное пространство вполне регулярно, поэтому каждое локально компактное хаусдорфово пространство тихоновское.
- В частности, каждое топологическое многообразие тихоновское.
- Каждое полностью упорядоченное множество с порядковой топологией является Тихоновым.
- Каждая топологическая группа вполне регулярна.
- Обобщая как метрические пространства, так и топологические группы, каждое равномерное пространство полностью регулярно. Верно и обратное: всякое вполне регулярное пространство униформизимо.
- Каждый комплекс CW - Тихонов.
- Каждое нормальное регулярное пространство вполне регулярно, и каждое нормальное хаусдорфово пространство тихоново.
- Плоскость Немыцкая является примером пространства тихоновскома , который не является нормальным .
Свойства [ править ]
Сохранение [ править ]
Полная регулярность и свойство Тихонова хорошо работают по отношению к исходным топологиям . В частности, полная регулярность сохраняется при использовании произвольных начальных топологий, а свойство Тихонова сохраняется при выборе исходных топологий, разделяющих точки. Следует, что:
- Каждое подпространство полностью регулярного или тихоновского пространства обладает тем же свойством.
- Непустое пространство произведения является полностью регулярным (соответственно Тихоновым) тогда и только тогда, когда каждое фактор-пространство полностью регулярно (соответственно Тихоновское).
Как и все аксиомы разделения, полная регулярность не сохраняется при взятии окончательных топологий . В частности, частные вполне регулярных пространств не обязательно должны быть регулярными . Факторы тихоновских пространств не обязательно должны быть хаусдорфовыми . Есть замкнутые частные плоскости Мура, которые дают контрпримеры.
Непрерывные функции с действительным знаком [ править ]
Для любого топологического пространства X пусть C ( X ) обозначает семейство вещественнозначных непрерывных функций на X, а C b ( X ) - подмножество ограниченных вещественнозначных непрерывных функций.
Полностью регулярные пространства можно охарактеризовать тем, что их топология полностью определяется C ( X ) или C b ( X ). Особенно:
- Пространство X полностью регулярно тогда и только тогда, когда оно имеет начальную топологию, индуцированную C ( X ) или C b ( X ).
- Пространство X полностью регулярно тогда и только тогда, когда каждое замкнутое множество может быть записано как пересечение семейства нулевых множеств в X (т. Е. Нулевые множества образуют базис для замкнутых множеств X ).
- Пространство X вполне регулярно тогда и только тогда , когда конульмножества из X образуют базис для топологии X .
Для произвольного топологического пространства ( X , τ) существует универсальный способ связать вполне регулярное пространство с ( X , τ). Пусть ρ - начальная топология на X, индуцированная C τ ( X ), или, что то же самое, топология, порожденная базисом кон- нулевых множеств в ( X , τ). Тогда ρ будет тончайшей вполне регулярной топологией на X , более грубой, чем τ. Эта конструкция универсальна в том смысле, что любая непрерывная функция
в вполне регулярное пространство Y будет непрерывна на ( X , ρ). На языке теории категорий , в функтор , который посылает ( X , т) в ( X , р) сопряжен слева к включению функтора CreG → Top . Таким образом, категория вполне регулярных пространств CreG является отражательной подкатегорию из Top , в категории топологических пространств . Факторы Колмогорова показывают, что подкатегория тихоновских пространств также рефлексивна.
Можно показать , что С τ ( X ) = С ρ ( Х ) в приведенной выше конструкции так, чтобы кольца С ( Х ) и С Ь ( Х ) , как правило , изучаются только для вполне регулярного пространства X .
Категория вещественнокомпактных тихоновских пространств антиэквивалентна категории колец C ( X ) (где X вещественнокомпактно) вместе с гомоморфизмами колец как отображениями. Например, можно восстановить X из C ( X ), когда X (вещественное) компактно. Поэтому алгебраическая теория этих колец является предметом интенсивных исследований. Обширным обобщением этого класса колец, который все еще напоминает многие свойства тихоновских пространств, но также применим в реальной алгебраической геометрии , является класс вещественных замкнутых колец .
Вложения [ править ]
Тихоновские пространства - это в точности те пространства, которые могут быть вложены в компактные хаусдорфовы пространства . Точнее, для каждого тихоновского пространства X , существует бикомпакт K такое , что X является гомеоморфно подпространству К .
Фактически, всегда можно выбрать K как тихоновский куб (то есть, возможно, бесконечное произведение единичных интервалов ). Каждый Тихоновский куб компактен по Хаусдорфу в силу теоремы Тихонова . Поскольку каждое подпространство компактного хаусдорфового пространства тихоновское, у него есть:
- Топологическое пространство тихоновское тогда и только тогда, когда оно может быть вложено в тихоновский куб .
Компактификации [ править ]
Особый интерес представляют те вложения , где образ X является плотным в К ; они называются хаусдорфовы компактификациями из X . Принимая во внимание любое вложение тихоновского пространства X в компакте K замыкание образа X в K является компактификация X . В той же статье 1930 г., в которой Тихонов определил вполне регулярные пространства, он также доказал, что каждое тихоновское пространство имеет компактификацию Хаусдорфа. [2]
Среди этих компактификаций Хаусдорфа, существует единственный «самый общий» один, то стоун-чеховское β X . Он характеризуется универсальным свойством , что, учитывая непрерывное отображение F из X в любом другом бикомпакт Y , существует уникальный непрерывное отображение г от & beta ; X к Y , которая проходит п в том смысле , что F является композицией из г и j .
Единые структуры [ править ]
Полная регулярность - это как раз то условие, необходимое для существования однородных структур на топологическом пространстве. Другими словами, каждое равномерное пространство имеет совершенно правильную топологию и каждое вполне регулярное пространство X является униформизируемо . Топологическое пространство допускает разделенную равномерную структуру тогда и только тогда, когда оно тихоновское.
Учитывая вполне регулярное пространство X существует, как правило , больше , чем одна равномерности на X , который совместит с топологией X . Тем не менее, всегда будет лучшим совместимым единообразие, называется равномерность тонкой на X . Если Х является Тихоновское, то равномерная структура может быть выбрана таким образом , что β Х становится пополнение единого пространства X .
Цитаты [ править ]
- ^ Narici & Бекенштейн 2011 , стр. 240.
- ^ Narici & Бекенштейн 2011 , стр. 225-273.
Библиография [ править ]
- Гиллман, Леонард ; Джерисон, Мейер (1960). Кольца непрерывных функций . Тексты для выпускников по математике, № 43 (переиздание Дувра). Нью-Йорк: Springer-Verlag. п. xiii. ISBN 978-048681688-3.
- Наричи, Лоуренс ; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Уиллард, Стивен (1970). Общая топология (переиздание Дувра). Ридинг, Массачусетс: издательство Addison-Wesley Publishing Company. ISBN 0-486-43479-6.