Алгебраическая кривая

Кубика чирнгауза является алгебраической кривой степени три.

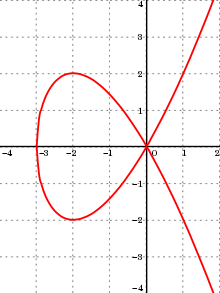
В математике , аффинное алгебраическое плоская кривая представляет собой множество нулей из многочлена от двух переменных. Проективное алгебраическое плоская кривая представляет множество нулей в проективной плоскости в виде однородного многочлена от трех переменных. Аффинная алгебраическая плоская кривая может быть завершена в проективной алгебраической плоской кривой путем усреднения ее определяющего полинома. И наоборот, проективная алгебраическая плоская кривая однородного уравнения h ( x , y , t ) = 0 может быть ограничена аффинной алгебраической плоской кривой уравнения h( х , у , 1) = 0 . Каждая из этих двух операций противоположна другой; поэтому фраза « алгебраическая плоская кривая» часто используется без явного указания, является ли рассматриваемый случай аффинным или проективным.

Более общо, алгебраическая кривая представляет собой алгебраическое многообразие из размерности один. Эквивалентно, алгебраическая кривая - это алгебраическое многообразие, которое бирационально эквивалентно алгебраической плоской кривой. Если кривая содержится в аффинном или проективном пространстве , для такой бирациональной эквивалентности можно взять проекцию .

Эти бирациональные эквивалентности сводят большую часть изучения алгебраических кривых к изучению алгебраических плоских кривых. Однако некоторые свойства не соблюдаются при бирациональной эквивалентности и должны изучаться на неплоских кривых. В частности, это касается степени и гладкости . Например, существуют гладкие кривые рода 0 и степени больше двух, но любая плоская проекция таких кривых имеет особые точки (см. Формулу род – степень ).

Неплоская кривая часто называется пространственной кривой или косой кривой .

В евклидовой геометрии [ править ]

Алгебраическая кривая на евклидовой плоскости - это набор точек, координаты которых являются решениями двумерного полиномиального уравнения p ( x , y ) = 0. Это уравнение часто называют неявным уравнением кривой, в отличие от кривых, которые являются графиком функции, явно определяющей y как функцию от x .

Для кривой, заданной таким неявным уравнением, первая задача состоит в том, чтобы определить форму кривой и нарисовать ее. Эти проблемы не так легко решить, как в случае графика функции, для которого y можно легко вычислить для различных значений x . Тот факт, что определяющее уравнение является полиномом, означает, что кривая обладает некоторыми структурными свойствами, которые могут помочь в решении этих проблем.

Каждую алгебраическую кривую можно однозначно разложить на конечное число гладких монотонных дуг (также называемых ветвями ), иногда соединенных некоторыми точками, иногда называемыми «замечательными точками», и, возможно, конечным числом изолированных точек, называемых узлами . Гладкая монотонная дуга является графиком гладкой функции , которая определяется и монотонная на открытом интервал из й Оу. В каждом направлении дуга либо неограничена (обычно называемая бесконечной дугой ), либо имеет конечную точку, которая является либо особой точкой (это будет определено ниже), либо точкой с касательной, параллельной одной из осей координат.

Например, для кубики Чирнхаузена есть две бесконечные дуги, имеющие начало (0,0) в качестве конечной точки. Эта точка - единственная особая точка кривой. Есть также две дуги, имеющие эту особую точку в качестве одной конечной точки и имеющие вторую конечную точку с горизонтальной касательной. Наконец, есть две другие дуги, каждая из которых имеет одну из этих точек с горизонтальной касательной в качестве первой конечной точки и уникальную точку с вертикальной касательной в качестве второй конечной точки. Напротив, синусоида , конечно, не алгебраическая кривая, имеющая бесконечное количество монотонных дуг.

Чтобы нарисовать алгебраическую кривую, важно знать замечательные точки и их касательные, бесконечные ветви и их асимптоты (если они есть), а также то, как дуги соединяют их. Также полезно рассматривать точки перегиба как замечательные точки. Когда вся эта информация нанесена на лист бумаги, форма кривой обычно видна довольно четко. Если нет, достаточно добавить несколько других точек и их касательные, чтобы получить хорошее описание кривой.

Методы вычисления замечательных точек и их касательных описаны ниже, после раздела Проективные кривые .

Плоские проективные кривые [ править ]

Часто желательно рассматривать кривые в проективном пространстве . Алгебраическая кривая на проективной плоскости или плоская проективная кривая - это множество точек на проективной плоскости , проективные координаты которых являются нулями однородного многочлена от трех переменных P ( x , y , z ).

Каждую аффинную алгебраическую кривую уравнения p ( x , y ) = 0 можно дополнить до проективной кривой уравнения, где${\ Displaystyle ^ {ч} п (х, у, г) = 0,}$

${\ Displaystyle ^ {ч} п (х, у, г) = г ^ {\ градус (р)} р ({\ tfrac {х} {z}}, {\ tfrac {y} {z}})}$

является результатом гомогенизации из р . Наоборот, если P ( x , y , z ) = 0 - однородное уравнение проективной кривой, то P ( x , y , 1) = 0 - уравнение аффинной кривой, состоящей из точек проективной кривой третья проективная координата которого не равна нулю. Эти две операции взаимны друг с другом, поскольку и, если p определяется , то , как только однородный многочлен P не делится на z .${\ Displaystyle ^ {ч} п (х, у, 1) = р (х, у)}$${\ Displaystyle р (х, у) = п (х, у, 1)}$${\ Displaystyle ^ {ч} п (х, у, г) = п (х, у, г),}$

Например, проективная кривая уравнения x ² + y ² - z ² является проективным завершением единичной окружности уравнения x ² + y ² - 1 = 0.

Это означает, что аффинная кривая и ее проективное пополнение являются одними и теми же кривыми, или, точнее, что аффинная кривая является частью проективной кривой, которая достаточно велика, чтобы хорошо определять «полную» кривую. Эта точка зрения обычно выражается, называя «бесконечно удаленными точками» аффинной кривой точки (в конечном числе) проективного пополнения, не принадлежащие аффинной части.

Проективные кривые часто исследуют сами по себе. Они также полезны для изучения аффинных кривых. Например, если p ( x , y ) - многочлен, определяющий аффинную кривую, помимо частных производных и , полезно рассматривать производную на бесконечности${\ displaystyle p '_ {x}}$${\ displaystyle p '_ {y}}$

${\ displaystyle p '_ {\ infty} (x, y) = {^ {h} p' _ {z} (x, y, 1)}.}.$

Например, уравнение касательной к аффинной кривой уравнения p ( x , y ) = 0 в точке ( a , b ) имеет вид

${\ displaystyle xp '_ {x} (a, b) + yp' _ {y} (a, b) + p '_ {\ infty} (a, b) = 0.}$

Замечательные точки плоской кривой [ править ]

В этом разделе мы рассмотрим плоскую алгебраическую кривые , определенный двумерный полином р ( х , у ) и ее проективное завершения, определяемые гомогенизации из р .${\ Displaystyle P (x, y, z) = {} ^ {h} p (x, y, z)}$

Пересечение с линией [ править ]

Часто бывает полезно знать точки пересечения кривой с данной линией. Пересечение с осями координат и асимптотами полезно для построения кривой. Пересечение линией, параллельной осям, позволяет найти хотя бы точку на каждой ветви кривой. Если доступен эффективный алгоритм поиска корней , это позволяет рисовать кривую, нанося точку пересечения со всеми линиями, параллельными оси y и проходящими через каждый пиксель на оси x .

Если полином, определяющий кривую, имеет степень d , любая прямая разрезает кривую не более чем на d точек. Теорема Безу утверждает, что это число равно d , если точки ищутся на проективной плоскости над алгебраически замкнутым полем (например, комплексные числа ) и считаются с их кратностью . Следующий метод вычислений еще раз доказывает эту теорему в этом простом случае.

Чтобы вычислить пересечение кривой, определяемой полиномом p, с линией уравнения ax + by + c = 0, решается уравнение прямой для x (или для y, если a = 0). Подставляя результат в p , получаем одномерное уравнение q ( y ) = 0 (или q ( x ) = 0, если уравнение прямой было решено в y), каждый из корней которой является одной координатой точки пересечения. Другая координата выводится из уравнения линии. Кратность точки пересечения - это кратность соответствующего корня. Точка пересечения находится на бесконечности, если степень q меньше степени p ; кратность такой бесконечно удаленной точки пересечения равна разности степеней p и q .

Касательная в точке [ править ]

Касательная в точке ( a , b ) кривой - это линия уравнения , как и для любой дифференцируемой кривой, определенной неявным уравнением. В случае полиномов другая формула касательной имеет более простой постоянный член и более симметрична:${\ displaystyle (xa) p '_ {x} (a, b) + (yb) p' _ {y} (a, b) = 0}$

${\displaystyle xp'_{x}(a,b)+yp'_{y}(a,b)+p'_{\infty }(a,b)=0,}$

где - производная на бесконечности. Эквивалентность двух уравнений результатов теоремы Эйлера однородной функции применительно к Р .${\displaystyle p'_{\infty }(x,y)=P'_{z}(x,y,1)}$

Если касательная не определена и точка является особой точкой .${\displaystyle p'_{x}(a,b)=p'_{y}(a,b)=0,}$

Это немедленно распространяется на проективный случай: уравнение касательной к в точке проективных координат ( a : b : c ) проективной кривой уравнения P ( x , y , z ) = 0 равно

${\displaystyle xP'_{x}(a,b,c)+yP'_{y}(a,b,c)+zP'_{z}(a,b,c)=0,}$

а особые точки кривых - это такие точки, что

${\displaystyle P'_{x}(a,b,c)=P'_{y}(a,b,c)=P'_{z}(a,b,c)=0.}$

(Условие P ( a , b , c ) = 0 вытекает из этих условий по теореме Эйлера об однородных функциях.)

Асимптоты [ править ]

Каждая бесконечная ветвь алгебраической кривой соответствует бесконечно удаленной точке кривой, то есть точке проективного пополнения кривой, не принадлежащей ее аффинной части. Соответствующая асимптота является касательной к кривой в этой точке. Может применяться общая формула касательной к проективной кривой, но в этом случае стоит сделать ее явной.

Пусть - разложение многочлена, определяющего кривую, на ее однородные части, где p _i - сумма мономов от p степени i . Следует, что${\displaystyle p=p_{d}+\cdots +p_{0}}$

${\displaystyle P={^{h}p}=p_{d}+zp_{d-1}+\cdots +z^{d}p_{0}}$

и

${\displaystyle P'_{z}(a,b,0)=p_{d-1}(a,b).}$

Бесконечная точка кривой - это нуль p вида ( a , b , 0). Эквивалентно ( a , b ) - это ноль p _d . Из фундаментальной теоремы алгебры следует, что над алгебраически замкнутым полем (обычно полем комплексных чисел) p _d разлагается на произведение линейных множителей. Каждый фактор определяет бесконечно удаленную точку на кривой: если bx  -  ay является таким фактором, то он определяет бесконечно удаленную точку ( a , b , 0). По реалам, p _dделится на линейные и квадратичные множители. В неприводимые квадратичные факторы определяют невещественные точки на бесконечности, а реальные точки задаются линейные множители. Если ( a , b , 0) - бесконечно удаленная точка кривой, говорят, что ( a , b ) - асимптотическое направление . Положив q = p _d, уравнение соответствующей асимптоты имеет вид

${\displaystyle xq'_{x}(a,b)+yq'_{y}(a,b)+p_{d-1}(a,b)=0.}$

Если и асимптота - это линия на бесконечности, а в реальном случае кривая имеет ветвь, которая выглядит как парабола . В этом случае говорят, что кривая имеет параболическую ветвь . Если${\displaystyle q'_{x}(a,b)=q'_{y}(a,b)=0}$${\displaystyle p_{d-1}(a,b)\neq 0,}$

${\displaystyle q'_{x}(a,b)=q'_{y}(a,b)=p_{d-1}(a,b)=0,}$

кривая имеет особую точку на бесконечности и может иметь несколько асимптот. Их можно вычислить методом вычисления касательного конуса особой точки.

Особые точки [ править ]

В особых точках кривой степени д , определяемый многочлен р ( х , у ) степени г являются решениями системы уравнений:

${\displaystyle p'_{x}(x,y)=p'_{y}(x,y)=p(x,y)=0.}$

В нулевой характеристике эта система эквивалентна

${\displaystyle p'_{x}(x,y)=p'_{y}(x,y)=p'_{\infty }(x,y)=0,}$

где, в обозначениях предыдущего раздела, системы эквивалентны в силу теоремы Эйлера об однородных функциях . Последняя система имеет то преимущество, что у нее третий многочлен степени d -1 вместо d .${\displaystyle p'_{\infty }(x,y)=P'_{z}(x,y,1).}$

Аналогично, для проективной кривой, задаваемой однородным многочленом P ( x , y , z ) степени d , особые точки имеют решения системы

${\displaystyle P'_{x}(x,y,z)=P'_{y}(x,y,z)=P'_{z}(x,y,z)=0}$

как однородные координаты . (При положительной характеристике уравнение необходимо добавить в систему.)${\displaystyle P(x,y,z)}$

Это означает, что число особых точек конечно, пока p ( x , y ) или P ( x , y , z ) не содержит квадратов . Таким образом, из теоремы Безу следует, что количество особых точек не превосходит ( d −1) ² , но эта оценка не является точной, поскольку система уравнений переопределена . Если приводимые полиномы разрешены, точная граница равна d ( d −1) / 2, это значение достигается, когда полиномиальные множители в линейных множителях, то есть если кривая является объединением dлиний. Для неприводимых кривых и многочленов количество особых точек не превосходит ( d −1) ( d −2) / 2 из-за формулы, выражающей род через особенности (см. Ниже). Максимума достигают кривые рода нуль, все особенности которых имеют кратность два и различные касательные (см. Ниже).

Уравнение касательных в особой точке задается ненулевой однородной частью младшей степени в ряду Тейлора многочлена в особой точке. Когда вы меняете координаты, чтобы поместить особую точку в начало координат, уравнение касательных в особой точке, таким образом, является ненулевой однородной частью низшей степени полинома, а кратность особой точки является степенью этого однородного часть.

Аналитическая структура [ править ]

Изучение аналитической структуры алгебраической кривой в окрестности особой точки дает точную информацию о топологии особенностей. Фактически, вблизи особой точки реальная алгебраическая кривая представляет собой объединение конечного числа ветвей, которые пересекаются только в особой точке и выглядят либо как куспид, либо как гладкая кривая.

Вблизи регулярной точки одна из координат кривой может быть выражена как аналитическая функция другой координаты. Это следствие теоремы об аналитической неявной функции , из которого следует, что кривая гладкая вблизи точки. Вблизи особой точки ситуация более сложная и включает ряды Пюизо , которые дают аналитические параметрические уравнения ветвей.

Для описания особенности стоит перевести кривую на наличие сингулярности в начале координат. Он состоит в замене переменной вида где - координаты особой точки. В дальнейшем предполагается, что рассматриваемая особая точка всегда находится в начале координат.${\displaystyle X=x-a,Y=y-b,}$${\displaystyle a,b}$

Уравнение алгебраической кривой - это где f - многочлен от x и y . Этот многочлен можно рассматривать как многочлен от y с коэффициентами в алгебраически замкнутом поле ряда Пюизо по x . Таким образом, f можно разложить на множители вида где P - ряд Пюизо. Все эти множители различны, если f является неприводимым многочленом , потому что это означает, что f не содержит квадратов , а это свойство не зависит от поля коэффициентов.${\displaystyle f(x,y)=0,}$${\displaystyle y-P(x),}$

Встречающиеся здесь серии Пюизе имеют вид

${\displaystyle P(x)=\sum _{n=n_{0}}^{\infty }a_{n}x^{n/d},}$

где d - положительное целое число, и это целое число, которое также можно считать положительным, поскольку мы рассматриваем только те ветви кривой, которые проходят через начало координат. Без ограничения общности можно считать , что d является взаимно просты с наибольшим общим делителем п такое , что ( в противном случае можно было бы выбрать меньший общий знаменатель для показателей).${\displaystyle n_{0}}$${\displaystyle a_{n}\neq 0}$

Позвольте быть примитивным корнем степени d из единицы . Если указанный выше ряд Пюизо встречается при факторизации , то ряд d${\displaystyle \omega _{d}}$${\displaystyle f(x,y)=0}$

${\displaystyle P_{i}(x)=\sum _{n=n_{0}}^{\infty }a_{n}\omega _{d}^{i}x^{n/d}}$

возникают также при факторизации (следствие теории Галуа ). Эти d- ряды называются сопряженными и рассматриваются как одна ветвь кривой индекса ветвления d .

В случае действительной кривой, то есть кривой, определяемой полиномом с действительными коэффициентами, могут иметь место три случая. Если ни у одного нет действительных коэффициентов, значит, у одного есть ненастоящая ветвь. Если некоторые из них имеют реальные коэффициенты, их можно выбрать как . Если d нечетно, то каждое реальное значение x дает реальное значение , и у одного есть реальная ветвь, которая выглядит регулярной, хотя она сингулярна, если d > 1 . Если d четно, то и имеют действительные значения, но только для x ≥ 0 . В этом случае реальная ветвь выглядит как куспид (или как куспид, в зависимости от определения используемого куспида).${\displaystyle P_{i}(x)}$${\displaystyle P_{i}(x)}$${\displaystyle P_{0}(x)}$${\displaystyle P_{0}(x)}$${\displaystyle P_{0}(x)}$${\displaystyle P_{d/2}(x)}$

Например, у обычного куспида всего одна ветвь. Если это определяется уравнением, то факторизация - это индекс ветвления, равный 2, и два фактора действительны и определяют каждую половину ветви. Если куспид поворачивается, уравнение становится равным, а факторизация - с (коэффициент не был упрощен до j, чтобы показать, насколько специализировано приведенное выше определение ). Здесь индекс ветвления равен 3, и действителен только один фактор; это показывает, что в первом случае эти два фактора должны рассматриваться как определяющие одну и ту же ветвь.${\displaystyle y^{2}-x^{3}=0,}$${\displaystyle (y-x^{3/2})(y+x^{3/2});}$${\displaystyle y^{3}-x^{2}=0,}$${\displaystyle (y-x^{2/3})(y-j^{2}x^{2/3})(y-(j^{2})^{2}x^{2/3}),}$${\displaystyle j=(1+{\sqrt {-3}})/2}$${\displaystyle (j^{2})^{2}}$${\displaystyle P_{i}(x)}$

Неплоские алгебраические кривые [ править ]

Алгебраическая кривая представляет собой алгебраическое многообразие из размерности один. Это означает, что аффинная кривая в аффинном пространстве размерности n определяется, по крайней мере, n - 1 многочленом от n переменных. Для того, чтобы определить кривую, эти многочлены должны генерировать простой идеал в размерности Крулля 1. Это условие не легко проверить на практике. Следовательно, может быть предпочтительным следующий способ представления неплоских кривых.

Пусть есть n многочленов от двух переменных x ₁ и x _2, таких что f неприводима. Точки аффинного пространства размерности n , координаты которых удовлетворяют уравнениям и неравенствам${\displaystyle f,g_{0},g_{3},\ldots ,g_{n}}$

${\displaystyle {\begin{aligned}&f(x_{1},x_{2})=0\\&g_{0}(x_{1},x_{2})\neq 0\\x_{3}&={\frac {g_{3}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\\&{}\ \vdots \\x_{n}&={\frac {g_{n}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\end{aligned}}}$

- все точки алгебраической кривой, из которых удалено конечное число точек. Эта кривая определяется системой образующих идеала многочленов h таких, что существует такое целое число k , которое принадлежит идеалу, порожденному . Это представление является бирациональной эквивалентностью кривой и плоской кривой, определяемой f . Таким образом можно представить любую алгебраическую кривую. Однако может потребоваться линейная замена переменных, чтобы почти всегда вводить проекцию на две первые переменные. Когда необходима замена переменных, почти каждое изменение удобно, если оно определяется над бесконечным полем.${\displaystyle g_{0}^{k}h}$${\displaystyle f,x_{3}g_{0}-g_{3},\ldots ,x_{n}g_{0}-g_{n}}$

Это представление позволяет нам легко вывести любое свойство неплоской алгебраической кривой, включая ее графическое представление, из соответствующего свойства ее плоской проекции.

Для кривой, определяемой ее неявными уравнениями, приведенное выше представление кривой может быть легко выведено из базиса Грёбнера для упорядочения блоков , так что блок меньших переменных равен ( x ₁ , x ₂ ). Многочлен f - это единственный многочлен в базе, который зависит только от x ₁ и x ₂ . Дроби g _i / g ₀ получаются выбором для i = 3, ..., n многочлена в базисе, линейного по x _i и зависящего только от x₁ , x ₂ и x _i . Если этот выбор невозможен, это означает, что либо уравнения определяют алгебраическое множество , которое не является разновидностью, либо многообразие не имеет размерности один, либо необходимо изменить координаты. Последний случай имеет место, когда f существует и единственно, и для i = 3, ..., n существуют многочлены, старший моном которых зависит только от x ₁ , x ₂ и x _i .

Поля алгебраических функций [ править ]

Изучение алгебраических кривых можно свести к изучению неприводимых алгебраических кривых: тех кривых, которые нельзя записать как объединение двух меньших кривых. Вплоть до бирациональной эквивалентности, неприводимые кривые над полем F являются категорически эквивалентны для полей алгебраических функций одной переменной над F . Такое поле алгебраических функций является расширение поля К из F , который содержит элемент х , который является трансцендентным над F , и такой , что К является конечным алгебраическим расширением F (х ), которая является полем рациональных функций в неопределенном х над  F .

Например, рассмотрим поле C комплексных чисел, над которыми мы можем определить поле С ( х ) рациональных функций в  С . Если y ²  =  x ³  -  x  - 1, то поле C ( x ,  y ) является полем эллиптических функций . Элемент x не определен однозначно; поле также можно рассматривать, например, как расширение C ( y ). Алгебраическая кривая, соответствующая полю функции, - это просто набор точек ( x ,  y ) вC ² такая, что y ²  =  x ³  -  x  - 1.

Если поле F не является алгебраически замкнутым, точка зрения на функциональные поля немного шире, чем рассмотрение геометрического места точек, поскольку мы включаем, например, «кривые» без точек на них. Например, если базовое поле F является полем R действительных чисел, то x ²  +  y ²  = −1 определяет поле алгебраического расширения R ( x ), но соответствующая кривая, рассматриваемая как подмножество R ^2, не имеет точек . Уравнение x ²  +  y ²  = −1 действительно определяет неприводимую алгебраическую кривую над Rв схеме смысле (в интеграле , разделенная одномерные схемы из конечного типа над R ). В этом смысле взаимно однозначное соответствие между неприводимыми алгебраическими кривыми над F (с точностью до бирациональной эквивалентности) и полями алгебраических функций от одной переменной над F, вообще говоря, выполняется.

Две кривые могут быть бирационально эквивалентными (т. Е. Иметь изоморфные функциональные поля), не будучи изоморфными как кривые. Ситуация становится проще, когда мы имеем дело с неособыми кривыми, т. Е. Такими, которые не имеют особенностей. Две неособые проективные кривые над полем изоморфны тогда и только тогда, когда их функциональные поля изоморфны.

Теорема Цена касается функционального поля алгебраической кривой над алгебраически замкнутым полем.

Сложные кривые и реальные поверхности [ править ]

Комплексная проективная алгебраическая кривая находится в n -мерном комплексном проективном пространстве CP ⁿ . Оно имеет комплексную размерность n , но топологическую размерность, как реальное многообразие , 2 n , является компактным , связным и ориентируемым . Алгебраическая кривая над C также имеет топологическую размерность два; другими словами, это поверхность .

В топологическом роде этой поверхности, то есть число ручек или пончик отверстий, равно к геометрическим роду алгебраических кривому , которые могут быть вычислены с помощью алгебраических средств. Короче говоря, если рассматривать плоскую проекцию неособой кривой, имеющей степень d и только обычные особенности (особенности кратности два с различными касательными), то род равен ( d  - 1) ( d  - 2) / 2 -  k , где k - количество этих особенностей.

Компактные римановы поверхности [ править ]

Риманова поверхность является связным комплексным аналитическим многообразием одного комплексного измерения, что делает его связным вещественное многообразием двух измерений. Оно компактно, если компактно как топологическое пространство.

Существует тройная эквивалентность категорий между категорией гладких неприводимых проективных алгебраических кривых над C (с непостоянными регулярными отображениями в качестве морфизмов), категорией компактных римановых поверхностей (с непостоянными голоморфными отображениями в качестве морфизмов) и противоположностью категории категория полей алгебраических функций от одной переменной над C (с гомоморфизмами полей, фиксирующими Cкак морфизмы). Это означает, что, изучая эти три предмета, мы в некотором смысле изучаем одно и то же. Это позволяет использовать сложные аналитические методы в алгебраической геометрии, а алгебро-геометрические методы в комплексном анализе и теоретико-полевые методы - в обоих. Это характерно для гораздо более широкого класса задач алгебраической геометрии.

См. Также алгебраическую геометрию и аналитическую геометрию для более общей теории.

Особенности [ править ]

Используя внутреннюю концепцию касательного пространства , точки P на алгебраической кривой C классифицируются как гладкие (синоним: неособые ) или особые . Учитывая n −1 однородных многочленов от n +1 переменных, мы можем найти матрицу Якоби как ( n −1) × ( n +1) матрицу частных производных. Если ранг этой матрицы равен n - 1, то многочлены определяют алгебраическую кривую (в противном случае они определяют алгебраическое многообразие более высокой размерности). Если ранг остается n−1, когда матрица Якоби вычисляется в точке P на кривой, то эта точка является гладкой или регулярной точкой; в противном случае это особая точка . В частности, если кривая является плоской проективной алгебраической кривой, определенной одним однородным полиномиальным уравнением f ( x , y , z ) = 0, то особые точки - это в точности точки P, в которых ранг 1 × ( n + 1) матрица нулевая, то есть где

${\displaystyle {\frac {\partial f}{\partial x}}(P)={\frac {\partial f}{\partial y}}(P)={\frac {\partial f}{\partial z}}(P)=0.}$

Поскольку f - многочлен, это определение является чисто алгебраическим и не делает никаких предположений о природе поля F , которое, в частности, не обязательно должно быть действительными или комплексными числами. Конечно, следует помнить, что (0,0,0) не является точкой кривой и, следовательно, не является особой точкой.

Аналогично, для аффинной алгебраической кривой, определенной одним полиномиальным уравнением f ( x , y ) = 0, то особые точки - это в точности точки P кривой, в которых ранг якобиевой матрицы 1 × n равен нулю, т. Е. куда

${\displaystyle f(P)={\frac {\partial f}{\partial x}}(P)={\frac {\partial f}{\partial y}}(P)=0.}$

Особенности кривой не являются бирациональными инвариантами. Однако определение местоположения и классификация особенностей кривой - это один из способов вычисления рода , который является бирациональным инвариантом. Чтобы это сработало, мы должны рассматривать кривую проективно и требовать, чтобы F была алгебраически замкнутой, чтобы были учтены все особенности, принадлежащие кривой.

Классификация особенностей [ править ]

Особые точки включают несколько точек, в которых кривая пересекает саму себя, а также различные типы выступов , например, которые показаны кривой с уравнением x ³  = y ^{2 в} точке (0,0).

Кривая C имеет не более конечного числа особых точек. Если его нет, его можно назвать гладким или неособым . Обычно это определение понимается над алгебраически замкнутым полем и для кривой C в проективном пространстве (т. Е. Полным в смысле алгебраической геометрии). Например, плоская кривая уравнения считается сингулярной, поскольку имеет особую точку (куспид) на бесконечности.${\displaystyle y-x^{3}=0}$

В оставшейся части этого раздела рассматривается плоская кривая C, определяемая как нулевое множество двумерного многочлена f ( x , y ) . Некоторые из результатов, но не все, можно обобщить на неплоские кривые.

Особые точки классифицируются с помощью нескольких инвариантов. Кратность m определяется как максимальное целое число, такое, что производные f для всех порядков до m - 1 обращаются в нуль (также минимальное число пересечения между кривой и прямой в P ). Интуитивно, особая точка имеет дельту - инвариантный б , если она концентрирует δ обычных двойных точек в P . Чтобы сделать это точным, раздутие процесса производит так называемые бесконечно близкие точки , и суммируя м ( м -1) / 2по бесконечно близким точкам, где m - их кратность, дает δ . Для неприводимой и приведенной кривой и точки P мы можем определить δ алгебраически как длину, где - локальное кольцо в P и - его целое замыкание. ^[1]${\displaystyle {\widetilde {{\mathcal {O}}_{P}}}/{\mathcal {O}}_{P}}$${\displaystyle {\mathcal {O}}_{P}}$${\displaystyle {\widetilde {{\mathcal {O}}_{P}}}}$

Число Милнора μ особенности - это степень отображенияград f ( x , y )/| grad  f ( x , y ) |на малой сфере радиуса ε в смысле топологической степени непрерывного отображения , где grad  f - (комплексное) градиентное векторное поле f . Он связан с δ и r формулой Милнора – Юнга :

μ = 2δ - r + 1.

Здесь ветвления числа г из Р есть число локально неприводимых ветви в P . Например, r = 1 на обычном куспиде и r = 2 в обычной двойной точке. Кратность m не меньше r , а P сингулярна тогда и только тогда, когда m не меньше 2. Более того, δ не меньше m ( m -1) / 2.

Вычисление дельта-инвариантов всех особенностей позволяет определить род кривой g ; если d - степень, то

${\displaystyle g={\frac {1}{2}}(d-1)(d-2)-\sum _{P}\delta _{P},}$

где сумма берется по всем особым точкам P комплексной проективной плоской кривой. Это называется формулой рода .

Сопоставим инварианты [ m , δ, r ] особенности, где m - кратность, δ - дельта-инвариант, а r - число ветвления. Тогда обычная точка возврата - это точка с инвариантами [2,1,1], обычная двойная точка - это точка с инвариантами [2,1,2], а обычная m -кратная точка - это точка с инвариантами [ m , m ( м −1) / 2, м ].

Примеры кривых [ править ]

Рациональные кривые [ править ]

Рациональная кривая , которая также называется уникурсальной кривой, любая кривая, бирационально к линии, которые мы можем предпринять , чтобы проективная прямая; соответственно, мы можем отождествить функциональное поле кривой с полем рациональных функций от одной неопределенной F ( x ). Если F алгебраически замкнута, это эквивалентно кривой нулевого рода ; однако поле всех вещественных алгебраических функций, определенных на вещественном алгебраическом многообразии x ² + y ²  = −1, является полем нулевого рода, которое не является полем рациональных функций.

Конкретно, рациональная кривая, вложенная в аффинное пространство размерности n над F, может быть параметризована (за исключением изолированных исключительных точек) с помощью n рациональных функций от одного параметра t ; за счет уменьшения этих рациональных функций к тому же знаменателю, то п + 1 в результате полиномы определяют полином параметризацию от проективное завершения кривой в проективное пространство. Примером может служить рациональная нормальная кривая , где все эти многочлены являются одночленами .

Любое определенное над F коническое сечение с рациональной точкой в F является рациональной кривой. Его можно параметризовать, проведя линию с наклоном t через рациональную точку и пересекающуюся с плоской квадратичной кривой; это дает многочлен с F- рациональными коэффициентами и одним F -рациональным корнем, следовательно, другой корень также является F -рациональным (т. е. принадлежит F ).

Например, рассмотрим эллипс x ² + xy + y ²  = 1, где (−1, 0) - рациональная точка. Проведя линию с наклоном t из (−1,0), y  = t ( x +1), подставив ее в уравнение эллипса, разложив на множители и решив относительно x , получим

${\displaystyle x={\frac {1-t^{2}}{1+t+t^{2}}}.}$

Тогда уравнение для y имеет вид

${\displaystyle y=t(x+1)={\frac {t(t+2)}{1+t+t^{2}}}\,,}$

который определяет рациональную параметризацию эллипса и, следовательно, показывает, что эллипс является рациональной кривой. Даны все точки эллипса, кроме (−1,1), что соответствует t  = ∞; поэтому вся кривая параметризована реальной проективной линией.

Такую рациональную параметризацию можно рассматривать в проективном пространстве , приравнивая первые проективные координаты числителям параметризации, а последние - общему знаменателю. Поскольку параметр определен в проективной линии, многочлены в параметре должны быть усреднены . Например, проективная параметризация вышеуказанного эллипса имеет вид

${\displaystyle X=U^{2}-T^{2},\quad Y=T\,(T+2\,U),\quad Z=T^{2}+TU+U^{2}.}$

Исключая T и U между этими уравнениями, мы снова получаем проективное уравнение эллипса

${\displaystyle X^{2}+X\,Y+Y^{2}=Z^{2},}$

которое можно легко получить непосредственно путем усреднения приведенного выше уравнения.

Многие кривые в списке кривых Википедии являются рациональными и, следовательно, имеют аналогичные рациональные параметризации.

Кривые рациональной плоскости [ править ]

Кривые рациональной плоскости - это рациональные кривые, вложенные в . Для общих сечений однородных по степени многочленов от двух координат , существует отображение${\displaystyle \mathbb {P} ^{2}}$${\displaystyle s_{1},s_{2},s_{2}\in \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))}$${\displaystyle d}$${\displaystyle x,y}$

${\displaystyle s:\mathbb {P} ^{1}\to \mathbb {P} ^{2}}$ данный ${\displaystyle s([x:y])=[s_{1}([x:y]):s_{2}([x:y]):s_{3}([x:y])]}$

определение рациональной плоской кривой степени . ^[2] Существует ассоциированное пространство модулей (где - класс гиперплоскости), параметризующее все такие стабильные кривые . Для определения размерности пространств модулей можно произвести подсчет измерений: есть параметры, указывающие общее количество параметров для каждого из разделов. Тогда, так как они рассматриваются с точностью до проективного фактора в есть меньше параметр . Кроме того, существует трехмерная группа автоморфизмов , следовательно, имеет размерность . Это пространство модулей может быть использовано для подсчета числа от степени рациональных кривых плоскости , пересекающее${\displaystyle d}$ ${\displaystyle {\mathcal {M}}={\overline {\mathcal {M}}}_{0,0}(\mathbb {P} ^{2},d\cdot [H])}$${\displaystyle [H]}$${\displaystyle d+1}$${\displaystyle \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))}$${\displaystyle 3d+3}$${\displaystyle \mathbb {P} ^{2}}$${\displaystyle 1}$${\displaystyle {\mathcal {M}}}$${\displaystyle \mathbb {P} ^{1}}$${\displaystyle {\mathcal {M}}}$${\displaystyle 3d+3-1-3=3d-1}$${\displaystyle N_{d}}$${\displaystyle d}$${\displaystyle 3d-1}$точки с помощью теории Громова – Виттена . ^[3] Он задается рекурсивным соотношением

${\displaystyle N_{d}=\sum _{d_{A}+d_{B}=d}N_{d_{A}}N_{d_{B}}d_{A}^{2}d_{B}\left(d_{B}{\binom {3d-4}{3d_{A}-2}}-d_{A}{\binom {3d-4}{3d_{A}-1}}\right)}$

где .${\displaystyle N_{1}=N_{2}=1}$

Эллиптические кривые [ править ]

Эллиптической кривой может быть определен как любой кривой рода один с рациональной точки : общая модель представляет собой неособый кубической кривой , что достаточно для моделирования произвольного рода одной кривой. В этой модели выделенная точка обычно считается точкой перегиба на бесконечности; это означает, что кривая может быть записана в форме Тейта-Вейерштрасса, которая в своей проективной версии имеет вид

${\displaystyle y^{2}z+a_{1}xyz+a_{3}yz^{2}=x^{3}+a_{2}x^{2}z+a_{4}xz^{2}+a_{6}z^{3}.}$

Если характеристика поля отличается от 2 и 3, то линейное изменение координат позволяет положить, что дает классическую форму Вейерштрасса${\displaystyle a_{1}=a_{2}=a_{3}=0,}$

${\displaystyle y^{2}=x^{3}+px+q.}$

Эллиптические кривые несут структуру абелевой группы с выделенной точкой как тождество группового закона. В плоской кубической модели сумма трех точек в группе равна нулю тогда и только тогда, когда они коллинеарны . Для эллиптической кривой, определенной над комплексными числами, группа изоморфна аддитивной группе комплексной плоскости по модулю решетки периодов соответствующих эллиптических функций .

Пересечение двух квадратичных поверхностей , как правило, представляет собой неособую кривую рода один и степени четыре и, следовательно, эллиптическую кривую, если у нее есть рациональная точка. В особых случаях пересечение может быть либо рациональной особой квартикой, либо разложено на кривые меньшей степени, которые не всегда различны (либо кубическая кривая и линия, либо две коники, либо коника и две прямые, либо четыре прямые) .

Кривые рода больше единицы [ править ]

Кривые рода больше единицы заметно отличаются как от рациональных, так и от эллиптических кривых. Такие кривые, определенные над рациональными числами, согласно теореме Фалтингса , могут иметь только конечное число рациональных точек, и их можно рассматривать как имеющие структуру гиперболической геометрии . Примерами являются гиперэллиптические кривые , кривая квартики Клейна и кривая Ферма x ⁿ  +  y ⁿ  = z ^n, когда n больше трех. Кроме того, проективные плоские кривые в и кривые в предоставляют множество полезных примеров.${\displaystyle \mathbb {P} ^{2}}$${\displaystyle \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$

Кривые на проекционной плоскости [ править ]

Плоские кривые степени , которые могут быть построены как множество исчезающих общего сечения , имеют род${\displaystyle C\subset \mathbb {P} ^{2}}$${\displaystyle k}$${\displaystyle s\in \Gamma (\mathbb {P} ^{2},{\mathcal {O}}(k))}$

${\displaystyle {\frac {(k-1)(k-2)}{2}}}$

которые можно вычислить с помощью когомологий когерентных пучков . Вот краткое изложение родов кривых в зависимости от их степени.

${\displaystyle {\begin{matrix}{\text{degree}}&1&2&3&4&5&6&7\\{\text{genus}}&0&0&1&3&6&10&15\end{matrix}}}$

Например, кривая определяет кривую рода, которая является гладкой, поскольку дифференциалы не имеют общих нулей с кривой. Не примером общего сечения является кривая, которая, согласно теореме Безаута , должна пересекаться в большинстве точек, является объединение двух рациональных кривых, пересекающихся в двух точках. Замечание дается обращающимся в нуль геометрическим вектором и задается исчезающим геометрическим вектором . Их можно найти явно: точка лежит в обоих if . Итак, два решения - это такие точки , которые есть и .${\displaystyle x^{4}+y^{4}+z^{4}}$${\displaystyle 3}$${\displaystyle 4x^{3},4y^{3},4z^{3}}$${\displaystyle x(x^{2}+y^{2}+z^{2})}$${\displaystyle 2}$${\displaystyle C_{1}\cup C_{2}}$${\displaystyle C_{1}}$${\displaystyle x}$${\displaystyle C_{2}}$${\displaystyle x^{2}+y^{2}+z^{2}}$${\displaystyle x=0}$${\displaystyle [0:y:z]}$${\displaystyle y^{2}+z^{2}=0}$${\displaystyle [0:1:-1]}$${\displaystyle [0:1:{\sqrt {-1}}]}$

Кривые в произведении проективных линий [ править ]

Кривая, заданная множеством исчезающих точек , для дает кривые рода${\displaystyle C\subset \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$${\displaystyle s\in \Gamma (\mathbb {P} ^{1}\times \mathbb {P} ^{1},{\mathcal {O}}(a,b))}$${\displaystyle a,b\geq 2}$

${\displaystyle ab-a-b+1}$

что можно проверить с помощью когомологий когерентных пучков . Если , то они определяют кривые рода , следовательно, кривую любого рода можно построить как кривую в . Их роды можно свести в таблице.${\displaystyle a=2}$${\displaystyle 2b-2-b+1=b-1}$${\displaystyle \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$

${\displaystyle {\begin{matrix}{\text{bidegree}}&(2,2)&(2,3)&(2,4)&(2,5)\\{\text{genus}}&1&2&3&4\end{matrix}}}$

и для этого${\displaystyle a=3}$

${\displaystyle {\begin{matrix}{\text{bidegree}}&(3,2)&(3,3)&(3,4)&(3,5)\\{\text{genus}}&2&4&6&8\end{matrix}}}$

См. Также [ править ]

Классическая алгебраическая геометрия [ править ]

Современная алгебраическая геометрия [ править ]

Геометрия римановых поверхностей [ править ]

Примечания [ править ]

Ссылки [ править ]

Викискладе есть медиафайлы, связанные с алгебраическими кривыми .

• Эгберт Брискорн и Хорст Кнёррер , Плоские алгебраические кривые , Джон Стиллвелл , переводчик, Биркхойзер , 1986
• Клод Шевалле , Введение в теорию алгебраических функций одной переменной , Американское математическое общество , Математические обзоры номер VI, 1951 г.
• Дж. Л. Кулидж , Трактат об алгебраических плоских кривых , издательство Oxford University Press , 1931 г. ( Dover Publications 2004).
• Хершель М. Фаркас и Ирвин Кра, Римановы поверхности , Springer, 1980.
• В. Фултон, Алгебраические кривые: введение в алгебраическую геометрию .
• К.Г. Гибсон, Элементарная геометрия алгебраических кривых: Введение для студентов , Cambridge University Press , 1998.
• Филип А. Гриффитс , Введение в алгебраические кривые , Кунико Велтин, перевод, Американское математическое общество, Перевод математических монографий, том 70, редакция 1985 г.
• Робин Хартшорн , Алгебраическая геометрия , Springer, 1977
• Сигеру Иитака , Алгебраическая геометрия: Введение в бирациональную геометрию алгебраических многообразий , Springer, 1982
• Джон Милнор , Особые точки сложных гиперповерхностей , Princeton University Press , 1968
• Джордж Сэлмон , Кривые на высших плоскостях , третье издание, GE Stechert & Co., 1934 г.
• Жан-Пьер Серр , Алгебраические группы и поля классов , Springer, 1988 г.
• Эрнст Кёттер (1887 г.). "Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Kurven (Основы чисто геометрической теории алгебраических плоских кривых)". Труды Королевской академии Берлина .- получил приз Академии 1886 года ^[1]