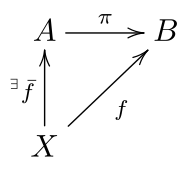Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску

В математике , А проекция является отображение множества (или другой математической структуры ) в подмножество (или суб-структуры), которая равна квадрату ее для композиции отображения (или, другими словами, что является идемпотентная ). Ограничение на подпространство проекции также называется проекцией, даже если свойство идемпотентности потеряно. Обычный пример проекции - отбрасывание тени на плоскость (лист бумаги). Проекция точки - это ее тень на листе бумаги. Тень точки на листе бумаги и есть сама эта точка (идемпотентность). Тень трехмерной сферы - это замкнутый диск. Первоначально понятие проекции было введено в евклидовой геометрии для обозначения проекции трехмерного евклидова пространства на плоскость в нем, как в примере с тенью. Двумя основными прогнозами такого рода являются:

  • Проекция из точки на плоскость или центральной проекции : Если С является точкой, которая называется центром проекции , то проекция точки P отличается от C на плоскость , которая не содержит C представляет собой пересечение линии CP с самолет. Точки P, такие, что прямая CP параллельна плоскости, не имеют никакого изображения проекцией, но часто говорят, что они проецируются в бесконечно удаленную точку плоскости (см. Проективную геометрию для формализации этой терминологии). Проекция точки C сам не определяется.
  • Проекция параллельно направлению D, на плоскость или параллельной проекции : изображение точки Р есть пересечение с плоскостью линии , параллельной D , проходящей через P . См. Аффинное пространство § Проекция для получения точного определения, обобщенного для любого измерения.

Концепция проекции в математике очень старая, скорее всего, уходит своими корнями в феномен теней, отбрасываемых реальными объектами на земле. Эта элементарная идея была уточнена и абстрагирована сначала в геометрическом контексте, а затем в других разделах математики. Со временем развивались разные версии концепции, но сегодня, в достаточно абстрактной обстановке, мы можем объединить эти варианты.

В картографии , А проекция является картой части поверхности Земли на плоскость, которая, в некоторых случаях, но не всегда, является ограничением проекции в указанном выше смысле. В 3D - проекции также на основе теории перспективы .

Необходимость объединения двух видов проекций и определения изображения центральной проекцией любой точки, отличной от центра проекции, лежит в основе проективной геометрии . Однако проективное преобразование - это биекция проективного пространства, свойство, не разделяемое с проекциями в этой статье.

Определение [ править ]

Коммутативность этой диаграммы - это универсальность проекции π для любого отображения f и множества X.

В абстрактном контексте мы обычно можем сказать, что проекция - это отображение набора (или математической структуры ), которое является идемпотентным , что означает, что проекция равна своей композиции с самим собой. Проекция может также относиться к отображению , которое имеет правый обратный. Оба понятия тесно связаны между собой следующим образом. Пусть p - идемпотентное отображение множества A в себя (таким образом, p  ∘ p  = p ) и B  = p ( A ) - образ p. Если мы обозначим через П отображение р рассматривается как отображение из A на B и I в инъекции из B в A (так , что р  = я  ∘ л ), то мы имеем П  ∘ я  = Id Б (так что л имеет правая обратная). Наоборот, если π имеет правый обратный, то π  ∘  i = Id B влечет, что i  ∘ π идемпотентно.

Приложения [ править ]

Первоначальное понятие проекции было расширено или обобщено на различные математические ситуации, часто, но не всегда, связанные с геометрией, например:

  • В теории множеств :
    • Операция, типизированная j-  й картой проекции , обозначаемой как proj j  , которая берет элемент x = ( x 1 , ..., x j  , ..., x k ) декартового произведения X 1 ×… × X j × … × X k к значению proj j  ( x ) = x j  . Эта карта всегда сюръективна .
    • Отображение, которое переводит элемент в его класс эквивалентности при заданном отношении эквивалентности, называется канонической проекцией .
    • Карта оценки отправляет функцию f в значение f ( x ) для фиксированного x . Пространство функций Y X можно отождествить с декартовым произведением , а оценочная карта - это карта проекции из декартова произведения.
  • Для реляционных баз данных и запросов языков , то проекция является унарной операция записывается в виде , где есть множество имен атрибутов. Результат такой проекции определяется как набор, который получается, когда все кортежи в R ограничены набором . R - отношение базы данных .
  • В сферической геометрии проекция сферы на плоскость использовалась Птолемеем (~ 150) в его Planisphaerium . Этот метод называется стереографической проекцией и использует касательную плоскость к сфере и полюс C, диаметрально противоположный точке касания. Любая точка P на сфере , кроме C определяет линию CP , пересекающую плоскость на проектируемой точки для P . Соответствие делает сферу компактификацией одной точки для плоскости, когда точка на бесконечности включена, чтобы соответствовать C, который в противном случае не имеет проекции на плоскость. Обычным примером является комплексная плоскость, где компактификация соответствует сфере Римана . В качестве альтернативы, полусфера часто проецируется на плоскость с помощью гномонической проекции .
  • В линейной алгебре - линейное преобразование, которое остается неизменным при двукратном применении ( p ( u ) = p ( p ( u ))), другими словами, идемпотентный оператор. Например, отображение, которое переводит точку ( x , y , z ) в трех измерениях в точку ( x , y , 0) на плоскости, является проекцией. Этот тип проекции естественным образом обобщается на любое количество измерений n для источника и k ≤ n для цели отображения. Видетьортогональная проекция , проекция (линейная алгебра) . В случае ортогональных проекций пространство допускает разложение как произведение, и оператор проекции также является проекцией в этом смысле.
  • В дифференциальной топологии любой пучок волокон включает карту проекции как часть своего определения. По крайней мере, локально эта карта выглядит как проекционная карта в смысле топологии продукта и поэтому является открытой и сюръективной.
  • В топологии , А втягивании непрерывного отображения г : Х → Х , который ограничивает к карте идентичности на ее изображение. Это удовлетворяет аналогичному условию идемпотентности r 2 = r и может рассматриваться как обобщение карты проекции. Изображение ретракции называется ретрактом исходного пространства. Втягивание, гомотопное идентичности, называется ретракцией деформации . Этот термин также используется в теории категорий для обозначения любого расщепленного эпиморфизма.
  • Скалярная проекция (или решительный) одного вектора на другой.
  • В теории категорий указанное выше понятие декартова произведения множеств можно обобщить на произвольные категории . Продукт некоторых объектов имеет каноническую проекцию морфизм для каждого фактора. Эта проекция примет множество форм в разных категориях. Проекция из декартово произведения из множеств , то топология произведения из топологических пространств (который всегда сюръективна и открыта ), или из прямого произведения из групп и т.д. Хотя эти морфизмы часто эпиморфизмы и даже сюръективными они не должны быть.

Дальнейшее чтение [ править ]

  • Томас Крейг (1882) Трактат о прогнозах из Исторического математического собрания Мичиганского университета .