Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску

В теории множеств , то Шредер-Бернштейн теорема утверждает , что, если существуют инъективные функции F  : A → B и г  : B → A между множествами A и B , то существует взаимно однозначное функцию час  : A → B .

С точки зрения мощности двух множеств это классически означает, что если | А | ≤ | B | и | B | ≤ | А | , тогда | А | = | B | ; то есть, и B являются равносильными . Это полезная функция для упорядочивания количественных чисел .

Теорема названа в честь Феликса Бернштейна и Эрнста Шредера . Она также известна как теорема Кантора – Бернштейна или Кантора – Шредера – Бернштейна в честь Георга Кантора, который впервые опубликовал ее без доказательства.

Доказательство [ править ]

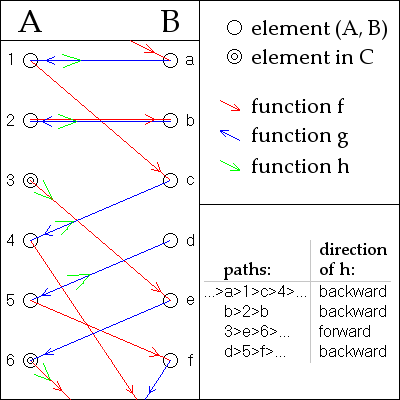
Определение Konig по биекция ч :  →  B из приведенного примера инъекций F : A  →  B и г : B  →  A . Элемент в A и B обозначается цифрой и буквой соответственно. Последовательность 3 → e → 6 → ... является A- стопором, что приводит к определениям h (3) =  f (3) =  e , h (6) =  f (6), .... Последовательность d  → 5 →  f  → ... это B-стоппер, ведущий к h (5) =  g −1 (5) =  d , .... Последовательность ... →  a  → 1 →  c  → 4 → ... вдвойне бесконечна, что приводит к h (1) =  g −1 (1) =  a , h (4) =  g −1 (4) =  c , .... Последовательность b  → 2 →  b циклическая, что приводит к h (2) =  g −1 (2 ) =  b .

Следующее доказательство приписывается Юлиусу Кенигу . [1]

Без ограничения общности предположим, что A и B не пересекаются . Для любого a в A или b в B мы можем сформировать уникальную двустороннюю последовательность элементов, которые поочередно находятся в A и B , многократно применяя и для перехода от A к B и и для перехода от B к A (где определено; обратные и понимаются как частичные функции на этой стадии пуфа.)

Для любого конкретного a эта последовательность может заканчиваться слева или нет, в точке, где или не определена.

Поскольку и являются инъективными функциями, каждый a в A и b в B находится ровно в одной такой последовательности с точностью до идентичности: если элемент встречается в двух последовательностях, все элементы слева и справа должны быть одинаковыми в обоих , по определению последовательностей. Таким образом, последовательности образуют перегородку из (непересекающихся) объединение A и B . Следовательно, достаточно произвести взаимно однозначное соответствие между элементами A и B в каждой из последовательностей отдельно, как показано ниже:

Назовем последовательность в A-пробку , если она останавливается на элементе A или B-стопора , если он останавливается на элемент B . В противном случае назовите его вдвойне бесконечным, если все элементы различны, или циклическим, если он повторяется. Примеры смотрите на картинке.

  • Для A-пробки , функция является взаимно однозначным соответствием между его элементами в А и его элементах в B .
  • Для B-пробки , функция является взаимно однозначным соответствием между ее элементами B и ее элементами в A .
  • Для дважды бесконечной последовательности или циклической последовательности подойдет либо или ( используется на рисунке).

История [ править ]

Традиционное название «Шредер-Бернштейн» основано на двух доказательствах, опубликованных независимо в 1898 году. Кантора часто добавляют, потому что он впервые сформулировал теорему в 1887 году, в то время как имя Шредера часто опускается, потому что его доказательство оказалось ошибочным, в то время как имя Ричарда Дедекинд , первым доказавший это, не имеет отношения к теореме. Согласно Бернштейну, Кантор предложил теорему эквивалентности имен (Äquivalenzsatz). [2]

Первое утверждение теоремы Кантора (1887 г.) [3]
  • 1887 Кантор публикует теорему, но без доказательства. [3] [2]
  • 1887 г. 11 июля Дедекинд доказывает теорему (не полагаясь на аксиому выбора ) [4], но не публикует свое доказательство и не сообщает о нем Кантору. Эрнст Цермело открыл доказательство Дедекинда и в 1908 году [5] публикует собственное доказательство, основанное на теории цепей из статьи Дедекинда. Was sind und was sollen die Zahlen? [2] [6]
  • 1895 г. Кантор формулирует теорему в своей первой статье по теории множеств и трансфинитным числам. Он получает это как простое следствие линейного порядка кардинальных чисел. [7] [8] [9] Тем не менее, он не мог доказать последнюю теорему, которая показана в 1915 году , чтобы быть эквивалентна аксиоме выбора с помощью Фридриха Moritz Гартогсом . [2] [10]
  • 1896 г. Шредер объявляет доказательство (как следствие теоремы Джевонса ). [11]
  • 1897 г. Бернштейн , 19-летний студент семинара Кантора, представляет свое доказательство. [12] [13]
  • 1897 г. Почти одновременно, но независимо, Шредер находит доказательство. [12] [13]
  • 1897 г. После визита Бернштейна Дедекинд независимо доказывает теорему во второй раз.
  • 1898 Доказательство Бернштейна (не опирающееся на аксиому выбора) публикуется Эмилем Борелем в его книге о функциях. [14] (Сообщение Кантора на Международном конгрессе математиков 1897 года в Цюрихе). В том же году доказательство также появляется в диссертации Бернштейна . [15] [2]
  • 1898 Шредер публикует свое доказательство [16], которое, однако, было показано Алвином Рейнхольдом Корсельтом в 1902 году (незадолго до смерти Шредера), [17] (подтверждено Шредером), [2] [18], но опубликована статья Корсельта. только в 1911 г.

Оба доказательства Дедекинда основаны на его знаменитых мемуарах 1888 года Was sind und was sollen die Zahlen? и вывести его как следствие предложения, эквивалентного утверждению C из статьи Кантора [7], которое читается как A  ⊆  B  ⊆  C и | А | = | C | подразумевает | А | = | B | = | C |, Кантор наблюдал это свойство еще в 1882/83 году во время своих исследований теории множеств и трансфинитных чисел и поэтому (неявно) полагался на Аксиому выбора .

Предпосылки [ править ]

Доказательство Кантора 1895 г. основывалось на избранной аксиоме , выводя результат как следствие теоремы о хорошем порядке . [8] [9] Однако приведенное выше доказательство Кенига показывает, что результат можно доказать и без использования аксиомы выбора.

С другой стороны, в доказательстве Кенига для анализа случаев используется принцип исключенного третьего, поэтому это доказательство не работает в конструктивной теории множеств . Более того, никакое доказательство не может существовать только на основе одной конструктивной теории множеств (т. Е. Без принципа исключенного третьего), поскольку теорема Шредера – Бернштейна подразумевает принцип исключенного третьего. [19] Следовательно, интуиционисты не принимают теорему. [20]

Существует также доказательство, использующее теорему Тарского о неподвижной точке . [21]

См. Также [ править ]

  • Теорема об изоморфизме Майхилла
  • Теорема Шредера – Бернштейна для измеримых пространств.
  • Теоремы Шредера – Бернштейна для операторных алгебр
  • Свойство Шредера – Бернштейна

Заметки [ править ]

  1. Перейти ↑ J. König (1906). "Sur la théorie des ensembles" . Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences . 143 : 110–112.
  2. ^ a b c d e f Феликс Хаусдорф (2002), Эгберт Брискорн ; Сришти Д. Чаттерджи; и другие. (ред.), Grundzüge der Mengenlehre (1-е изд.), Берлин / Гейдельберг: Springer, стр. 587, ISBN 978-3-540-42224-2- Оригинальное издание (1914 г.)
  3. ^ a b Георг Кантор (1887), "Mitteilungen zur Lehre vom Transfiniten", Zeitschrift für Philosophie und Philosophische Kritik , 91 : 81–125
    Перепечатано в: Георг Кантор (1932), Адольф Френкель (Lebenslauf); Эрнст Цермело (ред.), Gesammelte Abhandlungen Mathematischen und Philophischen Inhalts , Берлин: Springer, стр. 378–439. Здесь: стр.413 внизу
  4. ^ Ричард Дедекинд (1932), Роберт Фрике ; Эмми Нётер; Øystein Ore (ред.), Gesammelte Mathematische Werke , 3 , Брауншвейг: Friedr. Vieweg & Sohn, стр. 447–449 (Глава 62)
  5. ^ Эрнст Цермело (1908), Феликс Кляйн; Вальтер фон Дейк ; Дэвид Гильберт; Отто Блюменталь (ред.), "Untersuchungen über умереть Grundlagen дер Mengenlehre I" , Mathematische Annalen , 65 (2): 261-281, здесь: p.271-272, DOI : 10.1007 / bf01449999 , ISSN 0025-5831 
  6. ↑ Ричард Дедекинд (1888 г.), « Был ли злодей Зален? (2., без изменений (1893) изд.), Брауншвейг: Friedr. Vieweg & Sohn
  7. ^ а б Георг Кантор (1932), Адольф Френкель (Lebenslauf); Эрнст Цермело (ред.), Gesammelte Abhandlungen Mathematischen und Philophischen Inhalts , Берлин: Springer, стр. 285 ("Satz B")
  8. ^ а б Георг Кантор (1895). "Beiträge zur Begründung der transfiniten Mengenlehre (1)" . Mathematische Annalen . 46 (4): 481–512 (теорему см. "Satz B", с.484). DOI : 10.1007 / bf02124929 .
  9. ^ a b ( Георг Кантор (1897). «Beiträge zur Begründung der transfiniten Mengenlehre (2)» . Mathematische Annalen . 49 (2): 207–246. doi : 10.1007 / bf01444205 .)
  10. ↑ Фридрих М. Хартогс (1915), Феликс Кляйн; Вальтер фон Дейк; Дэвид Гильберт; Отто Блюменталь (ред.), "Über das Problem der Wohlordnung" , Mathematische Annalen , 76 (4): 438–443, doi : 10.1007 / bf01458215 , ISSN 0025-5831 
  11. ^ Эрнст Шредер (1896). "Убер Г. Канторше Сатце" . Jahresbericht der Deutschen Mathematiker-Vereinigung . 5 : 81–82.
  12. ^ a b Оливер Дайзер (2010), Einführung in die Mengenlehre - Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo , Springer-Lehrbuch (3-е, исправленное издание), Берлин / Гейдельберг: Springer, стр. 71, 501, doi : 10.1007 / 978-3-642-01445-1 , ISBN 978-3-642-01444-4
  13. ^ a b Патрик Суппес (1972), Теория аксиоматических множеств (1-е изд.), Нью-Йорк: Dover Publications, стр.  95 f , ISBN 978-0-486-61630-8
  14. ↑ Эмиль Борель (1898), Leçons sur la théorie des fonctions , Париж: Gauthier-Villars et fils, стр. 103 и далее.
  15. ^ Феликс Бернштейн (1901), Untersuchungen AUS - дер - Mengenlehre , Halle а. С .: Buchdruckerei des Waisenhauses
    Перепечатано в: Феликс Бернштейн (1905), Феликс Кляйн; Вальтер фон Дейк; Давид Гильберт (ред.), "Untersuchungen AUS - дер - Mengenlehre" , Mathematische Annalen , 61 (1): 117-155, (теорема см "Satz 1" на с.121), DOI : 10.1007 / bf01457734 , ISSN 0025-5831 
  16. ^ Эрнст Шредер (1898), Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher (ed.), "Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze" , Nova Acta , 71 (6): 303–376 (доказательство: стр. .336–344)
  17. ^ Алвин Р. Корселт (1911), Феликс Кляйн; Вальтер фон Дейк; Дэвид Гильберт; Отто Блюменталь (ред.), "Uber einen Beweis des Äquivalenzsatzes" , Mathematische Annalen , 70 (2): 294–296, doi : 10.1007 / bf01461161 , ISSN 0025-5831 
  18. ^ Korselt (1911), p.295
  19. ^ Прадич, Пьер; Браун, Чад Э. (2019). «Кантор-Бернштейн подразумевает исключенное среднее». arXiv : 1904.09193 [ math.LO ].
  20. ^ Этторе Карруччо (2006). Математика и логика в истории и современной мысли . Издатели транзакций. п. 354. ISBN 978-0-202-30850-0.
  21. ^ Р. Уль, « Теорема Тарского о неподвижной точке », из MathWorld - веб-ресурса Wolfram, созданного Эриком У. Вайстейном. (Пример 3)

Ссылки [ править ]

  • Мартин Айгнер и Гюнтер М. Циглер (1998) Доказательства из КНИГИ , § 3 Анализ: Множества и функции, Книги Springer MR 1723092 , пятое издание 2014 MR 3288091 , шестое издание 2018 MR 3823190
  • Хинкис, Ари (2013), Доказательства теоремы Кантора-Бернштейна. Математический экскурс в Science Networks. Исторические исследования, 45 , Гейдельберг: Birkhäuser / Springer, DOI : 10.1007 / 978-3-0348-0224-6 , ISBN 978-3-0348-0223-9, MR  3026479
  • Searcóid, Míchaél Ó (2013). «К истории и математике теоремы эквивалентности». Математические материалы Ирландской королевской академии . 113A : 151–68. DOI : 10,3311 / PRIA.2013.113.14 . JSTOR  42912521 .

Внешние ссылки [ править ]

  • Вайсштейн, Эрик В. «Теорема Шредера-Бернштейна» . MathWorld .
  • Теорема Кантора-Шредера-Бернштейна в nLab
  • Теорема Кантора-Бернштейна о полукольце Марселя Краббе.
  • Эта статья включает материал из статьи Citizendium " Schröder-Bernstein_theorem ", которая находится под лицензией Creative Commons Attribution-ShareAlike 3.0 Unported License, но не GFDL .