Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску

В математике есть два конкурирующих определения кирального многогранника . Во- первых, это многогранник , который является хиральным (или «энантиоморфных»), что означает , что он не имеет зеркальную симметрию . Согласно этому определению, многогранник, который вообще лишен какой-либо симметрии, был бы примером кирального многогранника.

Другое, конкурирующее определение кирального многогранника состоит в том, что это многогранник, который является максимально симметричным, но не зеркально-симметричным, формализованным в терминах действия группы симметрии многогранника на его флаги . Согласно этому определению даже высокосимметричные и энантиоморфные многогранники, такие как курносый куб , не являются киральными. Из-за нехватки геометрических примеров большая часть исследований симметричных, но киральных многогранников проводилась в рамках абстрактных многогранников .

Многогранники без зеркальной симметрии [ править ]

Разносторонний треугольник не имеет зеркальной симметрии и, следовательно, является хиральным в 2-х измерениях.
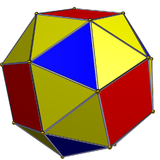Snub hexahedron.pngКурносый шестигранник ccw.png
Курносый куб , вершина-транзитивное , но не зеркально-симметрично.

Многим многогранникам не хватает зеркальной симметрии, и в этом смысле они образуют киральные многогранники. Самый простой пример - разносторонний треугольник . [1]

Многогранники могут иметь высокую степень симметрии, но при этом не иметь зеркальной симметрии; простой пример - дисфеноид, когда его грани не конгруэнтны равнобедренному треугольнику ; [2] другим примером является курносый куб , который в этом смысле является вершинно-транзитивным и киральным. [3]

Симметричные киральные многогранники [ править ]

Определение [ править ]

Более техническое определение кирального многогранника - это многогранник, у которого есть две орбиты флагов под своей группой симметрий , со смежными флагами на разных орбитах. Это означает, что он должен быть вершинно-транзитивным , реберно-транзитивным и гранным , поскольку каждая вершина, ребро или грань должны быть представлены флагами на обеих орбитах; однако он не может быть зеркально-симметричным, поскольку каждая зеркальная симметрия многогранника поменяла бы некоторую пару соседних флагов. [4]

Для целей этого определения группа симметрии многогранника может быть определена одним из двух различных способов: она может относиться к симметриям многогранника как геометрического объекта (в этом случае многогранник называется геометрически киральным ) или он может назовем симметрии многогранника комбинаторной структурой ( абстрактным многогранником ). Хиральность имеет значение для любого типа симметрии, но эти два определения классифицируют разные многогранники как киральные или нехиральные. [5]

В трех измерениях [ править ]

В трехмерном пространстве геометрически киральный многогранник не может иметь конечное число конечных граней. Например, курносый куб является вершинно-транзитивным, но его флаги имеют более двух орбит, и он не является ни рёберно-транзитивным, ни грань-транзитивным, поэтому он недостаточно симметричен, чтобы соответствовать формальному определению киральности. Квазирегулярная многогранники и двойственные, такие как кубооктаэдр и ромбический додекаэдр , обеспечивают еще один интересный типа ближнего промаха: у них есть две орбит флагов, но зеркально симметрично, и не каждая смежная пара флагов принадлежит различным орбитам. Однако, несмотря на отсутствие конечных киральных трехмерных многогранников, существуют бесконечные трехмерные киральные косые многогранникитипов {4,6}, {6,4} и {6,6}. [5]

Ссылки [ править ]

  1. ^ Тилли, Ричард JD (2006), Кристаллы и кристаллические структуры , John Wiley & Sons, стр. 44, ISBN 9780470018217.
  2. ^ Петижан, М. (2015). «Самый хиральный дисфеноид» (PDF) . MATCH - Связь по математике и компьютерной химии . 73 (2): 375–384. Zbl 06749519 .  CS1 maint: Zbl ( ссылка )
  3. ↑ Coxeter, HSM (1995), Калейдоскопы: Избранные сочинения , John Wiley and Sons, p. 282, ISBN 9780471010036.
  4. ^ Шульте, Эгон ; Weiss, Asia Ivić (1991), «Хиральные многогранники», в Gritzmann, P .; Sturmfels, B. (eds.), Applied Geometry and Discrete Mathematics (The Victor Klee Festschrift) , Серия DIMACS по дискретной математике и теоретической информатике, 4 , Провиденс, Род-Айленд: Американское математическое общество, стр. 493–516, MR 1116373 .
  5. ^ a b Шульте, Эгон (2004), «Киральные многогранники в обычном пространстве. I» (PDF) , Дискретная и вычислительная геометрия , 32 (1): 55–99, DOI : 10.1007 / s00454-004-0843-x , MR 2060817 , S2CID 13098983 , архивируются от оригинала (PDF) на 2010-11-17 , извлекаются 2012-09-01    .

Дальнейшее чтение [ править ]

  • Монсон, Барри; Писанский, Томаж ; Шульте, Эгон; Вайс, Азия Ивич (2007), «Полусимметричные графы из многогранников», Журнал комбинаторной теории , серия A, 114 (3): 421–435, arXiv : math / 0606469 , doi : 10.1016 / j.jcta.2006.06.007 , Руководство по ремонту  2310743 , S2CID  10203794.
  • Хабард, Изабель; Вайс, Азия Ивич (2005), «Самодуальность киральных многогранников», Журнал комбинаторной теории , серия A, 111 (1): 128–136, DOI : 10.1016 / j.jcta.2004.11.012 , MR  2144859.
  • Кондер, Марстон ; Хабард, Изабель; Pisanski, Tomaž (2008), "Конструкция для хиральных многогранников", журнал Лондонского математического общества , вторая серия, 77 (1): 115-129, DOI : 10,1112 / jlms / jdm093 , MR  2389920.
  • Монсон, Барри; Ivić Вайс, Азии (2008), "графы Кэли и симметричные 4-многогранники" , Ars Mathematica Contemporanea , 1 (2): 185-205, DOI : 10,26493 / 1855-3974.79.919 , MR  2466196.