Курносый куб

Эта статья включает в себя список общих ссылок , но он остается в значительной степени непроверенным, поскольку в нем отсутствует достаточное количество соответствующих встроенных ссылок . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Январь 2012 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Курносый куб
(Нажмите здесь, чтобы повернуть модель)
Тип	Архимедово твердое тело равномерный многогранник
Элементы	F = 38, E = 60, V = 24 (χ = 2)
Лица по сторонам	(8 + 24) {3} +6 {4}
Обозначение Конвея	СК
Символы Шлефли	sr {4,3} или ${\ displaystyle s {\ begin {Bmatrix} 4 \\ 3 \ end {Bmatrix}}}$
Символы Шлефли	ht _0,1,2 {4,3}
Символ Wythoff	\| 2 3 4
Диаграмма Кокстера
Группа симметрии	О ,1/2B ₃ , [4,3] ⁺ , (432), порядок 24
Группа вращения	O , [4,3] ⁺ , (432), порядок 24
Двугранный угол	3-3: 153 ° 14′04 ″ (153,23 °) 3-4: 142 ° 59′00 ″ (142,98 °)
Рекомендации	U ₁₂ , C ₂₄ , W ₁₇
Характеристики	Полуправильная выпуклая киральная
Цветные лица	3.3.3.3.4 ( фигура вершины )
Пятиугольный икоситетраэдр ( двойственный многогранник )	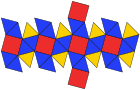Сеть

3D модель курносого куба

В геометрии , в курносой кубе , или курносого кубооктаэдре , является архимедовым твердым веществом с 38 гранями: 6 квадратов и 32 равносторонних треугольниками . У него 60 ребер и 24 вершины .

Это киральный многогранник; то есть он имеет две различные формы, которые являются зеркальным отображением (или « энантиоморфами ») друг друга. Объединение обеих форм представляет собой соединение двух плоских кубов , а выпуклая оболочка обоих наборов вершин представляет собой усеченный кубооктаэдр .

Кеплер впервые назвал его на латыни как cubus simus в 1619 году в своей книге « Harmonices Mundi» . Коксетер , отметив , что она может быть получена в равной степени октаэдра , как куб, называет его пренебрежительно кубооктаэдр , с вертикальным расширенным символом Шлефл , и представляет собой чередование о наличии усеченного кубооктаэдра , который имеет символ Шлефл . ${\ displaystyle s \ scriptstyle {\ begin {Bmatrix} 4 \\ 3 \ end {Bmatrix}}}$ ${\ Displaystyle т \ scriptstyle {\ begin {Bmatrix} 4 \\ 3 \ end {Bmatrix}}}$

Размеры [ править ]

Для курносого куба с длиной ребра 1 его площадь поверхности и объем равны:

{\ displaystyle {\ begin {align} A & = 6 + 8 {\ sqrt {3}} && \ приблизительно 19.856 \, 406 \, 460 \, 6 \\ V & = {\ frac {8t + 6} {3 {\ sqrt {2 (t ^ {2} -3)}}}} && \ приблизительно 7.889 \, 477 \, 399 \, 98 \ end {выровнено}}}

где t - постоянная трибоначчи

{\ displaystyle t = {\ frac {1 + {\ sqrt [{3}] {19-3 {\ sqrt {33}}}} + {\ sqrt [{3}] {19 + 3 {\ sqrt {33} }}}}} {3}} \ примерно 1.839 \, 286 \, 755 \, 21.}

Если исходный курносый куб имеет длину ребра 1, его двойной пятиугольный икоситетраэдр имеет длину сторон

{\frac {1}{\sqrt {t+1}}}{\approx 0.593\,465}\quad {\text{and}}\quad {\frac {\sqrt {t+1}}{2}}\approx 0.842\,509.

.

В общем, объем курносого куба с длиной стороны может быть найден по этой формуле, используя t в качестве константы трибоначчи выше: ^[1] $a$

$V=a^{3}\cdot {\frac {3{\sqrt {t-1}}+4{\sqrt {t+1}}}{3{\sqrt {2-t}}}}\approx 7.889\,477\,399\,98a^{3}$ .

Декартовы координаты [ править ]

Декартовы координаты для вершин из курносой кубы все четные подстановок из

(± 1, ±1т, ± t )

с четным числом знаков плюс, наряду со всеми нечетными перестановками с нечетным числом знаков плюс, где t ≈ 1,83929 - константа трибоначчи . Если взять четные перестановки с нечетным числом знаков плюс и нечетные перестановки с четным числом знаков плюс, получится другой пренебрежительный куб, зеркальное отображение. Взяв их все вместе, мы получим соединение двух плоских кубиков .

У этого курносого куба есть ребра длины , число, которое удовлетворяет уравнению $\alpha ={\sqrt {2+4t-2t^{2}}}$

\alpha ^{6}-4\alpha ^{4}+16\alpha ^{2}-32=0,\,

и может быть записано как

{\begin{aligned}\alpha &={\sqrt {{\frac {4}{3}}-{\frac {16}{3\beta }}+{\frac {2\beta }{3}}}}\approx 1.609\,72\\\beta &={\sqrt[{3}]{26+6{\sqrt {33}}}}\end{aligned}}

Чтобы получить курносый куб с единичной длиной ребра, разделите все координаты выше на значение α, указанное выше.

Ортогональные проекции [ править ]

Курносый куб не имеет точечной симметрии , поэтому вершина спереди не соответствует противоположной вершине сзади.

Курносый куб имеет две специальные ортогональные проекции , по центру, по двум типам граней: треугольники, квадраты, и соответствуют А ₂ и В ₂ плоскостях кокстеровских .

Ортогональные проекции
В центре	Лицо треугольник	Face Square	Край
Твердый
Каркас
Проективная симметрия	[3]	[4] ⁺	[2]
Двойной

Сферическая мозаика [ править ]

Курносый куб также можно представить в виде сферической плитки и спроецировать на плоскость через стереографическую проекцию . Эта проекция является конформной , сохраняя углы, но не площади или длины. Дуги большого круга (геодезические) на сфере проецируются как дуги окружности на плоскость.

Ортографическая проекция	Стереографическая проекция
	квадрат -centered

Геометрические отношения [ править ]

Куб, ромбокубооктаэдр и курносый куб (анимированное расширение и скручивание )

Курносый куб можно создать, взяв шесть граней куба, потянув их наружу, чтобы они больше не соприкасались, а затем слегка повернуть их центры (все по часовой стрелке или все против часовой стрелки), пока не заполнятся промежутки между ними. с равносторонними треугольниками .

Равномерное чередование усеченного кубооктаэдра

Курносый куб также может быть получен из усеченного кубооктаэдра путем чередования . 24 вершины усеченного кубооктаэдра образуют многогранник, топологически эквивалентный курносому кубу; остальные 24 образуют его зеркальное отображение. В результате многогранник транзитивен по вершинам, но не однороден.

«Улучшенный» курносый куб с немного меньшей квадратной гранью и немного более крупными треугольными гранями по сравнению с однородным курносым кубом Архимеда полезен в качестве сферической конструкции . ^[2]

Связанные многогранники и мозаики [ править ]

Курносый куб - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдрические многогранники
Симметрия : [4,3], (* 432)							[4,3] ⁺ (432)	[1 ⁺ , 4,3] = [3,3] (* 332)		[3 ⁺ , 4] (3 * 2)
{4,3}	т {4,3}	г {4,3} г {3 ^1,1 }	т {3,4} т {3 ^1,1 }	{3,4} {3 ^1,1 }	rr {4,3} s ₂ {3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	ч 2 {4,3} т {3,3}	с {3,4} с {3 ^1,1 }

		знак равно	знак равно	знак равно				знак равно или же	знак равно или же	знак равно

Двойники к однородным многогранникам
V4 3	V3.8 2	В (3,4) 2	V4.6 2	V3 4	V3.4 3	V4.6.8	V3 4 .4	V3 3	V3.6 2	V3 5

Этот полуправильный многогранник является членом последовательности курносых многогранников и мозаик с вершинной фигурой (3.3.3.3. N ) и диаграммой Кокстера – Дынкина . Эти фигуры и их двойники имеют ( n 32) вращательную симметрию , находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любого большего n . Можно считать, что серия начинается с n = 2, причем один набор граней вырождается в двуугольники .

n 32 мутации симметрии курносых мозаик: 3.3.3.3.n v т е
Симметрия n 32	Сферический				Евклидово	Компактный гиперболический		Paracomp.
Симметрия n 32	232	332	432	532	632	732	832	∞32
Курносые фигуры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Фигуры гироскопа
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Курносый куб является вторым в серии курносых многогранников и паркетов с вершиной фигурой 3.3.4.3. п .

4 n 2 мутации симметрии курносых мозаик : 3.3.4.3.n v т е
Симметрия 4 n 2	Сферический		Евклидово	Компактный гиперболический				Paracomp.
Симметрия 4 n 2	242	342	442	542	642	742	842	∞42
Курносые фигуры
Конфиг.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Фигуры гироскопа
Конфиг.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Курносый кубический граф [ править ]

Курносый кубический граф
4-х кратная симметрия
Вершины	24
Края	60
Автоморфизмы	24
Характеристики	Гамильтониан , регулярный
Таблица графиков и параметров

В математической области теории графов , курносый кубические граф является графом вершин и ребер из курносой кубы , один из Архимеда твердых тел . Он имеет 24 вершины и 60 ребер и является архимедовым графом . ^[3]

Ортогональная проекция

См. Также [ править ]

Соединение двух курносых кубиков
Курносый додекаэдр
Плоская квадратная черепица
Усеченный куб

Ссылки [ править ]

^ "Курносый куб - Калькулятор геометрии" . rechneronline.de . Проверено 26 мая 2020 .
^ "Сферические конструкции" RH Hardin и NJA Sloane
^ Читать, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269

Джаятилаке, Удая (март 2005 г.). «Вычисления на правильных многогранниках с гранями и вершинами». Математический вестник . 89 (514): 76–81.
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X. (Раздел 3-9)
Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN 0-521-55432-2.

Внешние ссылки [ править ]

Эрик В. Вайсштейн , Snub cube ( архимедово твердое тело ) в MathWorld .
- Вайсштейн, Эрик У. «Плоский кубический граф» . MathWorld .
Клитцинг, Ричард. "3D выпуклые равномерные многогранники s3s4s - snic" .
Равномерные многогранники
Многогранники виртуальной реальности Энциклопедия многогранников
Редактируемая сетка для печати Snub Cube с интерактивным 3D-видом

[1] "Курносый куб - Калькулятор геометрии" . rechneronline.de . Проверено 26 мая 2020 .

[2] "Сферические конструкции" RH Hardin и NJA Sloane

[3] Читать, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269