Навигация по большому кругу

Ортодромный курс нарисован на земном шаре.

Большой круг навигация или ортодромная навигация (связанная с ортодромном конечно , от греческого ορθóς , под прямым угла, и δρóμος , путь) является практикой навигации судна (а корабль или самолет ) вдоль большого круга . Такие маршруты обеспечивают кратчайшее расстояние между двумя точками земного шара. ^[1]

Курс [ править ]

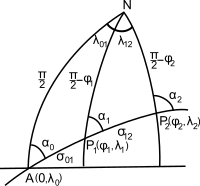
Рис. 1. Путь по большому кругу между (φ ₁ , λ ₁ ) и (φ ₂ , λ ₂ ).

Путь большого круга может быть найден с помощью сферической тригонометрии ; это сферический вариант обратной геодезической задачи . Если навигатор начинает с точки P ₁ = (φ ₁ , λ ₁ ) и планирует проехать по большому кругу до точки в точке P ₂ = (φ ₂ , λ ₂ ) (см. Рис. 1, φ - широта, положительная на север). , λ - долгота, положительная на восток), начальный и конечный курсы α ₁ и α ₂ задаются формулами для решения сферического треугольника

{\ displaystyle {\ begin {align} \ tan \ alpha _ {1} & = {\ frac {\ cos \ phi _ {2} \ sin \ lambda _ {12}} {\ cos \ phi _ {1} \ sin \ phi _ {2} - \ sin \ phi _ {1} \ cos \ phi _ {2} \ cos \ lambda _ {12}}}, \\\ tan \ alpha _ {2} & = {\ frac {\ cos \ phi _ {1} \ sin \ lambda _ {12}} {- \ cos \ phi _ {2} \ sin \ phi _ {1} + \ sin \ phi _ {2} \ cos \ phi _ {1} \ cos \ lambda _ {12}}}, \\\ конец {выровнено}}}

где λ ₁₂ = λ ₂ - λ ₁^{[примечание 1],} а квадранты α ₁ , α ₂ определяются знаками числителя и знаменателя в формулах касательных (например, с использованием функции atan2 ). Центральный угол между двумя точками, σ ₁₂ , задается

\tan \sigma _{12}={\frac {\sqrt {(\cos \phi _{1}\sin \phi _{2}-\sin \phi _{1}\cos \phi _{2}\cos \lambda _{12})^{2}+(\cos \phi _{2}\sin \lambda _{12})^{2}}}{\sin \phi _{1}\sin \phi _{2}+\cos \phi _{1}\cos \phi _{2}\cos \lambda _{12}}}.

^{[примечание 2]}^{[примечание 3]}

(Числитель этой формулы содержит величины, которые использовались для определения tanα _1. ) Тогда расстояние по большому кругу будет s ₁₂ = R σ ₁₂ , где R - предполагаемый радиус Земли, а σ ₁₂ выражается в радианах. . Используя средний радиус Земли , R = R ₁ ≈ 6 371 км (3 959 миль) дает результаты для расстояния s _12, которые находятся в пределах 1% геодезического расстояния для эллипсоида WGS84 .

Поиск путевых точек [ править ]

Чтобы найти путевые точки , то есть положения выбранных точек на большом круге между точками P ₁ и P ₂ , мы сначала экстраполируем большой круг обратно в его узел A , точку, в которой большой круг пересекает экватор на севере. направление: пусть долгота этой точки будет λ ₀ - см. рис. 1. Азимут в этой точке α ₀ определяется как

\tan \alpha _{0}={\frac {\sin \alpha _{1}\cos \phi _{1}}{\sqrt {\cos ^{2}\alpha _{1}+\sin ^{2}\alpha _{1}\sin ^{2}\phi _{1}}}}.

^{[примечание 4]}

Пусть угловые расстояния вдоль большого круга от A до P ₁ и P ₂ равны σ ₀₁ и σ ₀₂ соответственно. Тогда, используя правила Напьера, мы имеем

\tan \sigma _{01}={\frac {\tan \phi _{1}}{\cos \alpha _{1}}}\qquad

(Если φ ₁ = 0 и α ₁ = ¹ / ₂ я, использование σ ₀₁ = 0).

Это дает σ ₀₁ , откуда σ ₀₂ = σ ₀₁ + σ ₁₂ .

Долгота в узле находится из

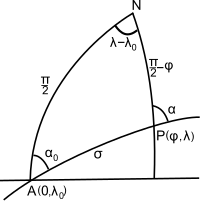
{\begin{aligned}\tan \lambda _{01}&={\frac {\sin \alpha _{0}\sin \sigma _{01}}{\cos \sigma _{01}}},\\\lambda _{0}&=\lambda _{1}-\lambda _{01}.\end{aligned}}

Рис. 2. Путь по дуге большого круга между узлом (пересечение экватора) и произвольной точкой (φ, λ).

Наконец, вычислите положение и азимут в произвольной точке P (см. Рис. 2) с помощью сферической версии прямой геодезической задачи . ^{[примечание 5]} Правила Нэпьера дают

{\color {white}.\,\qquad )}\tan \phi ={\frac {\cos \alpha _{0}\sin \sigma }{\sqrt {\cos ^{2}\sigma +\sin ^{2}\alpha _{0}\sin ^{2}\sigma }}},

^{[примечание 6]}

{\begin{aligned}\tan(\lambda -\lambda _{0})&={\frac {\sin \alpha _{0}\sin \sigma }{\cos \sigma }},\\\tan \alpha &={\frac {\tan \alpha _{0}}{\cos \sigma }}.\end{aligned}}

Atan2 функция должна быть использована для определения сг ₀₁ , X и а. Например, чтобы найти середину пути, замена σ = ¹ / ₂ (σ ₀₁ + σ ₀₂ ); в качестве альтернативы , чтобы найти точку на расстоянии D от начальной точки, принять σ = σ ₀₁ + d / R . Аналогично, вершина , точка на большом круге с наибольшей широтой, определяется путем подстановки σ = + ¹ / ₂ я. Может быть удобно параметризовать маршрут с точки зрения долготы, используя

\tan \phi =\cot \alpha _{0}\sin(\lambda -\lambda _{0}).

^{[примечание 7]}

Широты через равные интервалы долготы могут быть найдены, а полученные положения перенесены на карту Меркатора, что позволяет аппроксимировать большой круг серией линий румба . Определенный таким образом путь дает большой эллипс, соединяющий конечные точки, при условии, что координаты интерпретируются как географические координаты на эллипсоиде. $(\phi ,\lambda )$

Эти формулы применимы к сферической модели Земли. Они также используются для определения большого круга на вспомогательной сфере, которая является устройством для нахождения кратчайшего пути или геодезической на эллипсоиде вращения; см. статью о геодезических на эллипсоиде .

Пример [ править ]

Вычислите маршрут большого круга от Вальпараисо , φ ₁ = −33 °, λ ₁ = −71,6 °, до Шанхая , φ ₂ = 31,4 °, λ ₂ = 121,8 °.

Формулы для курса и расстояния дают λ ₁₂ = −166,6 °, ^{[примечание 8]} α ₁ = −94,41 °, α ₂ = −78,42 ° и σ ₁₂ = 168,56 °. Если принять радиус Земли R = 6371 км, то получим s ₁₂ = 18743 км.

Чтобы вычислить точки вдоль маршрута, сначала найдите α ₀ = −56,74 °, σ ₁ = −96,76 °, σ ₂ = 71,8 °, λ ₀₁ = 98,07 ° и λ ₀ = −169,67 °. Затем , чтобы вычислить среднюю точку маршрута (например), принять σ = ¹ / ₂ (σ ₁ + σ ₂ ) = -12,48 °, и решить для φ = -6,81 °, λ = -159,18 ° и α = -57,36 °.

Если геодезическая вычислена точно на эллипсоиде WGS84 , ^[4] результаты будут α ₁ = −94,82 °, α ₂ = −78,29 ° и s ₁₂ = 18752 км. Середина геодезической равна φ = −7,07 °, λ = −159,31 °, α = −57,45 °.

Гномоническая карта [ править ]

Прямая линия, проведенная на гномонической карте, была бы траекторией большого круга. Когда это переносится на диаграмму Меркатора , она становится кривой. Позиции переносятся с удобным интервалом долготы, и это отображается на карте Меркатора.

См. Также [ править ]

Картушка
Большой круг
Расстояние по большому кругу
Большой эллипс
Геодезические на эллипсоиде
Географическое расстояние
Изоазимутал
Локсодромная навигация
карта
- Карта Портолана
Морские песочные часы
Линия румба
Сферическая тригонометрия
Сеть Роза ветров

Заметки [ править ]

^ В статье о расстояниях большого круга используются обозначения Δλ = λ₁₂ и Δσ = σ₁₂ . Обозначения в этой статье необходимы, чтобы иметь дело с различиями между другими точками, например, λ₀₁ .
^ Более простая формула
$\cos \sigma _{12}=\sin \phi _{1}\sin \phi _{2}+\cos \phi _{1}\cos \phi _{2}\cos \lambda _{12};$
однако это менее точно, если σ ₁₂ мало.
^ Эти уравнения для α₁ , α₂ , σ₁₂ подходят для реализации на современных калькуляторах и компьютерах. Для ручных вычислений с логарифмами обычно использовалисьаналогии Деламбра ^[2] :
${\begin{aligned}\cos {\tfrac {1}{2}}(\alpha _{2}+\alpha _{1})\sin {\tfrac {1}{2}}\sigma _{12}&=\sin {\tfrac {1}{2}}(\phi _{2}-\phi _{1})\cos {\tfrac {1}{2}}\lambda _{12},\\\sin {\tfrac {1}{2}}(\alpha _{2}+\alpha _{1})\sin {\tfrac {1}{2}}\sigma _{12}&=\cos {\tfrac {1}{2}}(\phi _{2}+\phi _{1})\sin {\tfrac {1}{2}}\lambda _{12},\\\cos {\tfrac {1}{2}}(\alpha _{2}-\alpha _{1})\cos {\tfrac {1}{2}}\sigma _{12}&=\cos {\tfrac {1}{2}}(\phi _{2}-\phi _{1})\cos {\tfrac {1}{2}}\lambda _{12},\\\sin {\tfrac {1}{2}}(\alpha _{2}-\alpha _{1})\cos {\tfrac {1}{2}}\sigma _{12}&=\sin {\tfrac {1}{2}}(\phi _{2}+\phi _{1})\sin {\tfrac {1}{2}}\lambda _{12}.\end{aligned}}$
Маккоу ^[3] называет эти уравнения «логарифмической формой», имея в виду, что все тригонометрические термины появляются как произведения; это минимизирует количество требуемых поисков в таблице. Кроме того, избыточность этих формул служит для проверки расчетов. При использовании этих уравнений для определения более короткого пути на большом круге необходимо обеспечить, чтобы | λ ₁₂ | ≤ π (иначе будет найден более длинный путь).
^ Более простая формула
$\sin \alpha _{0}=\sin \alpha _{1}\cos \phi _{1};$
однако, это является менее точным , α ₀ ≈ ± ¹ / ₂ π.
^ Прямая геодезическая задача, нахождение положения P _{2 с} учетом P ₁ , α₁ и s ₁₂ , также может быть решена с помощью формул для решения сферического треугольника следующим образом:
${\begin{aligned}\sigma _{12}&=s_{12}/R,\\\sin \phi _{2}&=\sin \phi _{1}\cos \sigma _{12}+\cos \phi _{1}\sin \sigma _{12}\cos \alpha _{1},\quad {\text{or}}\\\tan \phi _{2}&={\frac {\sin \phi _{1}\cos \sigma _{12}+\cos \phi _{1}\sin \sigma _{12}\cos \alpha _{1}}{\sqrt {(\cos \phi _{1}\cos \sigma _{12}-\sin \phi _{1}\sin \sigma _{12}\cos \alpha _{1})^{2}+(\sin \sigma _{12}\sin \alpha _{1})^{2}}}},\\\tan \lambda _{12}&={\frac {\sin \sigma _{12}\sin \alpha _{1}}{\cos \phi _{1}\cos \sigma _{12}-\sin \phi _{1}\sin \sigma _{12}\cos \alpha _{1}}},\\\lambda _{2}&=\lambda _{1}+\lambda _{12},\\\tan \alpha _{2}&={\frac {\sin \alpha _{1}}{\cos \sigma _{12}\cos \alpha _{1}-\tan \phi _{1}\sin \sigma _{12}}}.\end{aligned}}$
Решение для путевых точек, приведенное в основном тексте, является более общим, чем это решение, поскольку оно позволяет находить путевые точки на заданных долготах. Кроме того, решение для σ (то есть положение узла) необходимо при нахождении геодезических на эллипсоиде с помощью вспомогательной сферы.
^ Более простая формула
$\sin \phi =\cos \alpha _{0}\sin \sigma ;$
однако, это является менее точным , когда φ ≈ ± ¹ / ₂ π
^ Используется следующее: $\cos \sigma =\cos \phi \cos(\lambda -\lambda _{0})$
^ λ₁₂ сокращается до диапазона [-180 °, 180 °] путем добавления или вычитания 360 ° по мере необходимости.

Ссылки [ править ]

^ Адам Вайнтрит; Томаш Нойман (7 июня 2011 г.). Методы и алгоритмы судоходства: морское судоходство и безопасность морских перевозок . CRC Press . С. 139–. ISBN 978-0-415-69114-7.
^ Тодхантер, И. (1871). Сферическая тригонометрия (3-е изд.). Макмиллан. п. 26 .
Перейти ↑ McCaw, GT (1932). «Длинные линии на Земле». Обзор обзора империи . 1 (6): 259–263. DOI : 10,1179 / sre.1932.1.6.259 .
^ Карни, CFF (2013). «Алгоритмы геодезических» . J. Geodesy . 87 (1): 43–55. DOI : 10.1007 / s00190-012-0578-Z .

Внешние ссылки [ править ]

Великий круг - из описания Великого круга MathWorld , фигур и уравнений. Mathworld, Wolfram Research, Inc. c1999 г.
Great Circle Mapper Интерактивный инструмент для построения маршрутов по большому кругу.
Калькулятор Большого Круга, рассчитывающий (начальный) курс и расстояние между двумя точками.
Great Circle Distance Графический инструмент для рисования больших кругов на картах. Также показывает расстояние и азимут в таблице.
Программа помощи Google для ортодромной навигации

[2] В статье о расстояниях большого круга используются обозначения Δλ = λ₁₂ и Δσ = σ₁₂ . Обозначения в этой статье необходимы, чтобы иметь дело с различиями между другими точками, например, λ₀₁ .

[3] Более простая формула
$\cos \sigma _{12}=\sin \phi _{1}\sin \phi _{2}+\cos \phi _{1}\cos \phi _{2}\cos \lambda _{12};$
однако это менее точно, если σ ₁₂ мало.

[6] Эти уравнения для α₁ , α₂ , σ₁₂ подходят для реализации на современных калькуляторах и компьютерах. Для ручных вычислений с логарифмами обычно использовалисьаналогии Деламбра ^[2] :
${\begin{aligned}\cos {\tfrac {1}{2}}(\alpha _{2}+\alpha _{1})\sin {\tfrac {1}{2}}\sigma _{12}&=\sin {\tfrac {1}{2}}(\phi _{2}-\phi _{1})\cos {\tfrac {1}{2}}\lambda _{12},\\\sin {\tfrac {1}{2}}(\alpha _{2}+\alpha _{1})\sin {\tfrac {1}{2}}\sigma _{12}&=\cos {\tfrac {1}{2}}(\phi _{2}+\phi _{1})\sin {\tfrac {1}{2}}\lambda _{12},\\\cos {\tfrac {1}{2}}(\alpha _{2}-\alpha _{1})\cos {\tfrac {1}{2}}\sigma _{12}&=\cos {\tfrac {1}{2}}(\phi _{2}-\phi _{1})\cos {\tfrac {1}{2}}\lambda _{12},\\\sin {\tfrac {1}{2}}(\alpha _{2}-\alpha _{1})\cos {\tfrac {1}{2}}\sigma _{12}&=\sin {\tfrac {1}{2}}(\phi _{2}+\phi _{1})\sin {\tfrac {1}{2}}\lambda _{12}.\end{aligned}}$
Маккоу ^[3] называет эти уравнения «логарифмической формой», имея в виду, что все тригонометрические термины появляются как произведения; это минимизирует количество требуемых поисков в таблице. Кроме того, избыточность этих формул служит для проверки расчетов. При использовании этих уравнений для определения более короткого пути на большом круге необходимо обеспечить, чтобы | λ ₁₂ | ≤ π (иначе будет найден более длинный путь).

[7] Более простая формула
$\sin \alpha _{0}=\sin \alpha _{1}\cos \phi _{1};$
однако, это является менее точным , α ₀ ≈ ± ¹ / ₂ π.

[8] Прямая геодезическая задача, нахождение положения P _{2 с} учетом P ₁ , α₁ и s ₁₂ , также может быть решена с помощью формул для решения сферического треугольника следующим образом:
${\begin{aligned}\sigma _{12}&=s_{12}/R,\\\sin \phi _{2}&=\sin \phi _{1}\cos \sigma _{12}+\cos \phi _{1}\sin \sigma _{12}\cos \alpha _{1},\quad {\text{or}}\\\tan \phi _{2}&={\frac {\sin \phi _{1}\cos \sigma _{12}+\cos \phi _{1}\sin \sigma _{12}\cos \alpha _{1}}{\sqrt {(\cos \phi _{1}\cos \sigma _{12}-\sin \phi _{1}\sin \sigma _{12}\cos \alpha _{1})^{2}+(\sin \sigma _{12}\sin \alpha _{1})^{2}}}},\\\tan \lambda _{12}&={\frac {\sin \sigma _{12}\sin \alpha _{1}}{\cos \phi _{1}\cos \sigma _{12}-\sin \phi _{1}\sin \sigma _{12}\cos \alpha _{1}}},\\\lambda _{2}&=\lambda _{1}+\lambda _{12},\\\tan \alpha _{2}&={\frac {\sin \alpha _{1}}{\cos \sigma _{12}\cos \alpha _{1}-\tan \phi _{1}\sin \sigma _{12}}}.\end{aligned}}$
Решение для путевых точек, приведенное в основном тексте, является более общим, чем это решение, поскольку оно позволяет находить путевые точки на заданных долготах. Кроме того, решение для σ (то есть положение узла) необходимо при нахождении геодезических на эллипсоиде с помощью вспомогательной сферы.

[9] Более простая формула
$\sin \phi =\cos \alpha _{0}\sin \sigma ;$
однако, это является менее точным , когда φ ≈ ± ¹ / ₂ π

[10] Используется следующее: $\cos \sigma =\cos \phi \cos(\lambda -\lambda _{0})$

[11] λ₁₂ сокращается до диапазона [-180 °, 180 °] путем добавления или вычитания 360 ° по мере необходимости.

[WeintritNeumann2011-1] Адам Вайнтрит; Томаш Нойман (7 июня 2011 г.). Методы и алгоритмы судоходства: морское судоходство и безопасность морских перевозок . CRC Press . С. 139–. ISBN 978-0-415-69114-7.

[4] Тодхантер, И. (1871). Сферическая тригонометрия (3-е изд.). Макмиллан. п. 26 .

[5] Перейти ↑ McCaw, GT (1932). «Длинные линии на Земле». Обзор обзора империи . 1 (6): 259–263. DOI : 10,1179 / sre.1932.1.6.259 .

[12] Карни, CFF (2013). «Алгоритмы геодезических» . J. Geodesy . 87 (1): 43–55. DOI : 10.1007 / s00190-012-0578-Z .

[1]