Логнормальное распределение

Лог-нормальный

Функция плотности вероятности 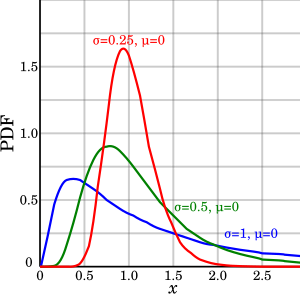Идентичный параметр, но разные параметры${\ displaystyle \ mu}$${\ displaystyle \ sigma}$
Кумулятивная функция распределения ${\ displaystyle \ mu = 0}$
Обозначение	${\displaystyle \operatorname {Lognormal} (\mu ,\,\sigma ^{2})}$
Параметры	${\displaystyle \mu \in (-\infty ,+\infty )}$, ${\displaystyle \sigma >0}$
Поддерживать	${\displaystyle x\in (0,+\infty )}$
PDF	${\displaystyle {\frac {1}{x\sigma {\sqrt {2\pi }}}}\ \exp \left({\text{-}}{\frac {\left(\ln x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$
CDF	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\Big [}{\frac {\ln x-\mu }{{\sqrt {2}}\sigma }}{\Big ]}}$
Квантиль	${\displaystyle \exp(\mu +{\sqrt {2\sigma ^{2}}}\operatorname {erf} ^{-1}(2p-1))}$
Иметь в виду	${\displaystyle \exp \left(\mu +{\frac {\sigma ^{2}}{2}}\right)}$
Медиана	${\displaystyle \exp(\mu )}$
Режим	${\displaystyle \exp(\mu -\sigma ^{2})}$
Дисперсия	${\displaystyle [\exp(\sigma ^{2})-1]\exp(2\mu +\sigma ^{2})}$
Асимметрия	${\displaystyle (\exp(\sigma ^{2})+2){\sqrt {\exp(\sigma ^{2})-1}}}$
Бывший. эксцесс	${\displaystyle \exp(4\sigma ^{2})+2\exp(3\sigma ^{2})+3\exp(2\sigma ^{2})-6}$
Энтропия	${\displaystyle \log _{2}(\sigma e^{\mu +{\tfrac {1}{2}}}{\sqrt {2\pi }})}$
MGF	определяется только для чисел с неположительной действительной частью, см. текст
CF	представление асимптотически расходится, но достаточно для численных целей${\displaystyle \sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}}$
Информация Fisher	${\displaystyle {\begin{pmatrix}1/\sigma ^{2}&0\\0&1/2\sigma ^{2}\end{pmatrix}}}$
Метод моментов	${\displaystyle \mu =\log \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {Var} [X]+\operatorname {E} [X]^{2}}}}\right)}$, ${\displaystyle \sigma ^{2}=\log \left({\frac {\operatorname {Var} [X]}{\operatorname {E} [X]^{2}}}+1\right)}$

В теории вероятностей , А распределение логнормальный (или логнормальный) является непрерывным распределением вероятностей из случайной величины которой логарифм является нормально распределенным . Таким образом, если случайная величина X имеет логнормальное распределение, то Y = ln ( X ) имеет нормальное распределение. ^{[1] [2] [3]} Эквивалентно, если У имеет нормальное распределение, то в экспоненциальной функции из Y , Х = ехр ( Y ), имеет логнормальное распределение. Случайная величина, которая имеет логарифмическое нормальное распределение, принимает только положительные действительные значения. Это удобная и полезная модель для измерений в точных и технических науках, а также в медицине , экономике и других областях (например, энергии, концентрации, длины, финансовой отдачи и других показателей).

Это распределение иногда называют распределением Гальтона или распределением Гальтона в честь Фрэнсиса Гальтона . ^[4] Логнормальное распределение также было связано с другими именами, такими как Макалистер, Гибрат и Кобб-Дуглас . ^[4]

Логнормальный процесс - это статистическая реализация мультипликативного произведения многих независимых случайных величин , каждая из которых положительна. Это оправдывается рассмотрением центральной предельной теоремы в лог-области (иногда называемой законом Гибрата ). Логнормальное распределение - это максимальное распределение вероятностей энтропии для случайной переменной X, для которой указаны среднее значение и дисперсия ln ( X ) . ^[5]

Определения [ править ]

Генерация и параметры [ править ]

Позвольте быть стандартной нормальной переменной , и позвольте и быть двумя действительными числами. Тогда распределение случайной величины ${\displaystyle Z}$${\displaystyle \mu }$${\displaystyle \sigma >0}$

${\displaystyle X=e^{\mu +\sigma Z}}$

называется логнормальным распределением с параметрами и . Это ожидаемое значение (или среднее значение ) и стандартное отклонение натурального логарифма переменной , а не само математическое ожидание и стандартное отклонение .${\displaystyle \mu }$${\displaystyle \sigma }$${\displaystyle X}$

Связь между нормальным и логнормальным распределением. Если нормально распределяется, то логарифмически нормально распределяется.${\displaystyle Y=\mu +\sigma Z}$${\displaystyle X\sim e^{Y}}$

Это соотношение верно независимо от основания логарифмической или экспоненциальной функции: если оно нормально распределено, то то же самое и для любых двух положительных чисел . Точно так же, если логарифм нормально распределен, то так и есть , где .${\displaystyle \log _{a}(X)}$${\displaystyle \log _{b}(X)}$${\displaystyle a,b\neq 1}$${\displaystyle e^{Y}}$${\displaystyle a^{Y}}$${\displaystyle 0<a\neq 1}$

Чтобы получить распределение с желаемым средним значением и дисперсией , используются и ${\displaystyle \mu _{X}}$${\displaystyle \sigma _{X}^{2}}$${\displaystyle \mu =\ln \left({\frac {\mu _{X}^{2}}{\sqrt {\mu _{X}^{2}+\sigma _{X}^{2}}}}\right)}$${\displaystyle \sigma ^{2}=\ln \left(1+{\frac {\sigma _{X}^{2}}{\mu _{X}^{2}}}\right)}$

В качестве альтернативы можно использовать «мультипликативный» или «геометрический» параметры и . Они имеют более прямую интерпретацию: это медиана распределения, полезная для определения интервалов «разброса», см. Ниже.${\displaystyle \mu ^{*}=e^{\mu }}$${\displaystyle \sigma ^{*}=e^{\sigma }}$${\displaystyle \mu ^{*}}$${\displaystyle \sigma ^{*}}$

Функция плотности вероятности [ править ]

Положительная случайная величина X имеет нормальное логарифмическое распределение (т. Е. ^[1] ), если натуральный логарифм X нормально распределен со средним значением и дисперсией :${\displaystyle X\sim \operatorname {Lognormal} (\mu _{x},\sigma _{x}^{2})}$${\displaystyle \mu }$${\displaystyle \sigma ^{2}}$

${\displaystyle \ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$

Пусть и - соответственно кумулятивная функция распределения вероятностей и функция плотности вероятности распределения N (0,1), тогда мы имеем, что ^{[2] [4]}${\displaystyle \Phi }$${\displaystyle \varphi }$

${\displaystyle {\begin{aligned}f_{X}(x)&={\frac {\rm {d}}{{\rm {d}}x}}\Pr(X\leq x)={\frac {\rm {d}}{{\rm {d}}x}}\Pr(\ln X\leq \ln x)={\frac {\rm {d}}{{\rm {d}}x}}\Phi \left({\frac {\ln x-\mu }{\sigma }}\right)\\[6pt]&=\varphi \left({\frac {\ln x-\mu }{\sigma }}\right){\frac {\rm {d}}{{\rm {d}}x}}\left({\frac {\ln x-\mu }{\sigma }}\right)=\varphi \left({\frac {\ln x-\mu }{\sigma }}\right){\frac {1}{\sigma x}}\\[6pt]&={\frac {1}{x\sigma {\sqrt {2\pi \,}}}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right).\end{aligned}}}$

Кумулятивная функция распределения [ править ]

Кумулятивная функция распределения является

${\displaystyle F_{X}(x)=\Phi \left({\frac {(\ln x)-\mu }{\sigma }}\right)}$

где - кумулятивная функция распределения стандартного нормального распределения (т. е. N (0,1)).${\displaystyle \Phi }$

Это также может быть выражено следующим образом: ^[2]

${\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)}$

где erfc - дополнительная функция ошибок .

Многомерный нормальный логарифм [ править ]

Если - многомерное нормальное распределение , то имеет многомерное логнормальное распределение ^{[6] [7]} со средним${\displaystyle {\boldsymbol {X}}\sim {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})}$${\displaystyle {\boldsymbol {Y}}=\exp({\boldsymbol {X}})}$

${\displaystyle \operatorname {E} [{\boldsymbol {Y}}]_{i}=e^{\mu _{i}+{\frac {1}{2}}\Sigma _{ii}},}$

и ковариационная матрица

${\displaystyle \operatorname {Var} [{\boldsymbol {Y}}]_{ij}=e^{\mu _{i}+\mu _{j}+{\frac {1}{2}}(\Sigma _{ii}+\Sigma _{jj})}(e^{\Sigma _{ij}}-1).}$

Поскольку многомерное логнормальное распределение широко не используется, остальная часть этой статьи имеет дело только с одномерным распределением .

Характеристическая функция и функция создания момента [ править ]

Все моменты логнормального распределения существуют и

${\displaystyle \operatorname {E} [X^{n}]=e^{n\mu +n^{2}\sigma ^{2}/2}}$

Это можно получить, допуская интеграл. Однако логнормальное распределение не определяется его моментами. ^[8] Это означает, что он не может иметь определенной производящей функции момента в окрестности нуля. ^[9] Действительно, ожидаемое значение не определено для любого положительного значения аргумента , поскольку определяющий интеграл расходится.${\displaystyle z={\tfrac {\ln(x)-(\mu +n\sigma ^{2})}{\sigma }}}$${\displaystyle \operatorname {E} [e^{tX}]}$${\displaystyle t}$

Характеристическая функция определена для действительных значений т , но не определена для любого комплексного значения т , который имеет отрицательную мнимую часть, и , следовательно , функция характерна не аналитическая в начале координат. Следовательно, характеристическая функция логнормального распределения не может быть представлена ​​в виде бесконечного сходящегося ряда. ^[10] В частности, его формальный ряд Тейлора расходится:${\displaystyle \operatorname {E} [e^{itX}]}$

${\displaystyle \sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}}$

Однако был получен ряд альтернативных представлений расходящихся рядов . ^{[10] [11] [12] [13]}

Формула в замкнутом виде для характеристической функции с в области сходимости неизвестна. Относительно простая аппроксимирующая формула доступна в закрытом виде и приведена в ^[14]${\displaystyle \varphi (t)}$${\displaystyle t}$

${\displaystyle \varphi (t)\approx {\frac {\exp \left(-{\frac {W^{2}(-it\sigma ^{2}e^{\mu })+2W(-it\sigma ^{2}e^{\mu })}{2\sigma ^{2}}}\right)}{\sqrt {1+W(-it\sigma ^{2}e^{\mu })}}}}$

где - W-функция Ламберта . Это приближение получается асимптотическим методом, но оно остается точным во всей области сходимости .${\displaystyle W}$${\displaystyle \varphi }$

Свойства [ править ]

Геометрические или мультипликативные моменты [ править ]

Геометрическое или мультипликативный среднее логарифмически нормального распределения . Он равен медиане. Геометрическая или мультипликативный стандартное отклонение это . ^{[15] [16]}${\displaystyle \operatorname {GM} [X]=e^{\mu }=\mu ^{*}}$${\displaystyle \operatorname {GSD} [X]=e^{\sigma }=\sigma ^{*}}$

По аналогии с арифметической статистикой, можно определить геометрическую дисперсию, , и геометрический коэффициент вариации , ^[15] , было предложено. Этот термин был задуман как аналог коэффициента вариации для описания мультипликативной вариации в логарифмически нормальных данных, но это определение GCV не имеет теоретической основы в качестве самооценки (см. Также Коэффициент вариации ).${\displaystyle \operatorname {GVar} [X]=e^{\sigma ^{2}}}$ ${\displaystyle \operatorname {GCV} [X]=e^{\sigma }-1}$${\displaystyle \operatorname {CV} }$

Обратите внимание, что среднее геометрическое меньше среднего арифметического. Это связано с неравенством AM – GM и соответствует выпуклому вниз логарифму. Фактически,

${\displaystyle \operatorname {E} [X]=e^{\mu +{\frac {1}{2}}\sigma ^{2}}=e^{\mu }\cdot {\sqrt {e^{\sigma ^{2}}}}=\operatorname {GM} [X]\cdot {\sqrt {\operatorname {GVar} [X]}}.}$^[17]

В финансах этот термин иногда интерпретируется как поправка на выпуклость . С точки зрения стохастического исчисления , это тот же поправочный член, что и в лемме Ито для геометрического броуновского движения .${\displaystyle e^{-{\frac {1}{2}}\sigma ^{2}}}$

Арифметические моменты [ править ]

Для любого действительного или комплексного числа п , то п -й момент из лог-нормально распределенной переменной X задается ^[4]

${\displaystyle \operatorname {E} [X^{n}]=e^{n\mu +{\frac {1}{2}}n^{2}\sigma ^{2}}.}$

В частности, среднее арифметическое, ожидаемое квадратическое значение, арифметическая дисперсия и стандартное арифметическое отклонение переменной X с нормальным логарифмическим распределением соответственно задаются следующим образом: ^[2]

${\displaystyle {\begin{aligned}\operatorname {E} [X]&=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}},\\[4pt]\operatorname {E} [X^{2}]&=e^{2\mu +2\sigma ^{2}},\\[4pt]\operatorname {Var} [X]&=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=(\operatorname {E} [X])^{2}(e^{\sigma ^{2}}-1)=e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1),\\[4pt]\operatorname {SD} [X]&={\sqrt {\operatorname {Var} [X]}}=\operatorname {E} [X]{\sqrt {e^{\sigma ^{2}}-1}}=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}}{\sqrt {e^{\sigma ^{2}}-1}},\end{aligned}}}$

Арифметический коэффициент вариации - это отношение . Для логнормального распределения он равен ^[3]${\displaystyle \operatorname {CV} [X]}$${\displaystyle {\tfrac {\operatorname {SD} [X]}{\operatorname {E} [X]}}}$

${\displaystyle \operatorname {CV} [X]={\sqrt {e^{\sigma ^{2}}-1}}.}$

Эту оценку иногда называют «геометрической CV» (GCV) ^{[18] [19]} из-за использования геометрической дисперсии. В отличие от стандартного арифметического отклонения, арифметический коэффициент вариации не зависит от среднего арифметического.

Параметры μ и σ могут быть получены, если известны среднее арифметическое и дисперсия:

${\displaystyle {\begin{aligned}\mu &=\ln \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {E} [X^{2}]}}}\right)=\ln \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {Var} [X]+\operatorname {E} [X]^{2}}}}\right),\\[4pt]\sigma ^{2}&=\ln \left({\frac {\operatorname {E} [X^{2}]}{\operatorname {E} [X]^{2}}}\right)=\ln \left(1+{\frac {\operatorname {Var} [X]}{\operatorname {E} [X]^{2}}}\right).\end{aligned}}}$

Распределение вероятностей не определяется однозначно моментами E [ X ⁿ ] = e ^{nμ +1/2n 2 σ 2} для n ≥ 1. То есть существуют другие распределения с таким же набором моментов. ^[4] Фактически, существует целое семейство распределений с теми же моментами, что и логнормальное распределение. ^{[ необходима цитата ]}

Режим, медиана, квантили [ править ]

Режим является точкой глобального максимума функции плотности вероятности. В частности, решая уравнение , мы получаем:${\displaystyle (\ln f)'=0}$

${\displaystyle \operatorname {Mode} [X]=e^{\mu -\sigma ^{2}}.}$

Поскольку лог-трансформированных переменная имеет нормальное распределение, и квантили сохраняются при монотонных преобразований, квантили являются ${\displaystyle Y=\ln X}$${\displaystyle X}$

${\displaystyle q_{X}(\alpha )=e^{\mu +\sigma q_{\Phi }(\alpha )}=\mu ^{*}(\sigma ^{*})^{q_{\Phi }(\alpha )},}$

где - квантиль стандартного нормального распределения.${\displaystyle q_{\Phi }(\alpha )}$

В частности, медиана логнормального распределения равна его мультипликативному среднему ^[20]

${\displaystyle \operatorname {Med} [X]=e^{\mu }=\mu ^{*}.}$

Частичное ожидание [ править ]

Частичное ожидание случайной величины относительно порога определяется как${\displaystyle X}$${\displaystyle k}$

${\displaystyle g(k)=\int _{k}^{\infty }xf_{X}(x)\,dx.}$

В качестве альтернативы, используя определение условного ожидания , его можно записать как . Для логнормальной случайной величины частичное ожидание определяется как:${\displaystyle g(k)=\operatorname {E} [X\mid X>k]P(X>k)}$

${\displaystyle g(k)=\int _{k}^{\infty }xf_{X}(x)\,dx=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}}\,\Phi \!\left({\frac {\mu +\sigma ^{2}-\ln k}{\sigma }}\right)}$

где - нормальная кумулятивная функция распределения . Вывод формулы представлен в обсуждении этой статьи в Википедии. ^{[ где? ]} Формула частичного математического ожидания имеет применения в страховании и экономике , она используется при решении уравнения в частных производных, приводящего к формуле Блэка – Шоулза .${\displaystyle \Phi }$

Условное ожидание [ править ]

Условное ожидание логнормальной случайной величины по отношению к порогу - это ее частичное ожидание, деленное на совокупную вероятность нахождения в этом диапазоне:${\displaystyle X}$${\displaystyle k}$

${\displaystyle {\begin{aligned}E[X\mid X<k]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\ln(k)-\mu -\sigma ^{2}}{\sigma }}\right]}{\Phi \left[{\frac {\ln(k)-\mu }{\sigma }}\right]}}\\[8pt]E[X\mid X\geqslant k]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\mu +\sigma ^{2}-\ln(k)}{\sigma }}\right]}{1-\Phi \left[{\frac {\ln(k)-\mu }{\sigma }}\right]}}\\[8pt]E[X\mid X\in [k_{1},k_{2}]]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\ln(k_{2})-\mu -\sigma ^{2}}{\sigma }}\right]-\Phi \left[{\frac {\ln(k_{1})-\mu -\sigma ^{2}}{\sigma }}\right]}{\Phi \left[{\frac {\ln(k_{2})-\mu }{\sigma }}\right]-\Phi \left[{\frac {\ln(k_{1})-\mu }{\sigma }}\right]}}\end{aligned}}}$

Альтернативные параметризации [ править ]

В дополнение к характеристике с помощью или существует несколько способов параметризации логнормального распределения. ProbOnto , база знаний и онтология вероятностных распределений ^{[21] [22],} перечисляет семь таких форм:${\displaystyle \mu ,\sigma }$${\displaystyle \mu ^{*},\sigma ^{*}}$

• LogNormal1 (μ, σ) со средним значением μ и стандартным отклонением σ, оба в логарифмической шкале ^[23]

  ${\displaystyle P(x;{\boldsymbol {\mu }},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left[{\frac {-(\log x-\mu )^{2}}{2\sigma ^{2}}}\right]}$

• LogNormal2 (μ, υ) со средним значением μ и дисперсией υ, оба в логарифмической шкале

  ${\displaystyle P(x;{\boldsymbol {\mu }},{\boldsymbol {v}})={\frac {1}{x{\sqrt {v}}{\sqrt {2\pi }}}}\exp \left[{\frac {-(\log x-\mu )^{2}}{2v}}\right]}$

• LogNormal3 (m, σ) с медианой m в натуральном масштабе и стандартным отклонением σ в логарифмической шкале ^[23]

  ${\displaystyle P(x;{\boldsymbol {m}},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left[{\frac {-[\log(x/m)]^{2}}{2\sigma ^{2}}}\right]}$

• LogNormal4 (m, cv) с медианой m и коэффициентом вариации cv, оба в натуральном масштабе

  ${\displaystyle P(x;{\boldsymbol {m}},{\boldsymbol {cv}})={\frac {1}{x{\sqrt {\log(cv^{2}+1)}}{\sqrt {2\pi }}}}\exp \left[{\frac {-[\log(x/m)]^{2}}{2\log(cv^{2}+1)}}\right]}$

• LogNormal5 (μ, τ) со средним значением μ и точностью τ в логарифмической шкале ^[24]

  ${\displaystyle P(x;{\boldsymbol {\mu }},{\boldsymbol {\tau }})={\sqrt {\frac {\tau }{2\pi }}}{\frac {1}{x}}\exp \left[{-{\frac {\tau }{2}}(\log x-\mu )^{2}}\right]}$

• LogNormal6 (m, σ _g ) со средним значением m и геометрическим стандартным отклонением σ _g , оба в натуральном масштабе ^[25]

  ${\displaystyle P(x;{\boldsymbol {m}},{\boldsymbol {\sigma _{g}}})={\frac {1}{x\log(\sigma _{g}){\sqrt {2\pi }}}}\exp \left[{\frac {-[\log(x/m)]^{2}}{2\log ^{2}(\sigma _{g})}}\right]}$

• LogNormal7 (μ _N , σ _N ) со средним значением μ _N и стандартным отклонением σ _N , оба в натуральном масштабе ^[26]

  ${\displaystyle P(x;{\boldsymbol {\mu _{N}}},{\boldsymbol {\sigma _{N}}})={\frac {1}{x{\sqrt {2\pi \log \left(1+\sigma _{N}^{2}/\mu _{N}^{2}\right)}}}}\exp \left({\frac {-{\Big [}\log(x)-\log {\Big (}{\frac {\mu _{N}}{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}}{\Big )}{\Big ]}^{2}}{2\log {\Big (}1+\sigma _{N}^{2}/\mu _{N}^{2}{\Big )}}}\right)}$

Примеры повторной параметризации [ править ]

Рассмотрим ситуацию, когда нужно запустить модель, используя два разных инструмента оптимального проектирования, например PFIM ^[27] и PopED. ^[28] Первый поддерживает LN2, второй - параметризацию LN7 соответственно. Следовательно, требуется повторная параметризация, иначе два инструмента дадут разные результаты.

Для перехода верны следующие формулы .${\displaystyle LN2(\mu ,v)\rightarrow LN7(\mu _{N},\sigma _{N})}$${\displaystyle \mu _{N}=\exp(\mu +v/2){\text{ and }}\sigma _{N}=\exp(\mu +v/2){\sqrt {\exp(v)-1}}}$

Для перехода верны следующие формулы .${\displaystyle LN7(\mu _{N},\sigma _{N})\rightarrow LN2(\mu ,v)}$${\displaystyle \mu =\log {\Big (}\mu _{N}/{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}{\Big )}{\text{ and }}v=\log(1+\sigma _{N}^{2}/\mu _{N}^{2})}$

Все остальные формулы повторной параметризации можно найти в документе спецификации на веб-сайте проекта. ^[29]

Множественное, Взаимное, Мощное [ править ]

• Умножение на константу: если тогда${\displaystyle X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle aX\sim \operatorname {Lognormal} (\mu +\ln a,\ \sigma ^{2}).}$
• Взаимный: Если то${\displaystyle X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle {\tfrac {1}{X}}\sim \operatorname {Lognormal} (-\mu ,\ \sigma ^{2}).}$
• Мощность: Если то для${\displaystyle X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle X^{a}\sim \operatorname {Lognormal} (a\mu ,\ a^{2}\sigma ^{2})}$${\displaystyle a\neq 0.}$

Умножение и деление независимых логнормальных случайных величин [ править ]

Если две независимые логарифмически нормальные переменные и умножаются [делятся], произведение [соотношение] снова логарифмически нормальное с параметрами [ ] и , где . Это легко обобщается на произведение таких переменных.${\displaystyle X_{1}}$${\displaystyle X_{2}}$${\displaystyle \mu =\mu _{1}+\mu _{2}}$${\displaystyle \mu =\mu _{1}-\mu _{2}}$${\displaystyle \sigma }$${\displaystyle \sigma ^{2}=\sigma _{1}^{2}+\sigma _{2}^{2}}$${\displaystyle n}$

В более общем смысле, если это независимые, логнормально распределенные переменные, то${\displaystyle X_{j}\sim \operatorname {Lognormal} (\mu _{j},\sigma _{j}^{2})}$${\displaystyle n}$${\displaystyle Y=\textstyle \prod _{j=1}^{n}X_{j}\sim \operatorname {Lognormal} {\Big (}\textstyle \sum _{j=1}^{n}\mu _{j},\ \sum _{j=1}^{n}\sigma _{j}^{2}{\Big )}.}$

Мультипликативная центральная предельная теорема [ править ]

Геометрическое или мультипликативное среднее независимых, одинаково распределенных положительных случайных величин показывает приблизительно логнормальное распределение с параметрами и , при условии, что оно конечно. ${\displaystyle n}$${\displaystyle X_{i}}$${\displaystyle n\to \infty }$${\displaystyle \mu =E[\ln(X_{i})]}$${\displaystyle \sigma ^{2}={\mbox{var}}[\ln(X_{i})]/n}$${\displaystyle \sigma ^{2}}$

Фактически, случайные величины не обязательно должны быть одинаково распределены. Достаточно, чтобы все распределения имели конечную дисперсию и удовлетворяли другим условиям любого из множества вариантов центральной предельной теоремы . ${\displaystyle \ln(X_{i})}$

Это широко известно как закон Гибрата .

Другое [ править ]

Набор данных, который возникает из логнормального распределения, имеет симметричную кривую Лоренца (см. Также коэффициент асимметрии Лоренца ). ^[30]

Гармонические , геометрические и арифметические средние этого распределения взаимосвязаны; ^[31] такое соотношение задается формулой${\displaystyle H}$${\displaystyle G}$${\displaystyle A}$

${\displaystyle H={\frac {G^{2}}{A}}.}$

Логарифмический нормальное распределение является бесконечно делимым , ^[32] , но они не являются устойчивыми распределениями , которые могут быть легко извлечь из. ^[33]

Связанные дистрибутивы [ править ]

• Если - нормальное распределение , то${\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$${\displaystyle \exp(X)\sim \operatorname {Lognormal} (\mu ,\sigma ^{2}).}$
• Если распределяется нормально логарифмически, то это нормальная случайная величина. ^[1]${\displaystyle X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle \ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$
• Пусть быть независимыми лог-нормально распределенных переменных , возможно , с изменением и параметров, а также . Распределение не имеет выражения в замкнутой форме, но может быть разумно аппроксимировано другим логнормальным распределением в правом хвосте. ^[34] Его функция плотности вероятности в окрестности 0 была охарактеризована ^[33], и она не похожа ни на какое логнормальное распределение. Обычно используемое приближение Л. Ф. Фентона (но ранее заявленное Р. И. Уилкинсоном и математическое обоснование Марлоу ^[35] ) получается путем сопоставления среднего и дисперсии другого логнормального распределения:${\displaystyle X_{j}\sim \operatorname {Lognormal} (\mu _{j},\sigma _{j}^{2})\ }$${\displaystyle \sigma }$${\displaystyle \mu }$${\displaystyle Y=\textstyle \sum _{j=1}^{n}X_{j}}$${\displaystyle Y}$${\displaystyle Z}$

${\displaystyle {\begin{aligned}\sigma _{Z}^{2}&=\ln \!\left[{\frac {\sum e^{2\mu _{j}+\sigma _{j}^{2}}(e^{\sigma _{j}^{2}}-1)}{(\sum e^{\mu _{j}+\sigma _{j}^{2}/2})^{2}}}+1\right],\\\mu _{Z}&=\ln \!\left[\sum e^{\mu _{j}+\sigma _{j}^{2}/2}\right]-{\frac {\sigma _{Z}^{2}}{2}}.\end{aligned}}}$

В случае, если у всех одинаковый параметр дисперсии , эти формулы упрощаются до${\displaystyle X_{j}}$${\displaystyle \sigma _{j}=\sigma }$

${\displaystyle {\begin{aligned}\sigma _{Z}^{2}&=\ln \!\left[(e^{\sigma ^{2}}-1){\frac {\sum e^{2\mu _{j}}}{(\sum e^{\mu _{j}})^{2}}}+1\right],\\\mu _{Z}&=\ln \!\left[\sum e^{\mu _{j}}\right]+{\frac {\sigma ^{2}}{2}}-{\frac {\sigma _{Z}^{2}}{2}}.\end{aligned}}}$

Для более точного приближения можно использовать метод Монте-Карло для оценки кумулятивной функции распределения, PDF и правого хвоста. ^{[36] [37]}

• Говорят, что If then имеет трехпараметрическое логарифмически нормальное распределение с поддержкой . ^[38] , .${\displaystyle X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle X+c}$${\displaystyle x\in (c,+\infty )}$ ${\displaystyle \operatorname {E} [X+c]=\operatorname {E} [X]+c}$${\displaystyle \operatorname {Var} [X+c]=\operatorname {Var} [X]}$
• Логнормальное распределение - это частный случай полуограниченного распределения Джонсона .
• Если с , то ( раздача Suzuki ).${\displaystyle X\mid Y\sim \operatorname {Rayleigh} (Y)\,}$${\displaystyle Y\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})}$${\displaystyle X\sim \operatorname {Suzuki} (\mu ,\sigma )}$
• Заменитель логнормального, интеграл которого может быть выражен через более элементарные функции ^[39], может быть получен на основе логистического распределения, чтобы получить приближение для CDF

${\displaystyle F(x;\mu ,\sigma )=\left[\left({\frac {e^{\mu }}{x}}\right)^{\pi /(\sigma {\sqrt {3}})}+1\right]^{-1}.}$

Это логистическое распределение .

Статистический вывод [ править ]

Оценка параметров [ править ]

Для определения оценок максимального правдоподобия параметров логнормального распределения μ и σ мы можем использовать ту же процедуру, что и для нормального распределения . Обратите внимание, что

${\displaystyle L(\mu ,\sigma )=\prod _{i=1}^{n}{\frac {1}{x_{i}}}\varphi _{\mu ,\sigma }(\ln x_{i})}$,

где - функция плотности нормального распределения . Следовательно, функция логарифмического правдоподобия${\displaystyle \varphi _{}}$${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$

${\displaystyle \ell (\mu ,\sigma \mid x_{1},x_{2},\ldots ,x_{n})=-\sum _{i}\ln x_{i}+\ell _{N}(\mu ,\sigma \mid \ln x_{1},\ln x_{2},\dots ,\ln x_{n})}$.

Поскольку первый член постоянен по отношению к μ и σ , обе логарифмические функции правдоподобия и достигают своего максимума с одинаковыми и . Следовательно, оценки максимального правдоподобия идентичны оценкам для нормального распределения наблюдений ,${\displaystyle \ell }$${\displaystyle \ell _{N}}$${\displaystyle \mu }$${\displaystyle \sigma }$${\displaystyle \ln x_{1},\ln x_{2},\dots ,\ln x_{n})}$

${\displaystyle {\widehat {\mu }}={\frac {\sum _{k}\ln x_{k}}{n}},\qquad {\widehat {\sigma }}^{2}={\frac {\sum _{k}\left(\ln x_{k}-{\widehat {\mu }}\right)^{2}}{n}}.}$

При конечном n эти оценки смещены. Хотя смещение для незначительно, менее смещенная оценка для нормального распределения получается заменой знаменателя n на n-1 в уравнении для .${\displaystyle {\widehat {\mu }}}$${\displaystyle \sigma }$${\displaystyle {\widehat {\sigma }}^{2}}$

Когда отдельные значения недоступны, но есть среднее по выборке и стандартное отклонение s , то соответствующие параметры определяются по следующим формулам, полученным в результате решения уравнений для математического ожидания и дисперсии для и :${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$${\displaystyle {\bar {x}}}$ ${\displaystyle \operatorname {E} [X]}$${\displaystyle \operatorname {Var} [X]}$${\displaystyle \mu }$${\displaystyle \sigma }$

${\displaystyle \mu =\ln \left({\bar {x}}\ {\Big /}\ {\sqrt {1+{\frac {{\widehat {\sigma }}^{2}}{{\bar {x}}^{2}}}}}\right),\qquad \sigma ^{2}=\ln \left(1+{\frac {{\widehat {\sigma }}^{2}}{{\bar {x}}^{2}}}\right)}$.

Статистика [ править ]

Наиболее эффективный способ анализа данных с нормальным логарифмическим распределением состоит в применении хорошо известных методов, основанных на нормальном распределении, к логарифмически преобразованным данным с последующим обратным преобразованием результатов, если это необходимо.

Интервалы разброса [ править ]

Базовый пример - интервалы разброса: для нормального распределения интервал содержит приблизительно две трети (68%) вероятности (или большой выборки) и содержит 95%. Следовательно, для логнормального распределения${\displaystyle [\mu -\sigma ,\mu +\sigma ]}$${\displaystyle [\mu -2\sigma ,\mu +2\sigma ]}$

${\displaystyle [\mu ^{*}/\sigma ^{*},\mu ^{*}\cdot \sigma ^{*}]=[\mu ^{*}{}^{\times }\!\!/\sigma ^{*}]}$ содержит 2/3, а

${\displaystyle [\mu ^{*}/(\sigma ^{*})^{2},\mu ^{*}\cdot (\sigma ^{*})^{2}]=[\mu ^{*}{}^{\times }\!\!/(\sigma ^{*})^{2}]}$ содержит 95%

вероятности. Используя оценочные параметры, в этих интервалах должно содержаться примерно одинаковое процентное соотношение данных.

Доверительный интервал для ${\displaystyle \mu ^{*}}$[ править ]

Используя этот принцип, обратите внимание, что доверительный интервал для is , где - стандартная ошибка, а q - 97,5% квантиль t-распределения с n-1 степенями свободы. Обратное преобразование приводит к доверительному интервалу для ,${\displaystyle \mu }$${\displaystyle [{\widehat {\mu }}\pm q\cdot {\widehat {\mathop {se} }}]}$${\displaystyle \mathop {se} ={\widehat {\sigma }}/{\sqrt {n}}}$${\displaystyle \mu ^{*}}$

${\displaystyle [{\widehat {\mu }}^{*}{}^{\times }\!\!/(\operatorname {sem} ^{*})^{q}]}$ с ${\displaystyle \operatorname {sem} ^{*}=({\widehat {\sigma }}^{*})^{1/{\sqrt {n}}}}$

Экстремальный принцип энтропии для фиксации свободного параметра ${\displaystyle \sigma }$[ править ]

В приложениях это параметр, который необходимо определить. Для процессов роста, уравновешенных производством и диссипацией, использование экстремального принципа энтропии Шеннона показывает, что ${\displaystyle \sigma }$

${\displaystyle {\begin{aligned}\sigma =1{\big /}{\sqrt {6}}\end{aligned}}}$ ^[40]

Затем это значение можно использовать для установления некоторого масштабного соотношения между точкой перегиба и точкой максимума логнормального распределения. ^[40] Это соотношение определяется основанием натурального логарифма , и демонстрирует геометрическое сходство с принципом минимальной поверхностной энергии. Эти масштабные соотношения полезны для прогнозирования ряда процессов роста (распространение эпидемии, разбрызгивание капель, рост населения, скорость вращения водоворота в ванне, распределение языковых символов, профиль скорости турбулентности и т. Д.). Например, логарифмически нормальная функция с таким хорошо согласуется с размером вторично образующихся капель во время удара капли ^[41] и распространения эпидемического заболевания. ^[42]${\displaystyle e=2.718\ldots }$${\displaystyle \sigma }$

Это значение используется для обеспечения вероятностного решения уравнения Дрейка. ^[43]${\displaystyle \sigma =1{\big /}{\sqrt {6}}}$

Возникновение и применение [ править ]

Логнормальное распределение важно при описании природных явлений. Многие процессы естественного роста обусловлены накоплением множества небольших процентных изменений, которые становятся добавочными в логарифмическом масштабе. При соответствующих условиях регулярности распределение результирующих накопленных изменений будет все более хорошо аппроксимироваться логнормальным, как отмечалось выше в разделе « Мультипликативная центральная предельная теорема ». Это также известно как закон Гибрата в честь Роберта Гибрата (1904–1980), который сформулировал его для компаний. ^[44]Если скорость накопления этих небольших изменений не меняется со временем, рост перестает зависеть от размера. Даже если это не так, распределение по размеру вещей, которые со временем растут, в любом возрасте имеет тенденцию быть логнормальным.

Второе обоснование основано на наблюдении, что фундаментальные законы природы подразумевают умножение и деление положительных переменных. Примерами могут служить простой закон гравитации, связывающий массы и расстояние с результирующей силой, или формула для равновесных концентраций химических веществ в растворе, которая связывает концентрации эдуктов и продуктов. Предположение о логнормальном распределении задействованных переменных приводит в этих случаях к согласованным моделям.

Даже если ни одно из этих обоснований не применимо, логнормальное распределение часто является правдоподобной и эмпирически адекватной моделью. Примеры включают следующее:

Человеческое поведение [ править ]

• Длина комментариев, размещаемых в дискуссионных форумах в Интернете, соответствует нормальному распределению. ^[45]
• Время, затрачиваемое пользователями на онлайн-статьи (анекдоты, новости и т. Д.), Распределено обычным образом. ^[46]
• Продолжительность шахматных партий имеет тенденцию к логнормальному распределению. ^[47]
• Продолжительность начала акустических сравнительных стимулов, которые соответствуют стандартному стимулу, подчиняется логнормальному распределению. ^[17]
• Кубик Рубика решает, как общие, так и индивидуальные, похоже, следует логнормальному распределению. ^[48]

В биологии и медицине [ править ]

• Меры размера живой ткани (длина, площадь кожи, вес). ^[49]
• Для высокоинфекционных эпидемий, таких как атипичная пневмония в 2003 г., если задействована политика контроля государственного вмешательства, показано, что количество госпитализированных случаев удовлетворяет логарифмически нормальному распределению без каких-либо свободных параметров, если предполагается энтропия и стандартное отклонение определяется принцип максимальной скорости производства энтропии. ^[50]
• Длина инертных придатков (волос, когтей, ногтей, зубов) биологических образцов в направлении роста. ^{[ необходима цитата ]}
• Нормализованное количество считываний RNA-Seq для любой области генома может быть хорошо аппроксимировано логнормальным распределением.
• Длина считывания последовательности PacBio соответствует логарифмически нормальному распределению. ^[51]
• Определенные физиологические измерения, такие как артериальное давление у взрослых людей (после разделения на мужские и женские субпопуляции). ^[52]
• В нейробиологии распределение частоты возбуждения в популяции нейронов часто приблизительно логнормально. Впервые это наблюдалось в коре и полосатом теле ^[53], а затем в гиппокампе и энторинальной коре ^[54] и в других частях мозга. ^{[55] [56]} Кроме того, собственные распределения усиления и распределения синаптических весов также кажутся логнормальными ^[57] .

В коллоидной химии и химии полимеров [ править ]

• Распределение частиц по размерам .
• Распределение молярной массы .

Следовательно, эталонные диапазоны для измерений у здоровых людей более точно оцениваются, предполагая логнормальное распределение, чем предполагая симметричное распределение относительно среднего.

Гидрология [ править ]

• В гидрологии логарифмически нормальное распределение используется для анализа экстремальных значений таких переменных, как месячные и годовые максимальные значения суточных осадков и объемов речного стока. ^[58]

Изображение справа, созданное с помощью CumFreq , иллюстрирует пример подгонки логнормального распределения к ранжированным годовым максимальным однодневным осадкам, показывающим также пояс 90% уверенности, основанный на биномиальном распределении . ^[59]

Данные об осадках представлены в виде графиков позиций как часть кумулятивного частотного анализа .

Социальные науки и демография [ править ]

• В экономике есть свидетельства того, что доход 97–99% населения распределяется логарифмически нормально. ^[60] (Распределение лиц с более высокими доходами следует распределению Парето ). ^[61]

• Если распределение доходов следует логнормальному распределению со стандартным отклонением , то коэффициент Джини , обычно используемый для оценки неравенства доходов, можно вычислить как где - функция ошибок (поскольку , где ${\displaystyle \sigma }$${\displaystyle G=\operatorname {erf} \left({\frac {\sigma }{2}}\right)}$${\displaystyle \operatorname {erf} }$${\displaystyle G=2\phi \left({\frac {\sigma }{\sqrt {2}}}\right)-1}$${\displaystyle \phi }$

• В финансах , в частности в модели Блэка – Шоулза , изменения логарифма обменных курсов, индексов цен и индексов фондовых рынков считаются нормальными ^[62] (эти переменные ведут себя как сложные проценты, а не как простые проценты, и поэтому являются мультипликативными). . Тем не менее, некоторые математики , такие как Бенуа Мандельброт утверждал ^[63] , что распределение лог-Леви , который обладает тяжелыми хвостами бы более подходящей моделью, в частности , для анализа на фондовом рынке аварий . В самом деле, распределение цен на акции обычно демонстрирует толстый хвост . ^[64] Распределение «толстых хвостов» изменений во время обвалов фондового рынка делает недействительными предположения центральной предельной теоремы .
• В наукометрии количество цитирований журнальных статей и патентов следует дискретному логнормальному распределению. ^{[65] [66]}
• Размеры города (население) удовлетворяют закону Гибрата. ^[67] Процесс роста размеров города пропорционален и инвариантен по отношению к размеру. Из центральной предельной теоремы , следовательно, логарифм размера города , как правило , распределены.

Технология [ править ]

• В анализе надежности логарифмически нормальное распределение часто используется для моделирования времени ремонта обслуживаемой системы. ^[68]
• В беспроводной связи «средняя локальная мощность, выраженная в логарифмических значениях, таких как дБ или непер, имеет нормальное (т. Е. Гауссово) распределение». ^[69] Кроме того, случайное препятствие радиосигналам из-за больших зданий и холмов, называемое затенением , часто моделируется как логнормальное распределение.
• Распределение частиц по размерам, полученное путем измельчения со случайными ударами, например, при шаровой мельнице . ^{[ необходима цитата ]}
• Распределение размеров общедоступных файлов аудио- и видеоданных ( типов MIME ) следует нормальному логарифмическому распределению на пять порядков величины . ^[70]
• В компьютерных сетях и анализе интернет-трафика нормальный логарифм показан как хорошая статистическая модель для представления количества трафика в единицу времени. Это было продемонстрировано применением надежного статистического подхода к большим группам реальных трассировок Интернета. В этом контексте нормальное логарифмическое распределение показало хорошую производительность в двух основных случаях использования: (1) прогнозирование доли времени, в течение которого трафик превысит заданный уровень (для согласования уровня обслуживания или оценки пропускной способности канала), т. Е. Определение размеров канала на основе полосы пропускания. обеспечение и (2) прогнозирование 95-го процентиля ценообразования. ^[71]

См. Также [ править ]

• Распределение с тяжелым хвостом
• Логарифмическая модель потерь на трассе
• Модифицированное логнормальное степенное распределение
• Медленное затухание

Примечания [ править ]