Из Википедии, свободной энциклопедии
Перейти к навигации Перейти к поиску
Не путать с Отомино .
369 бесплатных октимино

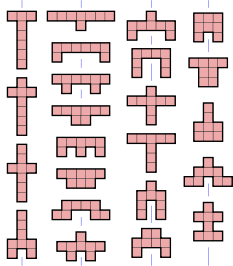
Октамин (или 8-omino ) является Полимином порядка 8, то есть многоугольник в плоскости выполнен из 8 одинаковых по размеру квадратов , соединенных от края до края. [1] Когда вращения и отражения не считаются отдельными формами, существует 369 различных свободных октимино. Когда отражения считаются отчетливыми, получается 704 односторонних октимино. Когда вращения также считаются отдельными, существует 2725 фиксированных октимино. [2] [3]

Симметрия [ править ]

На рисунке показаны все возможные свободные октамино, раскрашенные в соответствии с их группами симметрии :

  • 316 октамино (окрашены в серый цвет) не имеют симметрии . Их группа симметрии состоит только из тождественного отображения .
  • У 23 октимино (окрашенных в красный цвет) ось симметрии отражения совпадает с линиями сетки. Их группа симметрии состоит из двух элементов: тождества и отражения на линии, параллельной сторонам квадратов.
Отражение симметричных октимино 90 град.svg
  • 5 октимино (окрашены в зеленый цвет) имеют ось симметрии отражения под углом 45 ° к линиям сетки. Их группа симметрии состоит из двух элементов: тождества и диагонального отражения.
Отражение симметричных октимино 45 град.свг
  • 18 октимино (окрашены в синий цвет) обладают точечной симметрией, также известной как вращательная симметрия второго порядка. Их группа симметрии состоит из двух элементов: идентичности и поворота на 180 °.
Вращение симметричных октимино (C2) .svg
  • 1 октомино (желтого цвета) имеет вращательную симметрию четвертого порядка. Его группа симметрии состоит из четырех элементов, идентичности и вращения на 90 °, 180 ° и 270 °.
Вращение симметричного октомино (C4) .svg
  • 4 октамино (окрашены в фиолетовый цвет) имеют две оси симметрии отражения, обе выровнены с линиями сетки. Их группа симметрии состоит из четырех элементов: идентичности, двух отражений и поворота на 180 °. Это диэдральная группа порядка 2, также известная как четырехгруппа Клейна .
  • 1 октомино (оранжевого цвета) имеет две оси симметрии отражения, обе совмещенные с диагоналями. Его группа симметрии также является группой диэдра порядка 2 с четырьмя элементами.
  • 1 октомино (окрашенный в голубой цвет) имеет четыре оси симметрии отражения, выровненные с линиями сетки и диагоналями, и вращательную симметрию четвертого порядка. Его группа симметрии, двугранная группа порядка 4, состоит из восьми элементов.
Симметричные октамино вращения и отражения h.svg

Набор октимино - это самый низкий набор полимино, в котором реализованы все восемь возможных симметрий. Следующим более высоким набором с этим свойством является набор додекомино (12-омино). [3]

Если отражения октамино считаются отдельными, как в случае с односторонними октамино, то первая, четвертая и пятая категории выше удваиваются по размеру, что приводит к дополнительным 335 октимино, всего 704. Если вращения также считаются отдельными, затем октамино из первой категории засчитываются восьмикратно, из следующих трех категорий засчитываются четырехкратно, из категорий от пяти до семи учитываются дважды, а последнее октомино засчитывается только один раз. В результате получается 316 × 8 + (23 + 5 + 18) × 4 + (1 + 4 + 1) × 2 + 1 = 2725 фиксированных октимино.

Упаковка и укладка [ править ]

Из 369 бесплатных октимино 320 удовлетворяют критерию Конвея, а еще 23 могут образовывать патч, удовлетворяющий этому критерию. [4] Остальные 26 октимино (включая 6 с дырками) не могут составить мозаику на плоскости. [5]

Поскольку 6 бесплатных октимино имеют отверстие, легко доказать, что полный набор октимино не может быть упакован в прямоугольник и что не все октимино можно выложить плиткой .

Октомино с дырами.svg

Ссылки [ править ]

  1. ^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8.
  2. ^ Вайсштейн, Эрик В. "Octomino" . Материал из MathWorld - веб-ресурса Wolfram . Проверено 22 июля 2008 .
  3. ^ a b Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика . 36 (2): 191–203. DOI : 10.1016 / 0012-365X (81) 90237-5 .
  4. Перейти ↑ Rhoads, Glenn C. (2005). «Плоские мозаики полимино, полигексами и полиалмазами» . Журнал вычислительной и прикладной математики . 174 (2): 329–353. DOI : 10.1016 / j.cam.2004.05.002 .
  5. ^ Гарднер, Мартин (август 1975). «Еще о мозаике плоскости: возможности полимино, полиалмазов и полигексов». Scientific American . 233 (2): 112–115.