Орбитальные элементы

Орбитальные элементы - это параметры, необходимые для однозначной идентификации конкретной орбиты . В небесной механике эти элементы рассматриваются в системах двух тел с использованием орбиты Кеплера . Существует много различных способов математического описания одной и той же орбиты, но определенные схемы, каждая из которых состоит из набора из шести параметров, обычно используются в астрономии и орбитальной механике .

Реальная орбита и ее элементы меняются со временем из-за гравитационных возмущений других объектов и эффектов общей теории относительности . Орбита Кеплера - это идеализированная математическая аппроксимация орбиты в определенное время.

Кеплеровские элементы [ редактировать ]

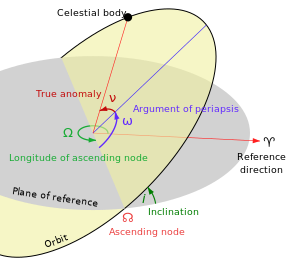
На этой диаграмме плоскость орбиты (желтая) пересекает базовую плоскость (серая). Для спутников на околоземной орбите базовой плоскостью обычно является экваториальная плоскость Земли, а для спутников на солнечных орбитах - плоскость эклиптики . Пересечение называется линией узлов , так как оно соединяет центр масс с восходящими и нисходящими узлами. Базовая плоскость вместе с весенней точкой ( ♈︎ ) устанавливает систему отсчета.

Традиционные элементы орбиты - это шесть кеплеровских элементов после Иоганна Кеплера и его законов движения планет .

Если смотреть с инерциальной системы отсчета , два вращающихся тела имеют разные траектории. Каждая из этих траекторий имеет фокус в общем центре масс . Если смотреть из неинерциальной системы отсчета, центрированной на одном из тел, видна только траектория противоположного тела; Кеплеровы элементы описывают эти неинерциальные траектории. Орбита имеет два набора кеплеровских элементов в зависимости от того, какое тело используется в качестве точки отсчета. Базовое тело (обычно самое массивное) называется первичным , другое тело - вторичным . Первичный элемент не обязательно обладает большей массой, чем вторичный, и даже когда тела имеют равную массу, элементы орбиты зависят от выбора первичного.

Два элемента определяют форму и размер эллипса:

Эксцентриситет ( $e$ ) - форма эллипса, описывающая, насколько он удлинен по сравнению с кругом (не отмечен на диаграмме).
Большая полуось ( $а$ ) - сумма перицентрического и апоцентрического расстояний, деленная на два. Для классических орбит двух тел большая полуось - это расстояние между центрами тел, а не расстояние между телами от центра масс.

Два элемента определяют ориентацию орбитальной плоскости, в которую вложен эллипс:

Наклон ( $i$ ) - вертикальный наклон эллипса относительно плоскости отсчета, измеренный в восходящем узле (где орбита проходит вверх через плоскость отсчета, зеленый угол $i$ на диаграмме). Угол наклона измеряется перпендикулярно линии пересечения плоскости орбиты и плоскости отсчета. Любые три точки на эллипсе будут определять плоскость орбиты эллипса. Плоскость и эллипс - это двухмерные объекты, определенные в трехмерном пространстве.
Долгота восходящего узла ( $Ом$ ) - горизонтально ориентирует восходящий узел эллипса (где орбита проходит вверх через базовую плоскость, символизируемый $☊$ ) относительно опорного кадра в весеннем точке (символизируемом ♈︎). Он измеряется в базовой плоскости и показан на диаграмме как зеленый угол $Ω$ .

Остальные два элемента следующие:

Аргумент перицентра ( $ω$ ) определяет ориентацию эллипса в плоскости орбиты, как угол, измеренный от восходящего узла к перицентру (ближайшая точка, в которой объект-спутник подходит к основному объекту, вокруг которого он вращается, синий угол $ω$ в диаграмму).
Истинная аномалия ( $ν$ , $θ$ или $f$ ) в эпоху ( $t 0$ ) определяет положение орбитального тела вдоль эллипса в определенное время («эпоху»).

Средняя аномалия $M$ является математически удобным фиктивным «углом» , который изменяется линейно со временем, но не соответствует реальному геометрическому углу. Его можно преобразовать в истинную аномалию $ν$ , которая действительно представляет собой реальный геометрический угол в плоскости эллипса между перицентром (самый близкий подход к центральному телу) и положением орбитального объекта в любой момент времени. Таким образом, истинная аномалия показана на диаграмме как красный угол $ν$ , а средняя аномалия не показана.

Углы наклона, долготы восходящего узла и аргумент перицентра также могут быть описаны как углами Эйлера , определяющей ориентацию орбиты по отношению к эталонной системе координат.

Обратите внимание, что неэллиптические траектории также существуют, но они не замкнуты и, следовательно, не являются орбитами. Если эксцентриситет больше единицы, траектория является гиперболой . Если эксцентриситет равен единице, а угловой момент равен нулю, траектория является радиальной . Если эксцентриситет равен единице и есть угловой момент, траектория представляет собой параболу .

Обязательные параметры [ править ]

Учитывая инерциальную систему отсчета и произвольную эпоху (заданный момент времени), необходимы ровно шесть параметров, чтобы однозначно определить произвольную и невозмущенную орбиту.

Это потому, что задача содержит шесть степеней свободы . Они соответствуют трем пространственным измерениям, которые определяют положение ( $x$ , $y$ , $z$ в декартовой системе координат ), плюс скорость в каждом из этих измерений. Их можно описать как векторы орбитального состояния , но это часто неудобный способ представления орбиты, поэтому вместо них обычно используются кеплеровские элементы.

Иногда эпоху считают «седьмым» орбитальным параметром, а не частью системы отсчета.

Если эпоха определяется как момент, когда один из элементов равен нулю, количество неопределенных элементов уменьшается до пяти. (Шестой параметр по-прежнему необходим для определения орбиты; он просто численно устанавливается на ноль по соглашению или «перемещается» в определение эпохи по отношению к реальным часам.)

Альтернативные параметризации [ править ]

Кеплеровские элементы могут быть получены из векторов орбитального состояния (трехмерный вектор для положения и другой для скорости) путем ручных преобразований или с помощью компьютерного программного обеспечения. ^[1]

Другие параметры орбиты могут быть вычислены из кеплеровских элементов, таких как период , апоапсис и перицентр . (При обращении вокруг Земли последние два члена известны как апогей и перигей.) Обычно в наборах кеплеровских элементов указывается период вместо большой полуоси, поскольку каждый из них может быть вычислен на основе другого при условии стандартной гравитационной параметр , $ГМ$ , дается для центрального тела.

Вместо средней аномалии в эпоху могут использоваться средняя аномалия $M$ , средняя долгота , истинная аномалия $ν 0$ или (редко) эксцентрическая аномалия .

Использование, например, «средней аномалии» вместо «средней аномалии в эпоху» означает, что время $t$ должно быть указано как седьмой элемент орбиты. Иногда предполагается, что средняя аномалия равна нулю в эпоху (путем выбора соответствующего определения эпохи), оставляя только пять других орбитальных элементов, которые необходимо указать.

Для разных астрономических тел используются разные наборы элементов. Эксцентриситет $e$ и либо большая полуось, $a$ , либо расстояние до перицентра $q$ , используются для определения формы и размера орбиты. Долгота восходящего узла, $Ом$ , наклон, $I$ , и аргумент перицентре, $со$ , или долготой перицентре, $П$ , задающие ориентацию орбиты в ее плоскости. Либо долгота в эпоху, $L 0$ , средняя аномалия в эпоху, $M 0$ , либо время прохождения перигелия, $T 0$ , используются для указания известной точки на орбите. Сделанный выбор зависит от того, используется ли весеннее равноденствие или узел в качестве основного ориентира. Большая полуось известна, если известны среднее движение и гравитационная масса . ^[2]^[3]

Также довольно часто можно увидеть либо среднюю аномалию ( $M$ ), либо среднюю долготу ( $L$ ), выраженные напрямую, без промежуточных шагов $M 0$ или $L 0$ , как полиномиальную функцию по времени. Этот метод выражения объединит среднее движение ( $n$ ) в полином как один из коэффициентов. Похоже, что $L$ или $M$ выражаются более сложным образом, но нам понадобится на один элемент орбиты меньше.

Среднее движение также может быть скрыто за цитатами орбитального периода $P$ . ^{[ требуется разъяснение ]}

Наборы орбитальных элементов
Объект	Используемые элементы
Большая планета	$е, а, я , Ω , ϖ , L 0$
Комета	$e, q , i, Ω, ω , T 0$
Астероид	$е, а, я, Ω, ω , M 0$
Двухстрочные элементы	$е, я, Ω, ω, n , M 0$

Преобразования угла Эйлера [ править ]

Углы $Ω$ , $i$ , $ω$ - это углы Эйлера (соответствующие $α$ , $β$ , $γ$ в обозначениях, используемых в этой статье), характеризующие ориентацию системы координат.

$x̂$ , $ŷ$ , $ẑ$ из инерциальной системы координат $Î$ , $Ĵ$ , $K̂$

куда:

$Î$ , $Ĵ$ находится в экваториальной плоскости центрального тела. $Î$ находится в направлении весеннего равноденствия. $Ĵ$ перпендикулярна $Î$ и $Î$ определяет опорную плоскость. $K̂$ перпендикулярен плоскости отсчета. Орбитальные элементы тел (планет, комет, астероидов ...) в Солнечной системе обычно используют эклиптику в качестве этой плоскости.
$x̂$ , $ŷ$ находятся в плоскости орбиты, а $x̂ -$ в направлении к перицентру ( перицентру ). $ẑ$ перпендикулярно плоскости орбиты. $ŷ$ взаимно перпендикулярно $x̂$ и $ẑ$ .

Тогда преобразование системы координат $Î$ , $Ĵ$ , $K̂ в систему$ координат $x̂$ , $ŷ$ , $ẑ$ с углами Эйлера $Ω$ , $i$ , $ω$ имеет вид:

{\ Displaystyle {\ begin {align} x_ {1} & = \ cos \ Omega \ cdot \ cos \ omega - \ sin \ Omega \ cdot \ cos i \ cdot \ sin \ omega \; \\ x_ {2} & = \ sin \ Omega \ cdot \ cos \ omega + \ cos \ Omega \ cdot \ cos i \ cdot \ sin \ omega \; \\ x_ {3} & = \ sin i \ cdot \ sin \ omega; \\\ , \\ y_ {1} & = - \ cos \ Omega \ cdot \ sin \ omega - \ sin \ Omega \ cdot \ cos i \ cdot \ cos \ omega \; \\ y_ {2} & = - \ sin \ Омега \ cdot \ sin \ omega + \ cos \ Omega \ cdot \ cos i \ cdot \ cos \ omega \; \\ y_ {3} & = \ sin i \ cdot \ cos \ omega \; \\\, \\ z_ {1} & = \ sin i \ cdot \ sin \ Omega \; \\ z_ {2} & = - \ sin i \ cdot \ cos \ Omega \; \\ z_ {3} & = \ cos i \; \\\, \ end {выровнен}}}

\left[{\begin{array}{ccc}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2}&z_{3}\end{array}}\right]=\left[{\begin{array}{ccc}\cos \omega &\sin \omega &0\\-\sin \omega &\cos \omega &0\\0&0&1\end{array}}\right]\,\left[{\begin{array}{ccc}1&0&0\\0&\cos i&\sin i\\0&-\sin i&\cos i\end{array}}\right]\,\left[{\begin{array}{ccc}\cos \Omega &\sin \Omega &0\\-\sin \Omega &\cos \Omega &0\\0&0&1\end{array}}\right]\,;

куда

{\begin{aligned}\mathbf {\hat {x}} &=x_{1}\mathbf {\hat {I}} +x_{2}\mathbf {\hat {J}} +x_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {y}} &=y_{1}\mathbf {\hat {I}} +y_{2}\mathbf {\hat {J}} +y_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {z}} &=z_{1}\mathbf {\hat {I}} +z_{2}\mathbf {\hat {J}} +z_{3}\mathbf {\hat {K}} ~.\\\,\end{aligned}}

Обратное преобразование, которое вычисляет 3 координаты в системе IJK с учетом 3 (или 2) координат в системе xyz, представлено обратной матрицей. Согласно правилам матричной алгебры , матрица , обратная произведению трех матриц вращения, получается путем инвертирования порядка трех матриц и переключения знаков трех углов Эйлера.

Преобразование из $x̂$ , $ŷ$ , $ẑ$ в углы Эйлера $Ω$ , $i$ , $ω$ :

{\begin{aligned}\Omega &=\operatorname {arg} \left(-z_{2},z_{1}\right)\\i&=\operatorname {arg} \left(z_{3},{\sqrt {{z_{1}}^{2}+{z_{2}}^{2}}}\right)\\\omega &=\operatorname {arg} \left(y_{3},x_{3}\right)\\\,\end{aligned}}

где $arg (x, y)$ обозначает полярный аргумент, который может быть вычислен с помощью стандартной функции atan2 (y, x), доступной во многих языках программирования.

Предсказание орбиты [ править ]

В идеальных условиях идеально сферического центрального тела и нулевых возмущений все элементы орбиты, кроме средней аномалии, являются постоянными. Средняя аномалия изменяется линейно со временем, масштабируемая средним движением , ^[2]

n={\sqrt {\frac {\mu }{a^{3}}}}.

Следовательно, если в любой момент $t 0$ параметры орбиты равны $[e 0, a 0, i 0, Ω 0, ω 0, M 0]$ , то элементы в момент времени $t = t 0 + δt$ задаются как $[e 0, a 0, i 0, Ω 0, ω 0, M 0 + n δt]$

Возмущения и элементарная дисперсия [ править ]

Невозмутимая, два тела , ньютоновская орбита всегда конические сечения , поэтому кеплеровы элементы определяют эллипс , параболу или гиперболу . Реальные орбиты имеют возмущения, поэтому данный набор кеплеровских элементов точно описывает орбиту только в эпоху. Эволюция элементов орбиты происходит из-за гравитационного притяжения тел, отличных от первичного, несферичности первичного тела, атмосферного сопротивления , релятивистских эффектов , радиационного давления , электромагнитных сил и т. Д.

Кеплеровские элементы часто можно использовать для получения полезных прогнозов, иногда близких к эпохе. В качестве альтернативы, реальные траектории могут быть смоделированы как последовательность кеплеровских орбит, которые соприкасаются («целуют» или касаются) реальной траектории. Их также можно описать так называемыми планетарными уравнениями , дифференциальными уравнениями, которые имеют различные формы, разработанные Лагранжем , Гауссом , Делоне , Пуанкаре или Хиллом .

Двухстрочные элементы [ править ]

Параметры кеплеровских элементов можно закодировать в виде текста в нескольких форматах. Наиболее распространенным из них является формат «двухстрочных элементов» (TLE) NASA / NORAD ^[4], первоначально разработанный для использования с перфокартами на 80 столбцов, но все еще используемый, поскольку это наиболее распространенный формат, и с ним можно работать. легко и со всеми современными хранилищами данных.

В зависимости от приложения и орбиты объекта данные, полученные из TLE старше 30 дней, могут стать ненадежными. Орбитальные позиции могут быть вычислены из Тлеса через ПМГ / SGP4 / SDP4 / SGP8 / SDP8 алгоритмов. ^[5]

Пример двухстрочного элемента: ^[6]

1 27651U 03004A 07083.49636287 .00000119 00000-0 30706-4 0 26922 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

Переменные Делоне [ править ]

Орбитальные элементы Делоне были введены Шарлем-Эженом Делоне во время его изучения движения Луны . ^[7] Обычно называемые переменными Делоне , они представляют собой набор канонических переменных , которые представляют собой координаты действие-угол . Углы представляют собой простые суммы некоторых углов Кеплара:

$\ell =M+\omega +\Omega ~:$ средняя долгота
$g=\omega +\Omega ~:$ долгота перицентра и
$h=\Omega ~:$ долгота восходящего узла

наряду с их соответствующими сопряженными импульсами , $L$ , $G$ и $H$ . ^[8] Импульсы $L$ , $G$ и $H$ являются переменными действия и представляют собой более сложные комбинации кеплеровских элементов $a$ , $e$ и $i$ .

Переменные Делоне используются для упрощения пертурбативных вычислений в небесной механике, например, при исследовании колебаний Козая – Лидова в иерархических тройных системах. ^[8] Преимущество переменных Делоне состоит в том, что они остаются четко определенными и неособыми (за исключением $h$ , что можно допустить), когда $e$ и / или $i$ очень малы: когда орбита пробной частицы почти круглая ( ) , или почти «плоский» ( ). $e\approx 0$ $i\approx 0$

См. Также [ править ]

Семейство астероидов, астероиды с одинаковыми собственными орбитальными элементами
Бета угол
Эфемериды
Геопотенциальная модель
Векторы орбитального состояния
Правильные элементы орбиты
Оскулирующая орбита

Ссылки [ править ]

^ Например, с "VEC2TLE" . amsat.org .
^ a b Грин, Робин М. (1985). Сферическая астрономия . Издательство Кембриджского университета. ISBN 978-0-521-23988-2.
^ Дэнби, JMA (1962). Основы небесной механики . Вильманн-Белл. ISBN 978-0-943396-20-0.
^ Келсо, TS "Часто задаваемые вопросы: формат набора двухстрочных элементов" . celestrak.com . CelesTrak. Архивировано из оригинального 26 марта 2016 года . Дата обращения 15 июня 2016 .
^ Зайдельманн, КП, изд. (1992). Пояснительное приложение к астрономическому альманаху (1-е изд.). Милл-Вэлли, Калифорния: Университетские научные книги.
^ "SORCE" . Heavens-Above.com . данные об орбите. Архивировано из оригинального 27 сентября 2007 года.
Перейти ↑ Aubin, David (2014). «Делоне, Шарль-Эжен». Биографическая энциклопедия астрономов . Нью-Йорк, Нью-Йорк: Springer New York. С. 548–549. DOI : 10.1007 / 978-1-4419-9917-7_347 . ISBN 978-1-4419-9916-0.
^ а б Шевченко, Иван (2017). Эффект Лидова – Козаи: приложения в исследовании экзопланет и динамической астрономии . Чам: Спрингер. ISBN 978-3-319-43522-0.

Внешние ссылки [ править ]

Гурфил, Пини (2005). «Параметры Эйлера как неособые элементы орбиты в приэкваториальных орбитах». J. Guid. Contrl. Динамика . 28 (5). Bibcode : 2005JGCD ... 28.1079G . DOI : 10.2514 / 1.14760 .

В Викиучебнике есть книга по теме: Астродинамика / Классические элементы орбиты.

«Учебник» . АМСАТ . Кеплеровские элементы. Архивировано из оригинального 14 октября 2002 года.

"Учебник по орбитам" . marine.rutgers.edu .

«Визуализатор орбитальных элементов» . orbitalmechanics.info .

Отчет № 3 (PDF) . celestrak (Отчет). Космический путь. Североамериканское командование воздушно-космической обороны (НОРАД). - серьезное лечение орбитальных элементов

«FAQ» . Celestrak . Двухстрочные элементы. Архивировано из оригинального 26 марта 2016 года.

«Онлайн-эфемериды JPL HORIZONS» . - также поставляет элементы орбиты для большого количества объектов солнечной системы

«Средние параметры орбиты» . ssd.jpl.nasa.gov . Планетарные спутники. Лаборатория реактивного движения / НАСА.

«Введение в экспорт» . ssd.jpl.nasa.gov . Планетарные и лунные эфемериды JPL. Лаборатория реактивного движения / НАСА.

«Векторы состояния: VEC2TLE» . MindSpring (программное обеспечение). Архивировано из оригинала 3 марта 2016 года. - доступ к ПО VEC2TLE

«Функция 'iauPlan94 ' » ( исходный код программного обеспечения C ). Библиотека SOFA C МАС. - элементы орбит больших планет

[1] Например, с "VEC2TLE" . amsat.org .

[Green-2] Грин, Робин М. (1985). Сферическая астрономия . Издательство Кембриджского университета. ISBN 978-0-521-23988-2.

[Danby-3] Дэнби, JMA (1962). Основы небесной механики . Вильманн-Белл. ISBN 978-0-943396-20-0.

[Kelso_FAQ-4] Келсо, TS "Часто задаваемые вопросы: формат набора двухстрочных элементов" . celestrak.com . CelesTrak. Архивировано из оригинального 26 марта 2016 года . Дата обращения 15 июня 2016 .

[5] Зайдельманн, КП, изд. (1992). Пояснительное приложение к астрономическому альманаху (1-е изд.). Милл-Вэлли, Калифорния: Университетские научные книги.

[6] "SORCE" . Heavens-Above.com . данные об орбите. Архивировано из оригинального 27 сентября 2007 года.

[Aubin-2014-7] Перейти ↑ Aubin, David (2014). «Делоне, Шарль-Эжен». Биографическая энциклопедия астрономов . Нью-Йорк, Нью-Йорк: Springer New York. С. 548–549. DOI : 10.1007 / 978-1-4419-9917-7_347 . ISBN 978-1-4419-9916-0.

[Shevchenko-2017-8] а б Шевченко, Иван (2017). Эффект Лидова – Козаи: приложения в исследовании экзопланет и динамической астрономии . Чам: Спрингер. ISBN 978-3-319-43522-0.