| 3-7 кисромбиль | |
|---|---|
 | |
| Тип | Двойственное полурегулярное гиперболическое разбиение |
| Лица | Прямоугольный треугольник |
| Края | Бесконечный |
| Вершины | Бесконечный |
| Диаграмма Кокстера | |
| Группа симметрии | [7,3], (* 732) |
| Группа вращения | [7,3] + , (732) |
| Двойной многогранник | Усеченная трехгептагональная черепица |
| Конфигурация лица | V4.6.14 |
| Характеристики | лицо-переходный |
| Викискладе есть медиафайлы, связанные с однородной двойной мозаикой V 4-6-14 . |
В геометрии , то 3-7 kisrhombille плиточное является полурегулярен двойным плиточным гиперболической плоскостью . Он построен из конгруэнтных прямоугольных треугольников с 4, 6 и 14 треугольниками, пересекающимися в каждой вершине.
Изображение показывает проекцию модели диска Пуанкаре на гиперболическую плоскость.
Он помечен как V4.6.14, потому что каждая грань прямоугольного треугольника имеет три типа вершин: один с 4 треугольниками, один с 6 треугольниками и один с 14 треугольниками. Это двойная мозаика усеченной трехгептагональной мозаики, которая имеет один квадрат, один семиугольник и один четырехугольник в каждой вершине.
Именование [ править ]
Название 3-7 кисромбиль дал Конвей , рассматривая его как ромбическую мозаику 3-7, разделенную оператором kis , добавив центральную точку к каждому ромбу и разделив ее на четыре треугольника.
Симметрия [ править ]
Подгруппы удаления зеркала в [7,3] отсутствуют. Единственная подгруппа с малым индексом - это альтернирование, [7,3] + , (732).
| Тип | Отражающий | Вращательный |
|---|---|---|
| индекс | 1 | 2 |
| Диаграмма |  |  |
| Кокстер ( орбифолд ) | [7,3] = (* 732) | [7,3] + = (732) |
Связанные многогранники и мозаики [ править ]
Три изоэдральных (правильных или квазирегулярных) мозаики могут быть построены из этого тайлинга путем объединения треугольников:
| Модель диска Пуанкаре |  |  |  |
|---|---|---|---|
| Центр | Семиугольник | Треугольник | Ромбический |
| Модель диска Клейна |  |  |  |
| Связанная черепица |  |  | 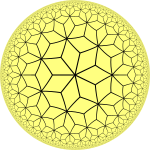 |
| Семиугольная черепица | Треугольная черепица | Ромбическая черепица |
| Равномерная семиугольная / треугольная мозаика | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [7,3], (* 732) | [7,3] + , (732) | ||||||||||
 |  | ||||||||||
| {7,3} | т {7,3} | г {7,3} | т {3,7} | {3,7} | рр {7,3} | tr {7,3} | sr {7,3} | ||||
| Униформа двойников | |||||||||||
| V7 3 | V3.14.14 | V3.7.3.7 | V6.6.7 | V3 7 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Он топологически связан с последовательностью многогранников; см. обсуждение . Эта группа является особенной тем, что у каждой вершины четное число ребер и образуют биссектрисы, проходящие через многогранники и бесконечные прямые на плоскости, и являются областями отражения для групп треугольников (2,3, n ) - для семиугольной мозаики важная (2,3,7) треугольная группа .
См. Также равномерные мозаики гиперболической плоскости с симметрией (2, 3, 7) .
Плитки кисромбилли можно увидеть как из последовательности мозаик ромбилей, начиная с куба, с гранями, разделенными или поцелованными в углах центральной точкой грани.
| * n 32 мутации симметрии полностью усеченных мозаик : 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. * n 32 [ n , 3] | Сферический | Евклид. | Компактная гиперб. | Paraco. | Некомпактный гиперболический | |||||||
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] | * ∞32 [∞, 3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры | ||||||||||||
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | ||||||||||||
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Так же, как группа треугольников (2,3,7) является фактором модулярной группы (2,3, ∞), ассоциированная мозаика является фактором модульной мозаики, как показано на видео справа.
Ссылки [ править ]
- ^ Платоновы мозаики римановых поверхностей: Модульная группа , Жерар Вестендорп
- Джон Х. Конвей , Хайди Берджел, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
См. Также [ править ]
- Треугольная черепица Hexakis
- Замощения правильных многоугольников
- Список однородных мозаик
- Равномерные мозаики в гиперболической плоскости