Шестигранник Тетракис

Шестигранник Тетракис
(Нажмите здесь, чтобы повернуть модель)
Тип	Каталонский твердый
Диаграмма Кокстера
Обозначение Конвея	kC
Тип лица	V4.6.6 равнобедренный треугольник
Лица	24
Края	36
Вершины	14
Вершины по типу	6 {4} +8 {6}
Группа симметрии	O _h , B ₃ , [4,3], (* 432)
Группа вращения	О, [4,3] ⁺ , (432)
Двугранный угол	143 ° 07′48 ″ arccos (-4/5)
Характеристики	выпуклый, гранно-транзитивный
Усеченный октаэдр ( двойственный многогранник )	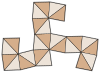Сеть

Двойное соединение из усеченного октаэдра и тетракисгексаэдра. Ксилография слева - из Perspectiva Corporum Regularium (1568 г.) Венцеля Ямницера .

Матрица и модель кристалла

Чертеж и модель кристалла варианта с тетраэдрической симметрией, называемого тетраэдром гексакиса ^[1]

В геометрии , A тетракис шестигранник (также известный как tetrahexahedron , hextetrahedron , тетракис куб и kiscube ^[2] ) является Каталонским твердым веществом . Его двойник - усеченный октаэдр , архимедово твердое тело .

Это также можно назвать disdyakis шестигранник или гексакис тетраэдр как двойной из omnitruncated тетраэдра .

Декартовы координаты [ править ]

Декартовы координаты 14 вершин четырехугольного шестигранника с центром в начале координат - это точки (± 3/2, 0, 0), (0, ± 3/2, 0), (0, 0, ± 3/2) и (± 1, ± 1, ± 1).

Длина более коротких ребер этого тетракис-гексаэдра равна 3/2, а длина более длинных ребер равна 2. Грани представляют собой острые равнобедренные треугольники. У них больший угол и два меньших равны . ${\ Displaystyle \ arccos (1/9) \ приблизительно 83.620 \, 629 \, 791 \, 56 ^ {\ circ}}$ ${\ Displaystyle \ arccos (2/3) \ приблизительно 48.189 \, 685 \, 104 \, 22 ^ {\ circ}}$

Ортогональные проекции [ править ]

Тетракисгексаэдр , двойной из усеченного октаэдра имеет 3 позиции симметрии, две расположенные на вершинах и один в середине края.

Ортогональные проекции
Проективная симметрия	[2]	[4]	[6]
Шестигранник Тетракис
Усеченный октаэдр

Использует [ редактировать ]

Природные ( кристаллические ) образования тетрагексаэдров наблюдаются в системах меди и флюорита .

Полиэдральные кости в форме , как тетракисгексаэдр иногда используются игроками .

24-клетки рассматриваются под вершиной первой перспективной проекции имеют поверхностную топологию тетракисгексаэдра и геометрические пропорции ромбического додекаэдра , с ромбическими гранями , разделенных на два треугольник.

Тетракис-шестигранник является одним из простейших примеров в теории строительства . Рассмотрим риманово симметрическое пространство, ассоциированное с группой SL 4 ( R ) . Его граница Титса имеет структуру сферического здания , квартиры которого представляют собой двумерные сферы. Разделение этой сферы на сферические симплексы (камеры) можно получить, взяв радиальную проекцию тетракис-шестигранника.

Симметрия [ править ]

При T _d , [3,3] (* 332) тетраэдрической симметрии треугольные грани представляют 24 фундаментальных домена тетраэдрической симметрии. Этот многогранник можно построить из 6 больших окружностей на сфере. Его также можно увидеть по кубу, квадратные грани которого триангулированы по вершинам и центрам граней, и по тетраэдру, грани которого разделены вершинами, средними ребрами и центральной точкой.


Усеченный tetratetrahedron	Disdyakis шестигранники	Дельтоидальный додекаэдр	Ромбический шестигранник	Тетраэдр

Сферический многогранник

(см. вращающуюся модель )	Ортографические проекции с 2-х, 3-х и 4-х кратных осей

Края сферического тетракисгексаэдр принадлежит шесть больших кругов, которые соответствуют зеркальным плоскостям в тетраэдрической симметрии . Их можно сгруппировать в три пары ортогональных окружностей (которые обычно пересекаются по одной координатной оси каждая). На изображениях ниже эти квадратные хозоэдры окрашены в красный, зеленый и синий цвета.

Стереографические проекции
	2-кратный	3-кратный	4-кратный

Размеры [ править ]

Если обозначить длину ребра базового куба буквой a , высота каждой вершины пирамиды над кубом будет равнаа/4. Наклон каждой треугольной грани пирамиды относительно грани куба является арктангенсом (1/2), примерно 26,565 ° (последовательность A073000 в OEIS ). Один край равнобедренных треугольников имеет длину a , два других - длину3 а/4, что следует из применения теоремы Пифагора к высоте и длине основания. Это дает высоту√ 5 а/4в треугольнике ( OEIS : A204188 ). Его площадь составляет√ 5 а/8, а внутренние углы - arccos (2/3) (приблизительно 48,1897 °) и дополнительные 180 ° - 2 arccos (2/3) (примерно 83,6206 °).

Объем пирамиды составляета ³/12; Таким образом, общий объем шести пирамид и куба в шестиграннике равен3 а ³/2.

Kleetope [ править ]

Его можно рассматривать как куб с квадратными пирамидами, покрывающими каждую квадратную грань; то есть это Kleetope куба.

Кубическая пирамида [ править ]

Это очень похоже на трехмерную сеть для четырехмерной кубической пирамиды , поскольку сетка для квадрата представляет собой квадрат с треугольниками, прикрепленными к каждому краю, сеть для кубической пирамиды - это куб с квадратными пирамидами, прикрепленными к каждой грани.

Связанные многогранники и мозаики [ править ]

Однородные октаэдрические многогранники
Симметрия : [4,3], (* 432)							[4,3] ⁺ (432)	[1 ⁺ , 4,3] = [3,3] (* 332)		[3 ⁺ , 4] (3 * 2)
{4,3}	т {4,3}	г {4,3} г {3 ^1,1 }	т {3,4} т {3 ^1,1 }	{3,4} {3 ^1,1 }	rr {4,3} s ₂ {3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	ч 2 {4,3} т {3,3}	с {3,4} с {3 ^1,1 }

		знак равно	знак равно	знак равно				знак равно или же	знак равно или же	знак равно

Двойники к однородным многогранникам
V4 3	V3.8 2	В (3,4) 2	V4.6 2	V3 4	V3.4 3	V4.6.8	V3 4 .4	V3 3	V3.6 2	V3 5

* n 32 мутация симметрии усеченных мозаик : n .6.6 v т е
Сим. * n 42 [n, 3]	Сферический				Евклид.	Компактный		Parac.	Некомпактный гиперболический
Сим. * n 42 [n, 3]	* 232 [2,3]	* 332 [3,3]	* 432 [4,3]	* 532 [5,3]	* 632 [6,3]	* 732 [7,3]	* 832 [8,3] ...	* ∞32 [∞, 3]	[12i, 3]	[9i, 3]	[6i, 3]
Усеченные фигуры
Конфиг.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
цифры n-kis
Конфиг.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Это многогранники в последовательности, определяемой конфигурацией граней V4.6.2 n . Эта группа особенная тем, что у нее есть все четное число ребер на вершину и образуют биссектрисы, проходящие через многогранники и бесконечные прямые на плоскости, и переходят в гиперболическую плоскость для любого n ≥ 7.

С четным числом граней в каждой вершине эти многогранники и мозаики можно показать, чередуя два цвета, чтобы все смежные грани имели разные цвета.

Каждая грань на этих областях также соответствует фундаментальной области группы симметрии с зеркалами порядка 2, 3, n в каждой вершине треугольной грани.

* n 32 мутации симметрии полностью усеченных мозаик : 4.6.2n v т е
Сим. * n 32 [ n , 3]	Сферический				Евклид.	Компактная гипербола.		Paraco.	Некомпактный гиперболический
Сим. * n 32 [ n , 3]	* 232 [2,3]	* 332 [3,3]	* 432 [4,3]	* 532 [5,3]	* 632 [6,3]	* 732 [7,3]	* 832 [8,3]	* ∞32 [∞, 3]	[12i, 3]	[9i, 3]	[6i, 3]	[3i, 3]
Цифры
Конфиг.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Конфиг.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

См. Также [ править ]

Триаконтаэдр Дисдякиса
Додекаэдр Дисдякиса
Kisrhombille плитка
Соединение трех октаэдров
Дельтоидный икоситетраэдр , еще одно 24- гранное каталонское тело.

Ссылки [ править ]

^ Hexakistetraeder на немецком, смотритенапример , Meyers страницу и Брокгауз страницу . На том же чертеже появляется в Брокгауза и Ефрона как преломленный пирамидальный тетраэдр ( преломляется пирамидальной тетраэдр ).
^ Conway, Симметрии вещей , с.284

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X. (Раздел 3-9)
Веннингер, Магнус (1983), двойные модели , Cambridge University Press , DOI : 10.1017 / CBO9780511569371 , ISBN 978-0-521-54325-5, Руководство по ремонту 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники, Тетракишексаэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5 [1] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 284, шестигранник Тетракиса )

Внешние ссылки [ править ]

Эрик В. Вайсштейн , шестигранник Тетракиса ( каталонское твердое тело ) в MathWorld .
Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- Модель VRML
- Обозначение Конвея для многогранников Попробуйте: "dtO" или "kC"
Tetrakis Hexahedron - Интерактивная модель многогранника
Равномерные многогранники

[1] Hexakistetraeder на немецком, смотритенапример , Meyers страницу и Брокгауз страницу . На том же чертеже появляется в Брокгауза и Ефрона как преломленный пирамидальный тетраэдр ( преломляется пирамидальной тетраэдр ).

[2] Conway, Симметрии вещей , с.284

[1]