В геометрии , А регулярная перекос apeirohedron является бесконечным регулярным перекос полиэдр , либо с косых правильными гранями или косых регулярных фигур вершин .
История [ править ]
По словам Кокстера , в 1926 году Джон Флиндерс Петри обобщил концепцию правильных косых многоугольников (неплоских многоугольников) на конечные правильные косые многогранники в 4-х измерениях и бесконечные правильные косые апейроэдры в 3-х измерениях (описанные здесь).
Кокстер выделил 3 формы с плоскими гранями и скошенными вершинами , две из которых дополняют друг друга. Все они названы модифицированным символом Шлефли { l , m | n }, где есть l -угольные грани, m граней вокруг каждой вершины, с отверстиями, идентифицированными как n -угольные отсутствующие грани.
Кокстер предложил модифицированный символ Шлефли { l , m | n } для этих фигур, причем { l , m } подразумевает фигуру вершины , m l-угольников вокруг вершины и n -угольных отверстий. Их вершинные фигуры представляют собой косые многоугольники , зигзагообразные между двумя плоскостями.
Правильные косые многогранники, представленные { l , m | n }, следуйте этому уравнению:
- 2 sin ( π / l ) · sin ( π / m ) = cos ( π / n )
Правильные косые апейроэдры евклидова 3-мерного пространства [ править ]
Три евклидовых решения в трехмерном пространстве: {4,6 | 4}, {6,4 | 4} и {6,6 | 3}. Джон Конвей назвал их mucube, muoctahedron и mutetrahedron соответственно для множественного куба, октаэдра и тетраэдра. [1]
- Mucube : {4,6 | 4}: 6 квадратов на вершине (связанных с кубическими сотами , построенными из кубических ячеек, с удалением двух противоположных граней из каждой и соединением наборов из шести вместе вокруг безликого куба ).
- Муоктаэдр : {6,4 | 4}: 4 шестиугольника на вершине (относящиеся к усеченным кубическим сотам , построенным из усеченного октаэдра с удаленными квадратными гранями и соединяющими пары отверстий вместе).
- Мутетраэдр : {6,6 | 3}: 6 шестиугольников на вершине (связанных с четвертью кубическими сотами , построенными из усеченных ячеек тетраэдра , удалением треугольных граней и соединением четырехугольников вокруг безликого тетраэдра ).
Кокстер дает эти правильные косые апейроэдры {2q, 2r | p} с расширенной киральной симметрией [[( p , q , p , r )] + ], которые, по его словам, изоморфны его абстрактной группе (2 q , 2 r | 2, p ). Соответствующие соты имеют расширенную симметрию [[( p , q , p , r )]]. [2]
Симметрия группы Кокстера | Апейроэдр {p, q | l} | Изображение | Лицо {p} | Отверстие { l } | Фигура вершины | Связанные соты | |
|---|---|---|---|---|---|---|---|
[[4,3,4]] [[4,3,4] + ] | {4,6 | 4} Мукубе |  анимация |  |  | 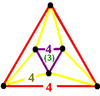 | т 0,3 {4,3,4} |  |
| {6,4 | 4} Муоктаэдр |  анимация |  | 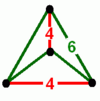 | 2т {4,3,4} | |||
[[3 [4] ]] [[3 [4] ] + ] | {6,6 | 3} Мутетраэдр | анимация | q {4,3,4} | ||||
Правильные косые апейроэдры в трехмерном гиперболическом пространстве [ править ]
В 1967 году К.В.Л. Гарнер идентифицировал 31 гиперболический косой апейроэдр с правильными косо-многоугольными вершинными фигурами , найденный в результате поиска, аналогичного трем вышеупомянутым, из евклидова пространства. [3]
Они представляют собой 14 компактных и 17 паракомпактных правильных косых многогранников в гиперболическом пространстве, построенных из симметрии подмножества графов линейных и циклических групп Кокстера вида [[( p , q , p , r )]]. Они определяют правильные косые многогранники {2 q , 2 r | p } и двойственное {2 r , 2 q | p }. Для частного случая групп линейных графов r = 2 это представляет группу Кокстера [ p , q , p ]. Он генерирует регулярные перекосы {2 q ,4 | p } и {4,2 q | p }. Все они существуют как подмножество граней выпуклых однородных сот в гиперболическом пространстве .
Косой апейроэдр имеет ту же фигуру вершины антипризмы, что и сот, но реализованы только зигзагообразные грани вершины фигуры, в то время как другие грани образуют «дыры».
| Группа Кокстера | Апейроэдр {p, q | l} | Лицо {p} | Отверстие {l} | Соты | Фигура вершины | Апейроэдр {p, q | l} | Лицо {p} | Отверстие {l} | Соты | Фигура вершины | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[3,5,3] | {10,4 | 3} | 2т {3,5,3} | {4,10 | 3} | т 0,3 {3,5,3} | |||||||
[5,3,5] | {6,4 | 5} | 2т {5,3,5} | {4,6 | 5} | т 0,3 {5,3,5} | |||||||
[(4,3,3,3)] | {8,6 | 3} | ct {(4,3,3,3)} | {6,8 | 3} | ct {(3,3,4,3)} | |||||||
[(5,3,3,3)] | {10,6 | 3} | ct {(5,3,3,3)} | {6,10 | 3} | ct {(3,3,5,3)} | |||||||
[(4,3,4,3)] | {8,8 | 3} | ct {(4,3,4,3)} | {6,6 | 4} | ct {(3,4,3,4)} | |||||||
[(5,3,4,3)] | {8,10 | 3} | ct {(4,3,5,3)} | {10,8 | 3} | ct {(5,3,4,3)} | |||||||
[(5,3,5,3)] | {10,10 | 3} | ct {(5,3,5,3)} | {6,6 | 5} | ct {(3,5,3,5)} |
| Группа Кокстера | Апейроэдр {p, q | l} | Лицо {p} | Отверстие {l} | Соты | Фигура вершины | Апейроэдр {p, q | l} | Лицо {p} | Отверстие {l} | Соты | Фигура вершины | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[4,4,4] | {8,4 | 4} | 2т {4,4,4} | {4,8 | 4} | т 0,3 {4,4,4} | |||||||
[3,6,3] | {12,4 | 3} | 2т {3,6,3} | {4,12 | 3} | т 0,3 {3,6,3} | |||||||
[6,3,6] | {6,4 | 6} | 2т {6,3,6} | {4,6 | 6} | т 0,3 {6,3,6} | |||||||
[(4,4,4,3)] | {8,6 | 4} | ct {(4,4,3,4)} | {6,8 | 4} | ct {(3,4,4,4)} | |||||||
[(4,4,4,4)] | {8,8 | 4} | q {4,4,4} | |||||||||
[(6,3,3,3)] | {12,6 | 3} | ct {(6,3,3,3)} | {6,12 | 3} | ct {(3,3,6,3)} | |||||||
[(6,3,4,3)] | {12,8 | 3} | ct {(6,3,4,3)} | {8,12 | 3} | ct {(4,3,6,3)} | |||||||
[(6,3,5,3)] | {12,10 | 3} | ct {(6,3,5,3)} | {10,12 | 3} | ct {(5,3,6,3)} | |||||||
[(6,3,6,3)] | {12,12 | 3} | ct {(6,3,6,3)} | {6,6 | 6} | ct {(3,6,3,6)} |
См. Также [ править ]
- Косой апейроэдр
- Правильный косой многогранник
Ссылки [ править ]
- ↑ Симметрия вещей, 2008, Глава 23 Объекты с первичной симметрией , Бесконечные платоновые многогранники , стр. 333–335
- ^ Кокстер, Правильные и полурегулярные многогранники II 2.34)
- ^ Гарнер, CWL Правильные косые многогранники в трехмерном гиперболическом пространстве. Может. J. Math. 19, 1179–1186, 1967. [1] Примечание: в его статье говорится, что их 32, но один самодуальный, остается 31.
- Пересмотренные карты Петри – Кокстера PDF , Изабель Хубард, Эгон Шульте, Азия Ивич Вайс, 2005 г.
- Джон Х. Конвей , Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 ,
- Питер МакМаллен , Четырехмерные правильные многогранники , Дискретная и вычислительная геометрия, сентябрь 2007 г., том 38, выпуск 2, стр. 355–387
- Кокстер , Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8
- Калейдоскопы: Избранные сочинения HSM Coxeter , отредактированные Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [2]
- (Бумага 2) HSM Coxeter, "Правильные губки или косые многогранники", Scripta Mathematica 6 (1939) 240–244.
- (Документ 22) HSM Кокстер, Регулярные и полурегулярные многогранники I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Документ 23) HSM Кокстер, Правильные и полурегулярные многогранники II , [Math. Zeit. 188 (1985) 559–591]
- Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги, Proceedings of the London Mathematics Society, Ser. 2 , Том 43, 1937 г.)
- Кокстер, HSM Правильные косые многогранники в трех и четырех измерениях. Proc. Лондонская математика. Soc. 43, 33–62, 1937.